
Flächenberechnung mit Integralrechnung, lineare Funktion
Ich zeige an einem Beispiel, wie man die Fläche unter einer linearen Funktion mit den Werten der Funktion berechnen kann. Dadurch kommt man auf eine Flächenfunktion. Wenn man diese Flächenfunktion F(x) integriert, ergibt sich F'(x) und das ist gleich der

Integral Regeln, Stammfunktion bilden
Der Exponent wird um eins erhöht. Die Potenzfunktion wird durch den neuen Exponenten dividiert. Anhand eines Beispiels erkläre ich, warum man hinter F(x) immer ein C setzen muss. Das könnt ihr hier nachlesen: https://123mathe.de/integral-flaechenfunktion

Bestimmtes Integral Flächenberechnung
0:00 Das bestimmte Integral hat Grenzen, das unbestimmte bildet alle Stammfunktionen 1:53 Beispiel berechnen: F(b)-F(a) = bestimmtes Integral 4:47 Beispiel berechnen: Fläche mit Integral Alle drei Teile gibt es auch in einzelnen Videos. Das könnt ihr hier
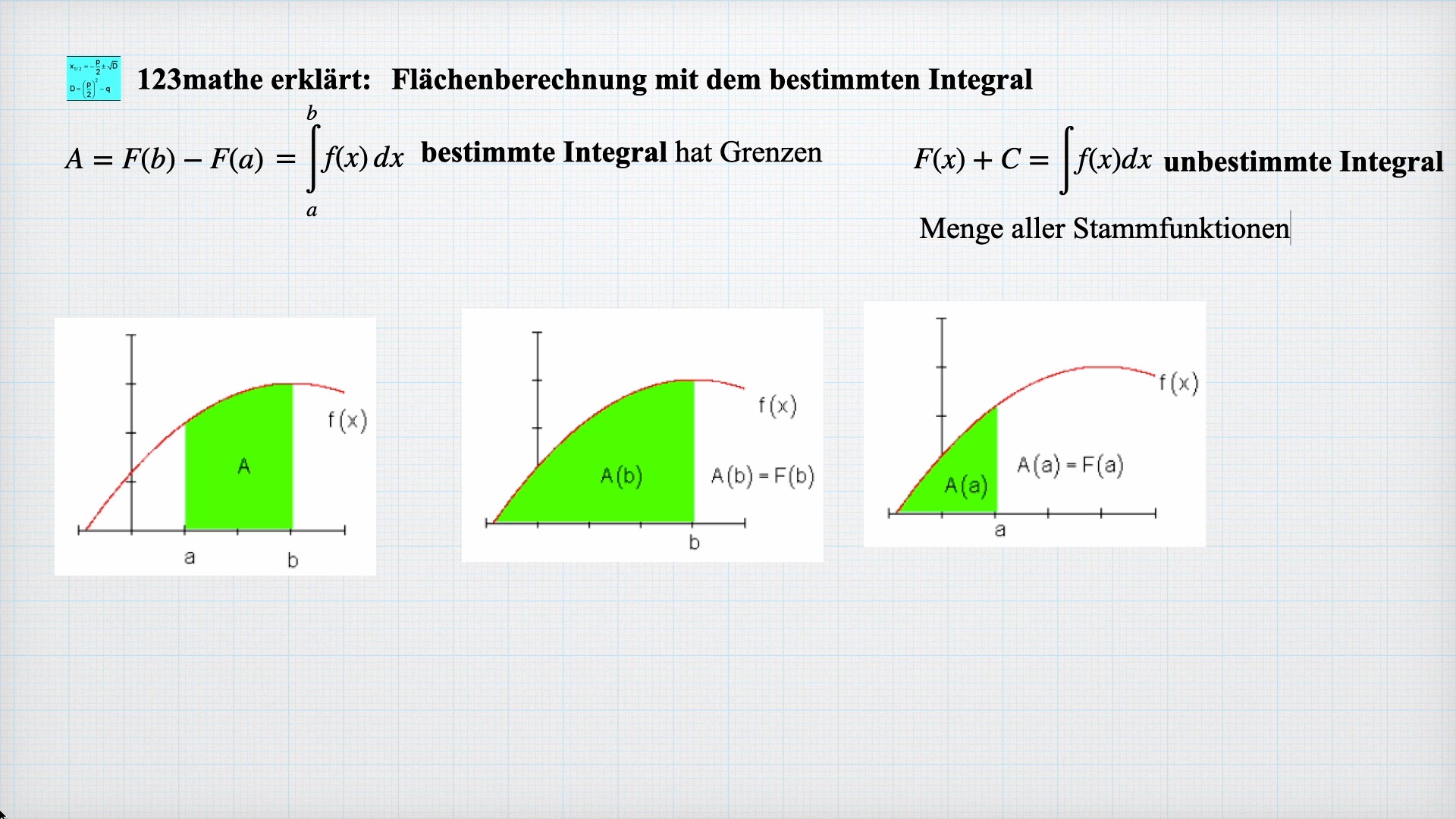
Bestimmtes unbestimmtes Integral
Anhand eines Graphen erkläre ich den Unterschied zwischen unbestimmtem und bestimmten Integral. Das ist der erste Teil des Videos Bestimmtes Integral Flächenberechnung. Das könnt ihr hier nachlesen: https://123mathe.de/vom-unbestimmten-zum-bestimmten-int

Bestimmtes Integral mit F(x) berechnen
Man kann die Fläche unter einem Funktionsgraphen als Subtraktion zweier Flächen berechnen. Also F(b) - F(a). Zuerst die Funktion integrieren, dann beide Werte einsetzen und subtrahieren. Dadurch fällt C weg. Das ist der zweite Teil des Videos Bestimmtes

Bestimmtes Integral mit F(x) berechnen
Man kann die Fläche unter einem Funktionsgraphen als Subtraktion zweier Flächen berechnen. Also F(b) - F(a). Zuerst die Funktion integrieren, dann beide Werte einsetzen und subtrahieren. Dadurch fällt C weg. Das ist der zweite Teil des Videos Bestimmtes

Bestimmtes Integral mit F(x) berechnen
Man kann die Fläche unter einem Funktionsgraphen als Subtraktion zweier Flächen berechnen. Also F(b) - F(a). Zuerst die Funktion integrieren, dann beide Werte einsetzen und subtrahieren. Dadurch fällt C weg. Das ist der zweite Teil des Videos Bestimmtes

Bestimmtes Integral berechnen
Man kann die Fläche unter einem Funktionsgraphen als Integral berechnen. Zuerst die Funktion integrieren, dann beide Werte einsetzen und subtrahieren. Das ist der dritte Teil des Videos Bestimmtes Integral Flächenberechnung. Das könnt ihr hier nachlese

Bestimmtes Integral berechnen
Man kann die Fläche unter einem Funktionsgraphen als Integral berechnen. Zuerst die Funktion integrieren, dann beide Werte einsetzen und subtrahieren. Das ist der dritte Teil des Videos Bestimmtes Integral Flächenberechnung. Das könnt ihr hier nachlese

Bestimmtes Integral berechnen
Man kann die Fläche unter einem Funktionsgraphen als Integral berechnen. Zuerst die Funktion integrieren, dann beide Werte einsetzen und subtrahieren. Das ist der dritte Teil des Videos Bestimmtes Integral Flächenberechnung. Das könnt ihr hier nachlese
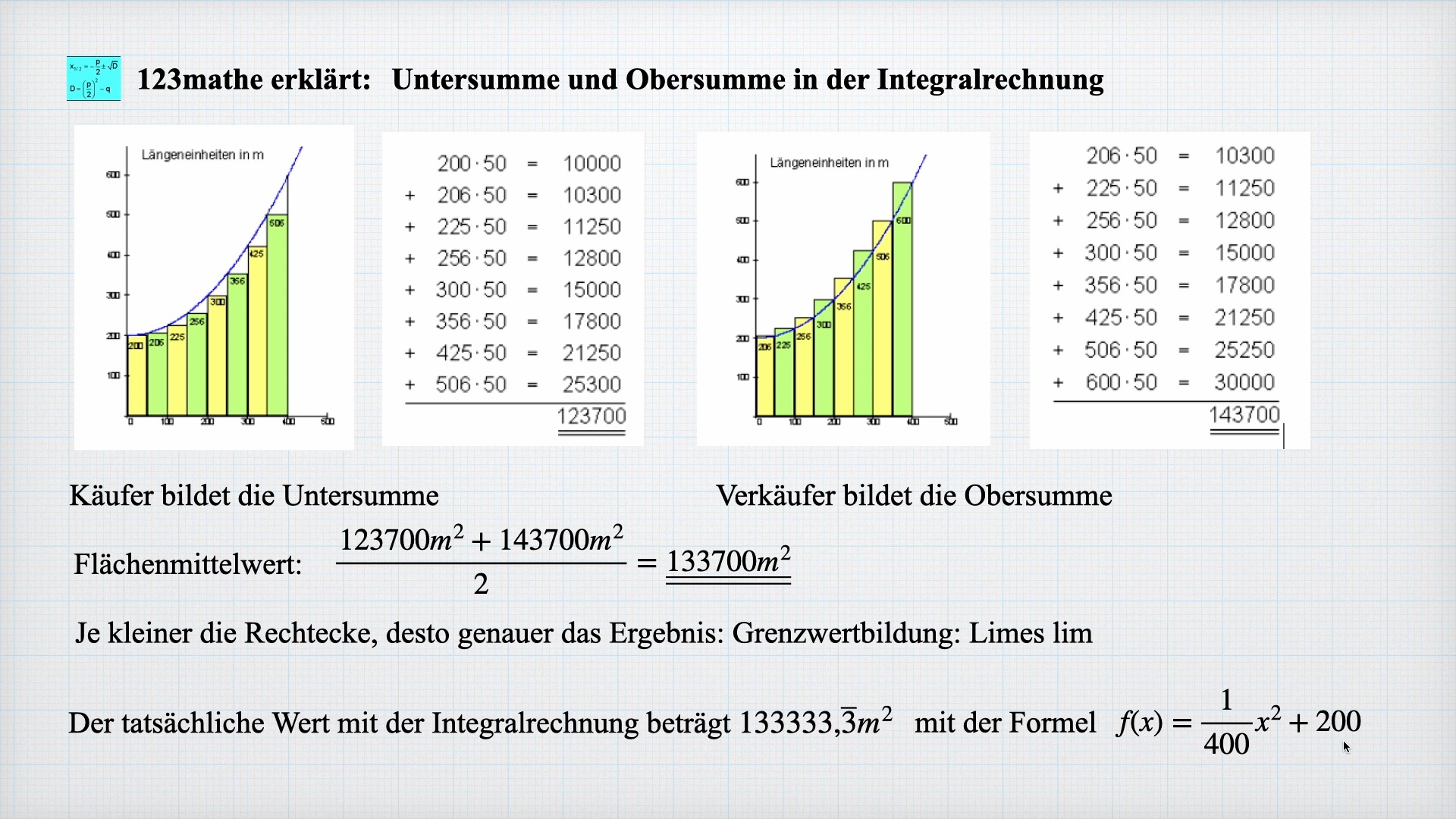
Untersumme Obersumme Integralrechnung
Zur Einführung in die Integralrechnung erkläre ich anhand eines krummen Grundstückes, wie man die Untersumme und Obersumme bildet. Aus beiden Ergebnissen kann man den Mittelwert bilden. Je kleiner die Rechtecke sind, in die man das Grundstück unterteilt,

Untersumme Obersumme Integralrechnung
Zur Einführung in die Integralrechnung erkläre ich anhand eines krummen Grundstückes, wie man die Untersumme und Obersumme bildet. Aus beiden Ergebnissen kann man den Mittelwert bilden. Je kleiner die Rechtecke sind, in die man das Grundstück unterteilt,

Fläche unter x-Achse Integralrechnung
0:00 Fläche oberhalb, Integral berechnen 1:33 Fläche unterhalb 2:17 FE>0: oberhalb; FE<0: unterhalb 2:36 Nur bis zu Nullstellen berechnen, Betrag bilden und Flächen addieren Das könnt ihr hier nachlesen: https://123mathe.de/flaechenberechnung-mittels-inte

Integral Fläche zwischen Graphen
0:00 Fläche zwischen zwei Funktionsgraphen = Fläche zwischen x-Achse und der 1. Funktion - Fläche zwischen x-Achse und der 2. Funktion. Jeweils mit den Integrationsgrenzen der Schnittpunkte der der Funktionen 1:16 1. x-Koordinaten der Schnittpunkte bestim
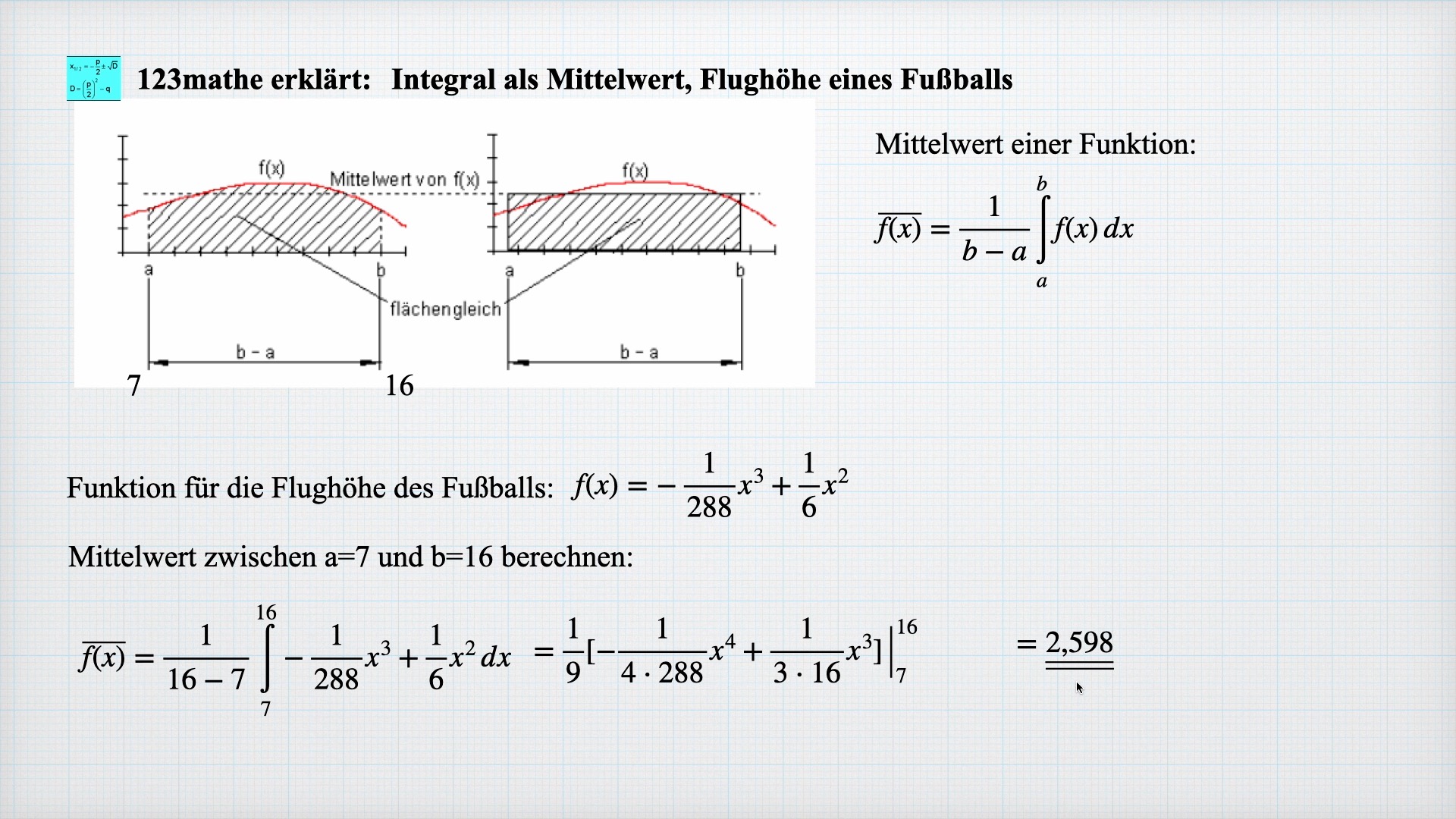
Integral als Mittelwert
Man kann den Mittelwert einer Funktion zwischen den x-Werten a und b berechnen, indem man das Integral der Funktion zwischen diesen Grenzen berechnet und durch b-a dividiert. 0:00 Mittelwert über konkrete Daten 1:33 Mittelwert über das Integral Das könnt