
Verknüpfung von Ereignissen in der Wahrscheinlichkeitsrechnung
Jul 12, 2024
Wenn zwei Ereignisse A und B mit und verknüpft werden, enthält die neue Schnittmenge C die Elemente, die in A und B enthalten sind. Wenn zwei Ereignisse A und B mit oder verknüpft werden, enthält die neue Vereinigungsmenge C die Elemente, die in A oder B

Ereignis und Gegenereignis Beispiele
Jun 17, 2024
Wenn ihr wissen wollt, wie man Gegenereignisse aufstellt, schaut euch viele Beispiele dazu an! Im vorherigen Video habe ich zwei erklärt. Hier seht ihr drei weitere. Das könnt ihr hier nachlesen: https://123mathe.de/ereignisse-in-der-wahrscheinlichkeitsre

Ereignis und Gegenereignis
Jun 17, 2024
Am besten stellt man erst die Ergebnismenge auf. Wenn man einen Würfel einmal wirft z. B. 1 bis 6. Danach schreibt man auf, welche Elemente davon auf das Ereignis A zutreffen. Z. B. Zahl ≤ 4. Alle Elemente der Ergebnismenge, die nicht auf das Ereignis A
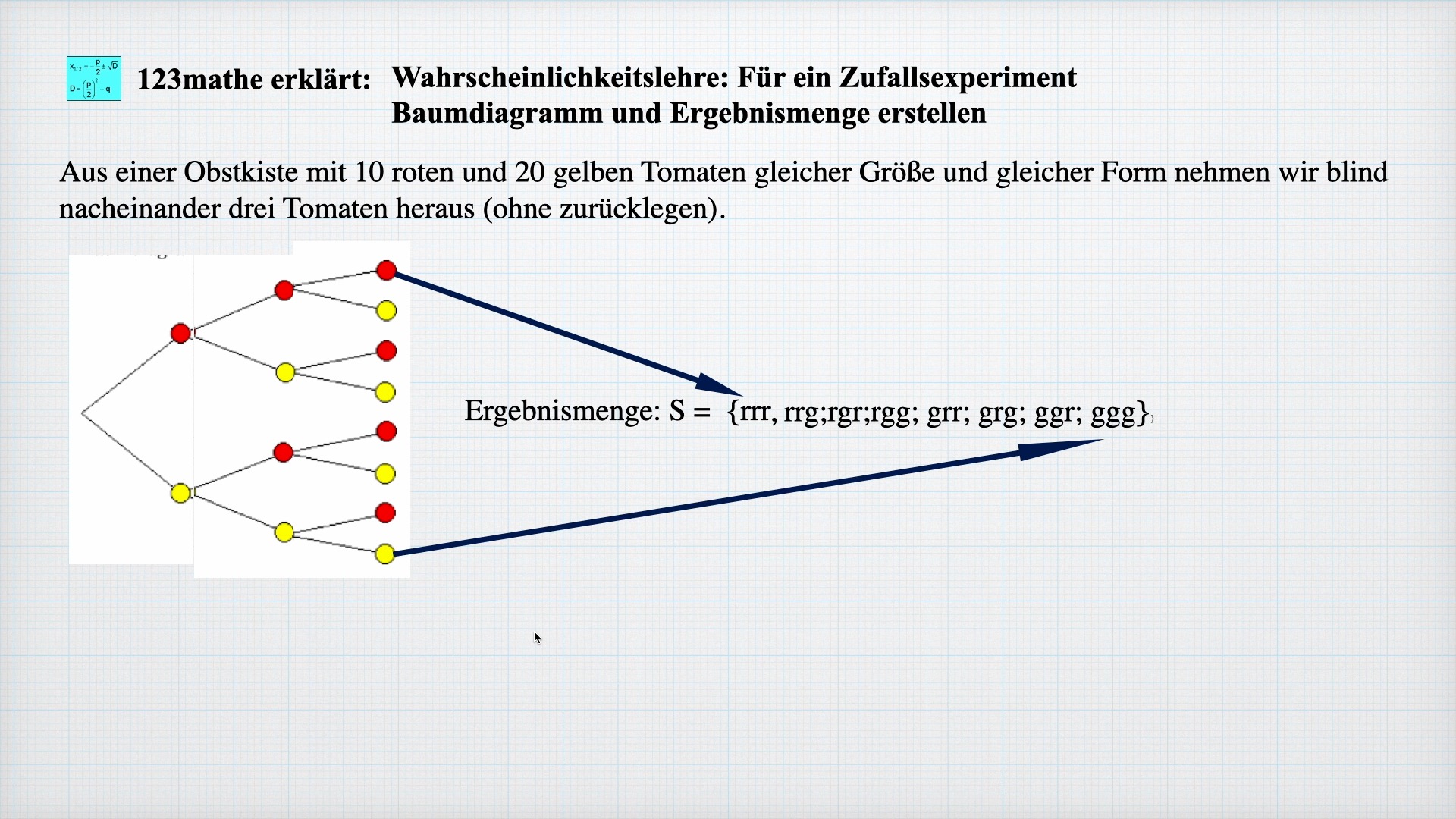
Baumdiagramm Ergebnismenge
Jun 14, 2024
Jedes Mal, wenn wir eine Tomate ziehen, gibt es zwei Möglichkeiten: rot oder gelb. Deshalb verzweigt sich das Baumdiagramm jedesmal, wenn wir ziehen. Die Ergebnismenge zählt auf, welche Möglichkeiten wir bei einem Durchgang haben. 0:00 Baumdiagramm 1:00 E

Wahrscheinlichkeit-verknüpfte
May 9, 2025
Ich erkläre anhand eines einfachen Beispiels, wie man die Wahrscheinlichkeit zweier Ereignisse berechnet, die mit oder verknüpft sind. Denn die beiden Ereignisse können sich überschneiden, deshalb darf man diese gemeinsamen Ereignisse nicht doppelt berück

Wahrscheinlichkeit abhängig? berechnen
May 26, 2025
Ich zeige anhand eines einfachen Beispiels, wie man berechnet, ob zwei Eigenschaften voneinander abhängig sind. Wir erstellen zuerst die Vierfeldertafel, daraus zwei Ereignisbäume. Dann berechnen wir P(A | B) und tragen dies ein. Wenn wir sehen, dass P(A)
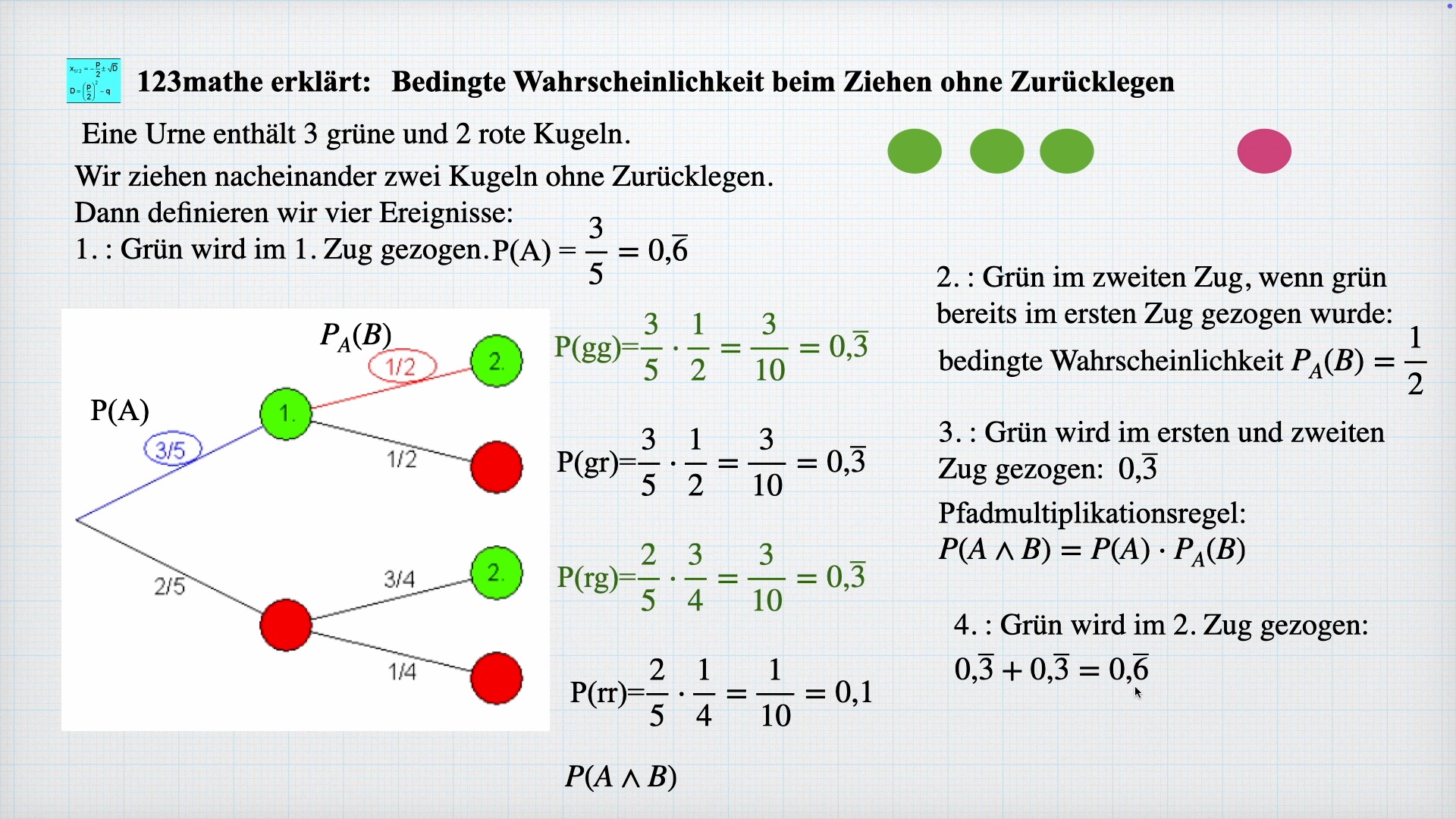
Bedingte Wahrscheinlichkeit ohne Zurücklegen
May 15, 2025
Ich erkläre anhand eines einfachen Beispiels, wie man die bedingte Wahrscheinlichkeit beim Ziehen ohne Zurücklegen für folgendes berechnet: A: Grün wird im 1. Zug gezogen, P(A). B: Grün wird im 2. Zug gezogen, P(B) unter der Bedingung von A. C: Grün wird
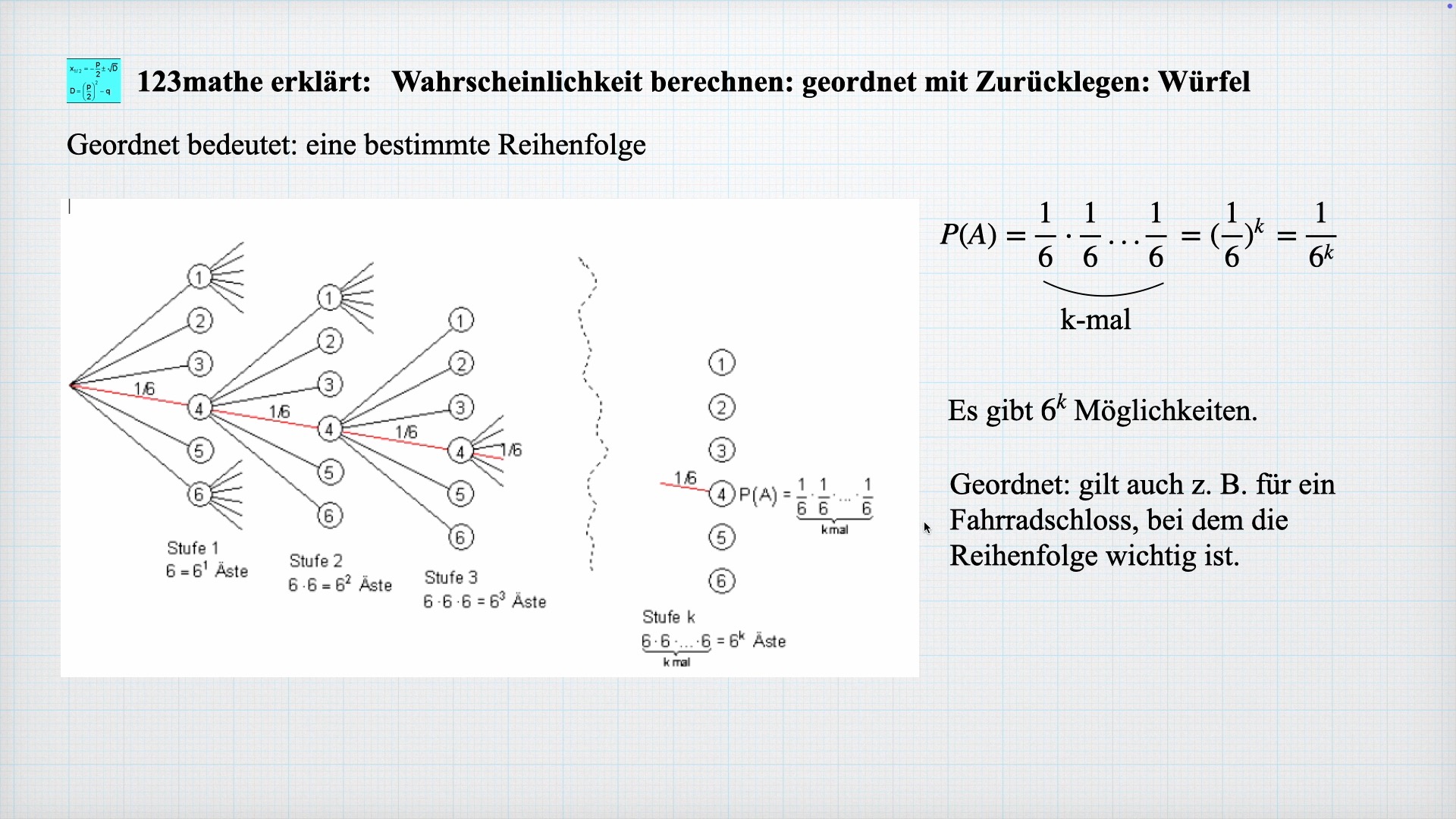
Wahrscheinlichkeit berechnen mit Zurücklegen
May 27, 2025
Ich erkläre wie man die Wahrscheinlichkeit berechnet, wenn die die Stichprobe geordnet und zurückgelegt wird. Wenn man z. B. mehrmals eine 4 würfelt, kommt das Baumdiagramm an seine Grenzen. Das könnt ihr hier nachlesen: https://123mathe.de/kombinatorik