Physik Klasse 9
- In diesem Beitrag erkläre ich als erstes, dass Geschwindigkeit ein Bezugssystem braucht.
- Dann stelle ich die Arten von Geschwindigkeit vor.
- Danach führen wir in Gedanken einen Versuch mit gleichförmiger Geschwindigkeit durch.
- Für die Auswertung brauchen wir die Variablen Stecke, Zeit und Beschleunigung.
- Die Ergebnisse tragen wir in einer Messtabelle, im Weg-Zeit-Diagramm und im Geschwindigkeits-Zeit-Diagramm ein.
- Dann stelle ich die Geschwindigkeitsformel um, so dass wir auch die Strecke und die Zeit berechnen können.
- Damit ihr wisst, welche Formel ihr wann braucht, habe ich ein paar Tipps zum Berechnen der Aufgaben gegeben.
- Zum Schluss zeige ich, wie man Kilometer pro Stunde in Meter pro Sekunde umrechnen kann.
Geschwindigkeit braucht ein Bezugssystem
- Ich sitze im Zug, der auf dem Bahnhof steht. Auf dem Bahnsteig gegenüber steht ebenfalls ein Zug. Einer der beiden Züge fährt an. Welcher ist es?
- Dann laufe ich in einem mit Tempo 100 fahrenden Zug. Mit welcher Geschwindigkeit bewege ich mich?
- Ich laufe auf der Rolltreppe. Meine Geschwindigkeit gegenüber der Umgebung ist eine andere als gegenüber der Treppe.
Um eine klare Aussage über die jeweilige Geschwindigkeit zu machen, brauche ich einen Punkt oder Gegenstand auf den ich mich beziehe. Dazu führt der Physiker ein Bezugssystem ein. Bezugssysteme sind frei wählbar. Es können sein: Der Labortisch, der Fußboden, die Erdoberfläche, die Sonne, die Milchstraße usw.
Arten von Geschwindigkeiten:
Bei einer verzögerten Bewegung nimmt die Geschwindigkeit ab.
Bei einer beschleunigten Bewegung nimmt die Geschwindigkeit dagegen zu.
Hat ein Körper eine konstante Geschwindigkeit, so ist die Bewegung gleichförmig. Also in der gleichen Zeiten werden gleich große Wegstrecken zurückgelegt. In der Physik sagt man auch: Der zurückgelegte Weg ist der dafür benötigten Zeit proportional. Der Quotient „Weg durch Zeit“ ist somit konstant.
Mit dieser beschäftigen wir uns in diesem Beitrag.
Wendet man diese Gleichung auf Bewegungen an, die nicht gleichförmig sind, so erhält man die Durchschnittsgeschwindigkeit.
Versuch zur Bewegung mit gleichbleibender Geschwindigkeit
Wir lassen ein Spielzeugauto mit gleichförmiger Bewegung über den Tisch fahren. Dabei messen wir mit einer Stoppuhr die Zeit für eine bestimmte Strecke. Die gemessenen Werte listen wir dann in einer Tabelle auf.
Variablen Strecke, Zeit und Geschwindigkeit
Dabei arbeiten wir mit folgenden Variablen:
s : steht für die Strecke in m Metern. s/m bedeutet also Strecke in Metern
t : steht für die Zeit in s Sekunden. t/s bedeutet also Zeit in Sekunden.
Daraus errechnen wir:
v : die Geschwindigkeit, also s/t : Strecke dividiert durch Zeit.
Die Basiseinheit zur Messung der Geschwindigkeit ist Meter pro Sekunde (\frac{m}{s} ).
Im alltäglichen Sprachgebrauch wird aber oft die Einheit Kilometer pro Stunde (\frac{km}{h} ) verwendet.
Wir messen die Strecke, die unser Wagen zurück gelegt hat, alle 2 Sekunden, berechnen die Geschwindigkeit und tragen die Ergebnisse in einer Messtabelle ein:
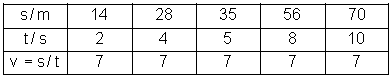
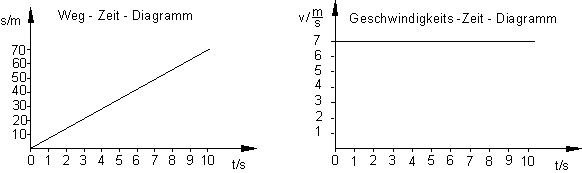
Die Werte der Tabelle können wir anschließend graphisch in einem Weg-Zeit-Diagramm darstellen. Das heißt, auf der x-Achse tragen wir die Zeit in Sekunden ein, auf der y-Achse den Weg in Metern. Dabei sehen wir, dass die Steigung des Graphen gleichförmig ist.
Oder wir nutzen ein Geschwindigkeits-Zeit-Diagramm. Hierbei tragen wir auf der x-Achse die Zeit in Sekunden ein, auf der Y-Achse die Geschwindigkeit v in m/s, also in Metern pro Sekunde.
Formeln:
Geschwindigkeit berechnen:
Wir brauchen uns nur die Formel Geschwindigkeit v = s/t, also Strecke durch Zeit, zu merken.
Strecke berechnen:
Wenn wir die Geschwindigkeit und die Zeit eines Objekts kennen, können wir auch die Strecke errechnen. Dazu müssen wir die Formel nur umstellen. Dazu multiplizieren wir auf beiden Seiten mit t und erhalten Strecke s = v * t.
Zeit berechnen:
Wenn wir die Geschwindigkeit und die Strecke kennen, dividieren wir die Formel durch v und erhalten die Zeit: t = s/v.

Tipp: Welche Formel braucht man?
Bei Textaufgaben ist es immer hilfreich, sich folgendes klar zu machen:
Was ist gegeben? Mit anderen Worten: Welche Informationen haben wir? Wenn in den Aufgaben z. B. Entfernungen angeben werden, haben wir die Strecke. Das steht dann rechts in der Berechnung.
Was ist gesucht? Mit anderen Worten: Was sollen wir berechnen? Wenn z. B. nach einer Entfernung gefragt wird, brauchen wir die Formel, um eine Strecke zu berechnen. Dann kennen wir
die Geschwindigkeit und die Zeitangabe.
Also bei Textaufgaben zuallerst überlegen: Welche Informationen haben wir und welche sollen wir berechnen?
Umrechnung Kilometer pro Stunde in Meter pro Sekunde
Bis jetzt haben wir die Geschwindigkeit in Meter pro Sekunde = m/s berechnet. Jetzt wollen wir dies in Kilometer pro Stunde = km/h umrechnen. Dazu müssen wir nur wissen, dass 1 km = 1000 m und 1 h = 3600 s.
Also ist 1 \frac{km}{h} = 1000 \frac{m}{3600s} = 0,2777 \frac{m}{s} .
Entsprechend müssen wir vorgehen, wenn wir Meter pro Sekunde in Kilometer pro Stunde umrechnen wollen:
1 \frac{m}{s} = \frac{0,001 km}{0,002777 h} = 3,6 \frac{km}{h} .
Wie man Meter pro Sekunde \dfrac{m}{s} in Kilometer pro Stunde \dfrac{km}{h} umrechnet, zeigen wir in diesem 📽 Video m/s in km/h umrechnen!
Jetzt können wir die 2. Aufgabe in Aufgaben zur gleichförmigen Bewegung berechnen! Viel Erfolg!
Hier findest du eine Übersicht über weitere Beiträge zum Thema Mechanik und Elektronik, darin auch Links zu Aufgaben.