Zuerst definiere ich Sinuskurven und Sinusschwingungen. Danach führe ich einen Versuch zu Schwingungen durch. Anschließend gebe ich die physikalische Definition periodischer Bewegungen und die Definition und Formel zur Frequenz. Dann erkläre ich das Kraftgesetz der harmonischen Schwingung und untersuche es am Federpendel. Nachdem ich auf die Winkelgeschwindigkeit eingegangen bin, leite ich die Schwingungsgleichung ab. Zum Schluss gehe ich auf die Periodendauer eines Fadenpendels ein.
Definitionen Sinuskurve und Sinusschwingung
Eine Stimmgabel erzeugt einen Ton. Ihre Zinken zeigen dabei eine besonders gleichmäßige Hin- und Herbewegung. Deren Aufzeichnung ergibt eine Sinuskurve. Eine solche Schwingung nennen wir in der Physik deshalb Sinusschwingung oder harmonische Schwingung.
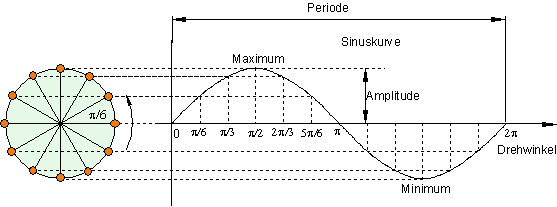
Beschreibung von Schwingungen
Versuch
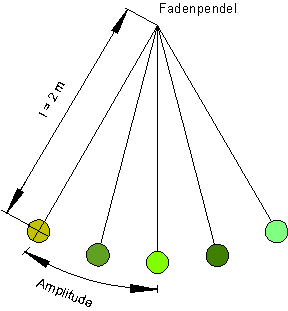
Wir beobachten die Bewegung eines Fadenpendels.
Danach lenken wir die Kugel aus und lassen sie los. Dann führt sie eine sich ständig wiederholende Hin – und Herbewegung aus.
Physikalische Definition periodische Bewegung
Eine solche Bewegung heißt periodische Bewegung.
Eine vollständige Hin – und Herbewegung der Pendelkugel nennen wir eine Periode.
Die Zeit, in der das Pendel eine Periode ausführt, heißt daher Periodendauer T.
Während jeder Hin- und Herbewegung schwingt die Pendelkugel zum selben Umkehrpunkt und hat dort ihre größte Auslenkung.
Die Auslenkung von der Mittellage zum Umkehrpunkt nennen wir Amplitude der Schwingung.
Frequenz Definition und Formel
Die Anzahl der Perioden pro Sekunde heißt Frequenz f.
![]()
Versuch
Wir lenken ein Fadenpendel mit derPendellänge l = 2 m um 40 cm aus und messen die Zeit T für eine Periode.
Anschließend bestimmen wir die Zeit für n = 10 Schwingungen t = 28 s.
Die Periodendauer beträgt 28 s/10 = 2,8 s.
Danach wiederholen wir den Versuch mit der halben Amplitude 20 cm.
Die Periodendauer beträgt wieder 2,8 s.
Anschließend wiederholen wir den Versuch bei kürzeren Pendellängen.
Die Ergebnisse schreiben wir dann in eine Tabelle.
Schließlich berechnen wir die Frequenz f = n/t
| Pendellänge l in m | 2 | 1 | 0,5 | 0,25 |
| Anzahl der Schwingungen n | 10 | 10 | 10 | 10 |
| Zeit t für n Schwingungen in s | 28 | 20 | 14 | 10 |
| Periodendauer T = t/n in s | 2,8 | 2 | 1,4 | 1 |
| Frequenz f = n/t in Hz | 0,36 | 0,5 | 0,71 | 1 |
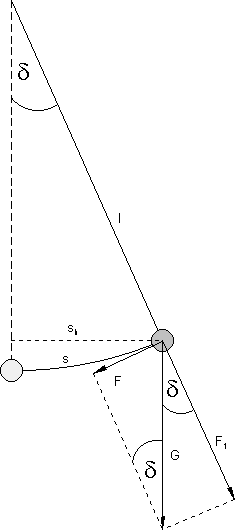
Kraftgesetz der harmonischen Schwingung
Untersuchung am Federpendel
a) In der Gleichgewichtslage hebt die nach oben gerichtete (positive) Zugkraft F0 der Feder die nach unten gerichtete (negative) Gewichtskraft G gerade auf.
Es gilt G = – F0.
Also ist die Gesamtkraft F = G + F0 = 0
b) Nun wird der Körper um die Strecke s > 0 nach oben ausgelenkt. Dann verkleinert sich die nach oben wirkende Zugkraft der Feder auf F1 = F0 – D s. Die Gewichtskraft überwiegt. Es ergibt sich nach unten die resultierende Kraft:
F = G + F1 = G + F0 – D s = 0 – D s
c) Wenn man den Körper um die Strecke s < 0 nach unten auslenkt, vergrößert sich die nach oben wirkende Zugkraft der Feder auf F1 = F0 – D s. Beachte, dass hier s negativ, also – D s positiv ist. Jetzt überwiegt die Federkraft. Die resultierende Kraft nach oben ist:
F = G + F1 = G + F0 – D s = 0 – D s
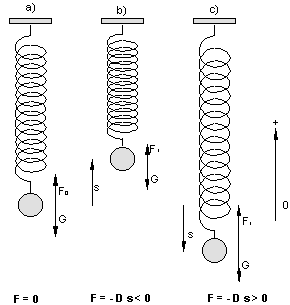
Die Rückstellkraft F ist also proportional zur Auslenkung s.
Es gilt das Elongation-Kraft-Gesetz:
Versuch
Wir befestigen einen Korken K‘ auf dem Rand einer vertikal gestellten drehbaren Scheibe. Die Drehzahl stellen wir dabei so ein, dass die Umlaufdauer des Korkens gleich der Periodendauer des Federpendels ist. In der Schattenprojektion entsteht dadurch ein vertikaler Strich, an dem der Korkenschatten auf und ab gleitet. Der Kugelschatten des Federpendels vollführt die gleiche Bewegung.
Während der Korken K‘ auf einem Kreis mit dem Radius r umläuft, pendelt die Kugel K auf der s – Achse um ihre Gleichgewichtslage s = 0. Diese liegt in der Mitte zwischen den beiden Umkehrpunkten s = A = r und s = – A = – r. Der positive Wert A heißt Amplitude der Schwingung. Sie ist die maximale Auslenkung aus der Gleichgewichtslage.
Für die Auslenkung s gilt:
Das entspricht einer harmonischen Schwingung.
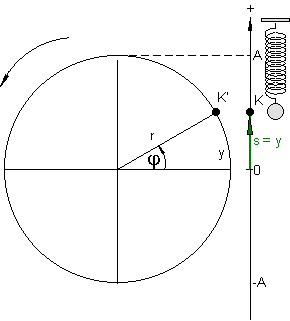
Die Winkelgeschwindigkeit

Herleitung der Schwingungsgleichung

Merke

Das Fadenpendel

Periodendauer eines Fadenpendels
Ein Fadenpendel schwingt bei hinreichend kleiner Amplitude harmonisch.
Seine Periodendauer ist dann:
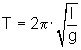
Bemerkung: Über die Periodendauer des Fadenpendels lässt sich sehr genau die Erdbeschleunigung g ermitteln.
Dazu muss die Fadenlänge und die Periodendauer gemessen werden.
Hier finden Sie Aufgaben zur harmonischen Schwingung I.
Und hier eine Übersicht über weitere Beiträge aus der Oberstufenphysik.