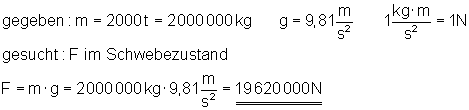Hier findest du die Lösungen der Aufgaben zur Beschleunigung mit Masse und Kraft.
1. Wie groß ist die Kraft?
Ein Auto der Masse m = 1100 kg erfährt beim Start eine Beschleunigung von a = 5 m/s2.
Wie groß ist die Kraft, die das Auto in Bewegung setzt?
gegeben: m = 1110 kg, a = 5 \frac{m}{s^2}
gesucht: F
F = m \cdot a = 1100 kg \cdot 5 \dfrac{m}{s^2} = 5500 \dfrac{kg \cdot m}{s^2} = \underline{\underline{5500N}}
Das Auto wird mit einer Kraft von 5500 N in Bewegung gesetzt.
Diese Aufgabe habe ich in diesem Video Kraft aus Masse und Beschleunigung berechnen erklärt.
2. Welche Geschwindigkeit?
Bei einem Torschuss schießt ein Spieler den Fußball mit der Masse m = 0,5 kg mit einer Schusskraft von F = 500 N aufs Tor.
Welche Geschwindigkeit erreicht der Fußball, wenn das Abschießen etwa 0,02 s dauert?
Anleitung: Berechne zuerst die Beschleunigung, die der Fußball erfährt. Bestimme dann die Geschwindigkeit für die beschleunigte Bewegung.
gegeben: m = 0,5kg , F = 500N , t = 0,02s
gesucht: v
F = m \cdot a \Rightarrow a = \frac{F}{m}
v = a \cdot t = \frac{F}{m} \cdot t = \frac{500kg \cdot \frac{m}{s^2}}{0,5kg} \cdot 0,02s = \underline{\underline{20 \frac{m}{s}}}
Der Fußball erreicht eine Geschwindigkeit von 20 m/s.
3. Welche Kraft ist nötig?
Welche Kraft ist nötig, um ein Auto der Masse m = 1000 kg in 10 s auf eine Geschwindigkeit von 20 m/s zu beschleunigen?
Anleitung: Berechne zuerst aus den gegebenen Größen die Beschleunigung. Wende dann zur Berechnung der Kraft das dynamische Grundgesetz an.
gegeben: m = 1000kg , t = 10s , v = 20 \frac{m}{s}
gesucht: F
F = m \cdot a
v = a \cdot t \Rightarrow a = \frac{v}{t}
\Rightarrow F = m \cdot \frac{v}{t} = 1000kg \cdot \frac{20 \frac{m}{s}}{10s} = \frac{1000 \cdot 20}{10} \cdot \frac{kg \cdot m}{s^2} = \underline{\underline{2000N}}
Zur Beschleunigung ist eine Kraft von 2000 N erforderlich.
4. Welche Kraft braucht man zum Beschleunigen?
Ein Zug der Masse m = 700 t fährt mit der Beschleunigung 0,15 m/s2 aus der Ruhe an.
Welche Kraft braucht man zum Beschleunigen?
gegeben: m = 700t = 700000kg , a = 0,15 \frac{m}{s^2}
gesucht: F
F = m \cdot a = 700000kg \cdot 0,15 \frac{m}{s^2} = 700000 \cdot 0,15 \frac{kgm}{s^2} = 105000N = \underline{\underline{105kN}}
Die Beschleunigungskraft beträgt 105 kN.
5. Kann man per Kanone zum Mond?
Im Roman von Jules Verne (Die Reise zum Mond) wurde die Mondrakete aus einer Kanone abgeschossen. Wäre das technisch möglich?
Daten:
Masse des menschlichen Körpers: m = 70 kg
Nötige Startgeschwindigkeit: v = 11 km/s
Länge des Kanonenrohres: s = 100 m
Diese Aufgabe habe ich in diesem 
gegeben: m = 70kg , v = 11 \frac{km}{s} , s = 100 m
gesucht: a \quad und \quad F
v = a \cdot t \Rightarrow t = \frac{v}{a}
\Rightarrow s = \frac{a}{2} t^2 = \frac{a}{2}( \frac{v}{a} )^2 = \frac{a \cdot v^2}{2 \cdot a^2} = \frac{v^2}{2a} \Rightarrow a = \color{red}{ \frac{v^2}{2s} }
F = m \cdot a = m \cdot \color{red}{\frac{v^2}{2s}} = 70kg \cdot \frac{ (11000 \frac{m}{s})^2 }{2 \cdot 100m} = \frac{70 \cdot (11000)^2}{200} \cdot kg \cdot \frac{ \frac{m^2}{s^2} }{m} = 42350000N = \underline{\underline{42,35MN}}
\Rightarrow a = \frac{F}{m} = \frac{42350000 \cdot \frac{kg \cdot m}{s^2}}{70kg} = \underline{\underline{605000 \frac{m}{s^2}}}
Der Beschleunigungswert beträgt 60 500 G, das hält weder Mensch, noch irgendein Material aus.
6. Ein Schlitten wird beschleunigt
Ein Schlitten, der zusammen mit einer darauf sitzenden Person die Masse 80 kg hat, wird mit der Kraft F = 50 N aus dem Stand beschleunigt.
I Berechne für den Fall, dass keine Reibungskräfte zu überwinden sind:
a) Die Beschleunigung, die der Schlitten erfährt.
b) Die Beschleunigungsstrecke, die in den ersten 4 Sekunden zurückgelegt wird.
c) Die erreichte Geschwindigkeit nach 4 Sekunden.
II Wiederhole obige Rechnung für den Fall, dass beim Ziehen des Schlittens eine konstante Reibungskraft FR = 10 N zu überwinden ist.
I. Rechnung ohne Reibungskräfte
a)
Lösung:
F = m \cdot a \Rightarrow a = \frac{F}{m} = \frac{50N}{80kg} = \frac{50kg \frac{m}{s^2}}{80kg} = \frac{50}{80} \frac{m}{s^2} = \underline{\underline{0,625 \frac{m}{s^2}}}
Der Schlitten erfährt eine Beschleunigung von a = 0,625 m/s2.
b)
s = \frac{a}{2}t^2 = \frac{0,625 \frac{m}{s^2}}{2} \cdot 16s^2 = \underline{\underline{5m}}
Die Beschleunigungsstrecke, in den ersten 4 Sekunden beträgt s = 5 m.
c)
v = a \cdot t = 0,625 \frac{m}{s^2} \cdot 4s = \underline{\underline{2,5 \frac{m}{s}}}
Die erreichte Geschwindigkeit nach 4 Sekunden beträgt v = 2,5 m/s.
II. Rechnung mit der konstanten Reibungskraft FR = 10 N
Beschleunigungskraft: F_{B} = F - F_{R} = 50N - 10N = 40N
a)
Lösung:
F = m \cdot a \Rightarrow a = \frac{F}{m} = \frac{40N}{80kg} = \frac{40kg \frac{m}{s^2}}{80kg} = \frac{40}{80} \frac{m}{s^2} = \underline{\underline{0,5 \frac{m}{s^2}}}
Der Schlitten erfährt eine Beschleunigung von a = 0,5 m/s2.
b)
s = \frac{a}{2} t^2 = \frac{0,5 \frac{m}{s^2}}{2} \cdot 16s^2 = \underline{\underline{4m}}
Die Beschleunigungsstrecke, in den ersten 4 Sekunden beträgt s = 4 m.
c)
v = a \cdot t = 0,5 \frac{m}{s^2} \cdot 4s = \underline{\underline{2,0 \frac{m}{s}}}
Die erreichte Geschwindigkeit nach 4 Sekunden beträgt v = 2 m/s.
7. Ein Auto beschleunigt
Ein Mittelklassewagen (Masse: 1000 kg) beschleunigt in 10 svon 0 auf 100 km/h.
a) Wie groß ist die mittlere Beschleunigung?
b) Wie groß die mittlere Kraft auf das Auto?
Ausführliche Lösungen:
gegeben: m = 1000kg , t = 10s , v = 100 \frac{km}{h} = \frac{100}{3,6} \frac{m}{s}
a)
Lösung:
v = a \cdot 7 \Rightarrow a = \frac{v}{t} = \frac{\frac{100}{3,6} \frac{m}{s}}{10s} = \color{red}{ \frac{10}{3,6} \frac{m}{s^2}} \approx \underline{\underline{2,7 \frac{m}{s^2}}}
b)
F = m \cdot a = 1000kg \cdot \color{red}{ \frac{10}{3,6} \frac{m}{s^2}} \approx 2777,7 \frac{kgm}{s^2} = \underline{\underline{2777,7N}}
8. Warum müssen die Kolben so leicht wie möglich sein?
Die Kolben eines Verbrennungsmotors werden aus Aluminium hergestellt, also aus einem sehr leichten Metall. Warum müssen die Kolben so leicht wie möglich sein?
Ausführliche Lösung
Da die Kolben bei einer hohen Motordrehzahl wie z.B. 6000 / min sich in der Sekunde 100 mal auf und ab bewegen, sind sie großen Beschleunigungskräften ausgesetzt. Um die dabei auftretenden Kräfte in den Lagern möglichst gering zuhalten, kann das wegen F = m x a nur über eine geringe Kolbenmasse erreicht werden.9.Beim Abschleppen eines Fahrzeugs besteht die Gefahr, dass das gespannte Zugseil durch ruckartiges Anfahren reißt. Begründe dies.
9. Ein Fahrzeug wird abgeschleppt
Beim Abschleppen eines Fahrzeugs besteht die Gefahr, dass das gespannte Zugseil durch ruckartiges Anfahren reißt. Begründe dies.
Ausführliche Lösung
Beim ruckartigen Anfahren können durch die Trägheit des abzuschleppenden Fahrzeugs so hohe Kräfte im Zugseil entstehen, dass es reißt.
10. Wie lautet der Trägheitssatz?
Wie lautet der Trägheitssatz? Weshalb kommt trotzdem ein antriebsloses Fahrzeug auf ebener gerader Strecke nach einer bestimmten Zeit zum Stillstand?
Ausführliche Lösung
Der Trägheitssatz von Galileo Galilei:
Ein Körper bleibt in Ruhe oder in gleichförmiger Bewegung, wenn keine Kraft auf ihn wirkt.
Das bedeutet, nur unter dem Einfluss einer Kraft kann ein Körper seinen Bewegungszustand ändern.
Ein antriebsloses Fahrzeug kommt auf einer ebenen Straße irgendwann zum Stillstand, weil es durch Reibungskräfte abgebremst wird (Fahrtwind, Lagerreibung).
11. Was besagt das Newtonsche Kraftgesetz?
Das Newtonsche Kraftgesetz:

12. Wie groß ist die Bremsverzögerung?
Ein Auto mit der Masse 1400 kg wird mit einer Bremskraft von 3,6 kN gebremst.
Wie groß ist die Bremsverzögerung?
Ausführliche Lösung
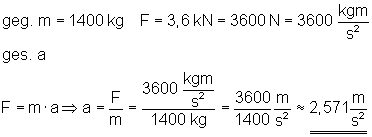
Die Bremsverzögerung beträgt etwa 2,571 m/s2.
13. Welche Kräfte müssen Kniee aushalten?
Welche durchschnittlichen Kräfte haben die Kniegelenke auszuhalten, wenn jemand von einer 2 m hohen Mauer herunterspringt? Gehe von einer Masse m = 70 kg, einer Bremsstrecke von 0,5 m und der Aufprallgeschwindigkeit 6,3 m/s aus.
Ausführliche Lösung

Die Kniegelenke haben Kräfte von F = 2778,3 N abzufangen.
14. Ein Flugzeugträger startet
Auf dem Flugzeugträger Nimitz können Flugzeuge bis zu einer Masse von 36000 kg mit dem Katapult gestartet werden. Dabei werden sie auf einer Strecke von 76 m auf eine Geschwindigkeit von 252 km/h gebracht.
a) Welche Kraft muss das Katapult ausüben?
b) Wie groß ist die Kraft im Verhältnis zur Gewichtskraft (F/G)?
c) Wie groß ist die Kraft, die auf den Piloten wirkt (m = 75 kg).
Ausführliche Lösung
a)
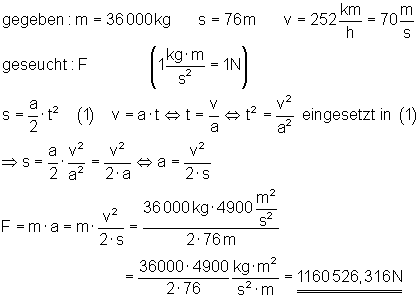
Das Katapult muss eine Kraft von 1 160 526,316 N ausüben.
b)
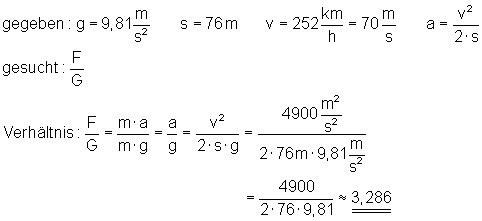
Das Verhältnis F/G beträgt etwa 3,286.
Das bedeutet, der Pilot wird bei dem Beschleunigungsvorgang mit dem 3,3-fachen seiner Gewichtskraft in den Sitz gepresst.
c)
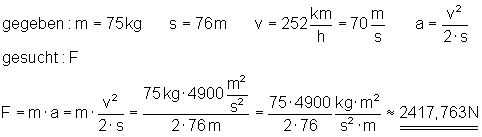
Auf den Piloten wirkt eine Kraft von 2417,763 N.
15. Das Spaceshuttel startet
Die Masse des Spaceshuttles beträgt beim Start zusammen mit der Trägerrakete 2000 t (2.000.000 kg).
a) Wie groß ist die Schubkraft, wenn die Rakete unmittelbar nach dem Start gerade schwebt?
b) Die tatsächliche Schubkraft der Rakete beträgt 30 MN (30.000.000 N).
Welche Beschleunigung kann der Rakete damit verliehen werden?
c) Wie lange benötigt die Rakete für den ersten Kilometer und welche Geschwindigkeit hat sie am Ende dieser Strecke erreicht?
d) Warum kann über eine längere Flugstrecke die Beschleunigung nicht mehr als konstant angenommen werden?
Ausführliche Lösung
a)
Die Schubkraft ist gleich der Gewichtskraft F = G = 19 620 000 N.
b)
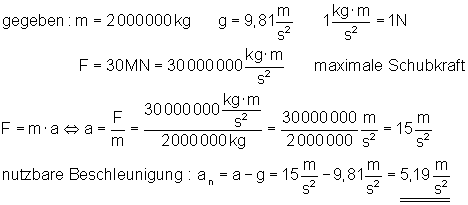
Der Rakete kann eine Beschleunigung von 5,19 m/s2 verliehen werden.
Da die Rakete senkrecht startet, muss der Antrieb auch die Erdbeschleunigung überwinden.
c)
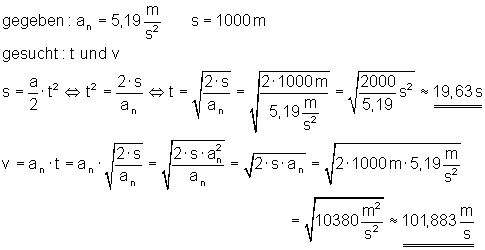
Für den ersten Kilometer benötigt die Rakete etwa 19,63 s.
Am Ende dieser Strecke hat sie eine Geschwindigkeit von etwa 101,882 m/s.
d)
Die Masse der Rakete nimmt ab, da Treibstoff verbraucht wird. Bei gleichbleibender Schubkraft würde sich dadurch die Beschleunigung erhöhen.
16. Autounfall
Bei einem Unfall wird ein Autofahrer mit der Masse 75 kg durch einen Sicherheitsgurt auf einer Strecke von 0,4 m von 70 km/h auf 0 km/h abgebremst.
Berechne:
a) Die Verzögerung (negative Beschleunigung).
b) Wie groß ist die auf den Fahrer wirkende Kraft im Vergleich zur Gewichtskraft (F/G)?
Ausführliche Lösung
a)
Die Verzögerung beträgt etwa 472,608 m/s2.
b)
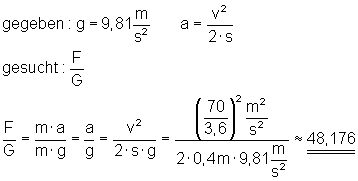
Das Verhältnis F/G beträgt etwa 48,176.
Das bedeutet, auf den Fahrer wirkt etwa das 48-fache seiner Gewichtskraft.
17. Fußball
Beim Fußballspielen erreicht ein straff geschossener Ball eine Geschwindigkeit von 90 km/h. Wenn der Torwart einen solchen Ball fangen will, muss er auf einer Strecke von etwa 25 cm die Geschwindigkeit des Balles auf 0 km/h herabsetzen.
Wie groß ist die durchschnittliche Kraft, die der Ball auf den Torwart ausübt?
(Masse des Balles: 500 g).
Ausführliche Lösung
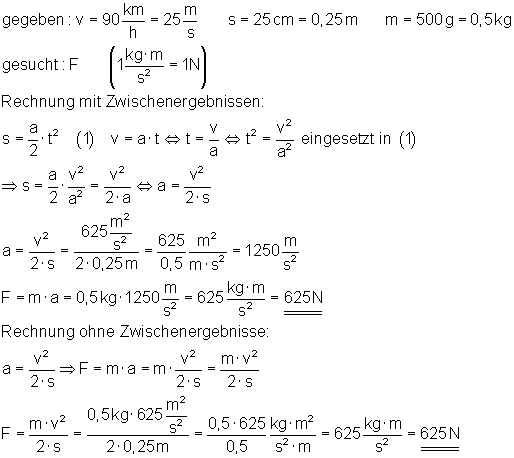
Der Ball übt eine Kraft von etwa 625 N auf den Torwart aus.
In den Fällen, in denen die Zwischenergebnisse gerundet werden, ist eine Gesamtrechnung ohne Zwischenergebnisse genauer, da dann keine Rundungsfehler auftreten.
18. Auto fährt gegen eine Wand
Bei einem Autounfall fährt ein PKW frontal mit einer Geschwindigkeit von 54 km/h gegen eine massive Wand. Durch die Knautschzone steht ein Bremsweg von 0,4 m zur Verfügung.
Mit dem wie vielfachen ihrer Gewichtskraft werden die Insassen nach vorne geschleudert?
Manche Kraftfahrer sind der Meinung, in der Stadt brauche man wegen der dort gefahrenen geringen Geschwindigkeiten keinen Sicherheitsgurt anzulegen. Nimm dazu Stellung!
Ausführliche Lösung

Auf die Insassen wirkt etwa das 29-fache ihrer Gewichtskraft.
Stellungnahme:
Auch niedrige Geschwindigkeiten können bei einem Auffahrunfall zu schweren Folgen führen. Die Verzögerung ist quadratisch von der Geschwindigkeit abhängig. Das Ergebnis obiger Rechnung zeigt, dass bei 54 km/h beim Aufprall auf die Insassen etwa das 29-fache ihrer Gewichtskraft wirkt. Das hat Knochenbrüche zur Folge, wenn nicht gar Schlimmeres.
19. Ein Jumbo-Jet startet
Die Masse eines beladenen Jumbo- Jets (Boeing 747) beträgt 340 t. Die 4 Triebwerke erzeugen zusammen eine Antriebskraft von 1000 kN. Wie lang muss die Startbahn des Flughafens sein, damit das Flugzeug die zum Abheben nötige Geschwindigkeit von 288 km/h erreichen kann?
Ausführliche Lösung
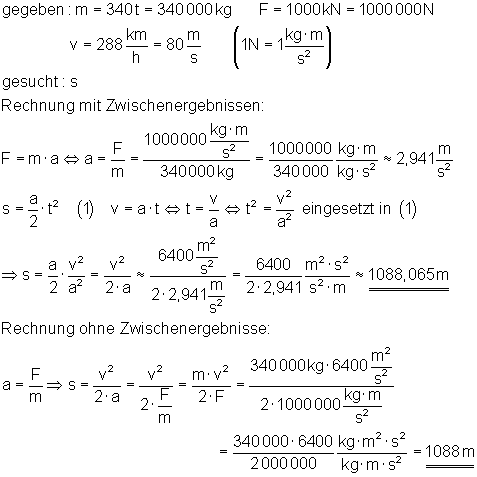
Die Startbahn muss mindestens 1088 m lang sein.
Die Rechnung ohne Zwischenergebnisse ist genauer, da sie keine Rundungsfehler enthält.
20. Verkehrsflugzeug startet
Ein unbeladenes Verkehrsflugzeug (40 t Masse) hebt nach dem Start mit einerGeschwindigkeit von 252 km/h ab. Die Startbahn ist 1,4 km lang.
a) Wie lange dauert es bis zum Abheben (a = konstant)?
b) Welche Beschleunigung und welche Kraft muss es beim Start erfahren?
c) Um wie viel muss die Startbahn verlängert werden, wenn die Zuladung 10 t beträgt und Abhebgeschwindigkeit so wie Beschleunigungskraft gleich bleiben sollen?
Ausführliche Lösung
a)
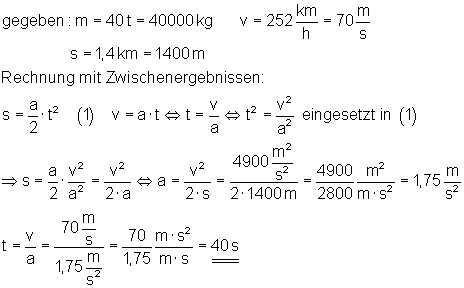
Die Zeit bis zum Abheben dauert 40 s.
b)
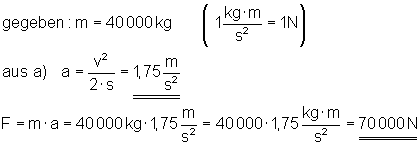
Die Beschleunigung beträgt 1,75 m/s2. Die Kraft 70 000 N.
c)

Die Startbahn muss um 350 m auf 1750 m verlängert werden.
Hier findest du die Aufgaben
und hier eine Übersicht über weitere Beiträge zum Thema Mechanik und Elektronik, darin auch Links zu Aufgaben.
Außerdem kannst du den Wikipediaartikel zur Beschleunigung lesen.