In meinem Beitrag Leistung, Energie und Energieumwandlung
habe ich das Thema für den Physikunterricht in Klasse 7 erklärt. Hier werde ich Leistung und Energie mit anderen Messwerten verknüpfen.
Im letzten Beitrag haben wir uns mit dem Messen und Berechnen von Energie beschäftigt. Wichtig ist jedoch auch die Frage wie schnell Energie übertragen wird. Damit kommen wir zur Definition von Leistung in der Physik. Durch Umstellen der Formel kommen wir zu der Aussage: Leistung mal Zeit ist übertragene Energie. Wenn wir die uns bereits bekannten Formeln für die Berechnung der physikalischen Arbeit und der Geschwindigkeit einsetzen, erhalten wir die Formel: Leistung ist Kraft mal Geschwindigkeit. Auch der Mensch verrichtet Arbeit, die wir in Watt messen können. Dazu gebe ich ein Rechenbeispiel, in dem die Leistung eines Lehrers und Schülers im Treppenhaus berechnet werden.
- Wie schnell wird Energie übertragen?
- Physikalische Definition Leistung, Beispiele, Einheit Leistung
- Leistung mal Zeit ist übertragene Energie, Rechenbeispiel
- Formel Leistung ist Kraft mal Geschwindigkeit
- Rechenbeispiel: Leistung von Lehrer und Schüler im Treppenhaus:
Wie schnell wird Energie übertragen?
Ein Sportauto und ein Oldtimer mit gleicher Masse (1500 kg ) fahren die gleiche Bergstrecke und beide gewinnen dabei 400 m Höhe.
Der Sportwagen brauchte dafür 100 s, der Oldtimer 400 s.
Oben angekommen sagt der Fahrer des Oldtimers:
„Unsere Autos haben beide die gleiche Höhenenergie bekommen. Die Motoren der Autos sind also gleich stark!“
Darf man so fragen?
Sicher nicht. Will man die beiden Motoren vergleichen, so fragt man besser nach der Energie, die sie jeweils in der gleichen Zeit liefern.
Aus diesem Grund führt uns dies auf den Begriff der Leistung.
Physikalische Definition Leistung
Leistung ist gleich Arbeit dividiert durch Zeit:
![]()
Die Einheit ist 1 J/s = 1 W (Watt) 1000 W = 1 kW
Dabei steht das P für die Leistung
W für Arbeit,
und t für die Zeit.
Rechenbeispiel:
Die Leistungen der beiden Autos aus obigem Beispiel:
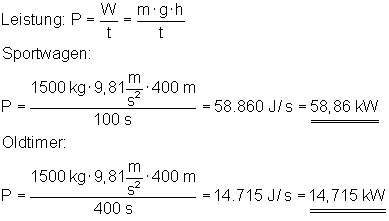
| Tabelle: Leistungen verschiedener Größenordnung | |
| Taschenrechner | 20 mW |
| Fahrraddynamo | 3 W |
| Haushaltsglühlampe | 25 – 100 W |
| Mensch ( dauernd ) | 80 W |
| kleiner Tauchsieder | 300 W |
| Heizung einer Wohnung | 20 kW |
| mittlerer Automotor | 50 kW |
| Diesellokomotive | 3 MW |
| ICE | 8 MW |
| Dampfturbine | 1000 MW |
Physikalische Einheit Leistung
Die Leistung von Automotoren wurde früher in Ps (Pferdestärke) statt in kW angegeben.
1 Ps war an der Leistung eines Pferdes orientiert.
![]()
Leistung mal Zeit ist übertragene Energie
Wenn wir die Formel für die Leistung
![]()
mit der Zeit t multiplizieren, dann stellt sich W, also die Energie als Leistung mal Zeit dar: ![]()
Energie wird deshalb in Wattsekunden Ws, Kilowattstunden kWh und in Joule J gemessen:
Es gilt dabei: 1 Ws = 1 J = 1 Nm 1 kWh = 3.600.000 Ws
Rechenbeispiel:
Ein Auto fährt mit konstanter Geschwindigkeit v = 108 km/h auf derAutobahn.
Untersuchungen im Windkanal ergaben, dass dabei der Luftwiderstand eine Kraft von 900 N auf das Auto ausübt.
Welche Motorleistung ist dazu erforderlich?
Dazu brauchen wir wieder die Formel für die Arbeit = Kraft mal Strecke, also W = F *s
und die Forml für die Geschwindigkeit = Strecke dividiert durch Zeit.
Wenn wir diese in die Formel einsetzen, ergibt sich:
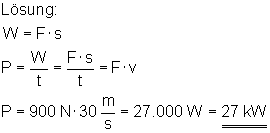
Formel Leistung ist Kraft mal Geschwindigkeit
Wird bei konstanter Kraft und konstanter Geschwindigkeit Energie übertragen, so gilt für die dazu erforderliche Leistung:
![]()
Dabei ist „P“ die Leistung
„F“ die Kraft
„v“ die Geschwindigkeit
Der Mensch in Watt gemessen
Ein Mensch selbst braucht pro Tag beim Nichtstun etwa 1 kWh = 3.6 MJ an Energie, bei Schwerstarbeit 4 kWh.
Die Intensität seines Energieumsatzes wird durch die Leistung P = W/t gekennzeichnet.
Beim Nichtstun sind das ca. 40 W, bei Schwerstarbeit 160 W.
Ein Mensch kann kurzzeitig maximal 1 kW Leistung erbringen.
Rechenbeispiel: Leistung von Lehrer und Schüler im Treppenhaus:
Ein Experiment zur Abschätzung. Ein Lehrer (75 kg) und ein Schüler (50 kg) rennen ein 7,5 m hohes Treppenhaus hoch.
Der Lehrer braucht 8,6 s, der Schüler 7,1 s.
Wer hat die größere Leistung erbracht?
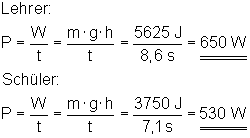
Obwohl der Schüler schneller läuft, leistet der Lehrer aufgrund seines Gewichts also mehr.
Hier findest du eine Übersicht über weitere Beiträge aus der Oberstufenphysik.