Hier findet ihr die Lösungen der Aufgaben zur Beschleunigung
1. Erkläre die Begriffe:
a) Eine gleichförmige Bewegung ist eine Bewegung, mit konstanter Geschwindigkeit.
b) Eine beschleunigte Bewegung ist eine Bewegung, bei der die Geschwindigkeit zunimmt.
c) Eine verzögerte Bewegung ist eine Bewegung, bei der die Geschwindigkeit abnimmt.
d) Beispiel zur gleichförmigen Bewegung: Ein ICE-Zug fährt auf freier Strecke in einem bestimmten Abschnitt mit gleichbleibender Geschwindigkeit, z. B. 240 km/h. Er legt dabei in gleichen Zeitabschnitten gleiche Wege zurück.
Beispiel zur beschleunigten Bewegung: Ein Auto fährt an der Ampel an. Dabei wird es immer schneller, seine Geschwindigkeit nimmt zu. In gleichen Zeitabschnitten legt das Auto immer größere Wege zurück.
Beispiel zur verzögerten Bewegung: Ein Auto, das abbremst, verliert Geschwindigkeit, es wird immer langsamer. In gleichen Zeitabschnitten werden kürzere Wege zurückgelegt.
2. Ein Sportwagen startet mit einer konstanten Beschleunigung :
Hier habe ich erklärt, wie man die Geschwindigkeit berechnet.
Und hier habe ich erklärt, wie man wie man von \frac{km}{h} in \frac{m}{s} umrechnet und umgekehrt.
In diesem 📽 Video erkläre ich außerdem, wie man \frac{m}{s} in \frac{km}{h} umrechnet.
a) Welche Geschwindigkeit erreicht er
Eine ähnliche Aufgabe mit anderen Werten erkläre ich in diesem 📽 Video Geschwindigkeit berechnen mit Beschleunigung und Zeit.
gegeben: a = 4\dfrac{m}{s^2} t = 8s \\
gesucht: v in m/s und km/h
v = a· t = 4\dfrac{m}{s^2} · 8s = 4 · 8 \dfrac{m · s}{s · s} = 32\dfrac{m · \cancel s}{s · \cancel s} = \underline{\underline{32\dfrac{m}{s}}} \\1 \dfrac{m}{s} = 3,6 \dfrac{km}{h} \Rightarrow 32\dfrac{m}{s} = 32 · 3,6 \dfrac{km}{h} = \underline{\underline{115,2\dfrac{km}{h}}}
Nach 8 s erreicht der Sportwagen eine Geschwindigkeit von v = 32 m/s = 115,2 km/h.
b) Wie groß ist der in 8 s zurückgelegte Weg?
Hier habe ich erklärt, wie man die Strecke berechnet.
Eine Aufgabe mit anderen Werten erkläre ich in diesem 📽 Video Strecke berechnen mit Beschleunigung und Zeit.
gegeben: a = 4\dfrac{m}{s^2} ; t = 8s ; gesucht: s
s = \dfrac{a · t^2}{2} = \dfrac{4\dfrac{m}{s^2} · (8s)^2}{2} = \dfrac{4\dfrac{m}{s^2} · 64 s^2}{2} = \dfrac{4 · 64 \dfrac{m · s^2}{s^2}}{2} = \dfrac{4 · 64 \dfrac{m · \cancel s^2}{\cancel s^2}}{2} = \dfrac{256m}{2} = \underline{\underline{128 m}}Der in 8 s zurückgelegte Weg beträgt 128 m.
3. Ein Kampfjet fliegt mit einer Geschwindigkeit von 720 km/h.:
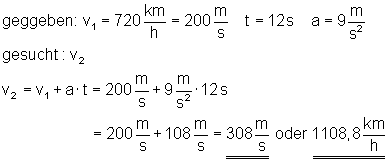
Nach der Beschleunigungsphase hat das Kampfflugzeug eine Geschwindigkeit von v = 308 m/s oder 1108,8 km/h.
4. Zeichne ein v t Diagramm:
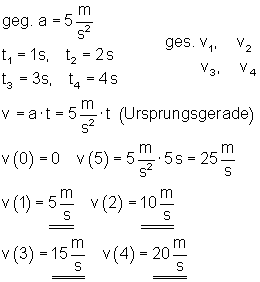
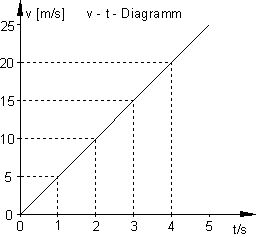
5. Mit zwei Motorrädern wird ein Beschleunigungstest gemacht.:
Hier habe ich ein ähnliches Beispiel für Motorrad 1 gerechnet.
Und hier für Motorrad 2.
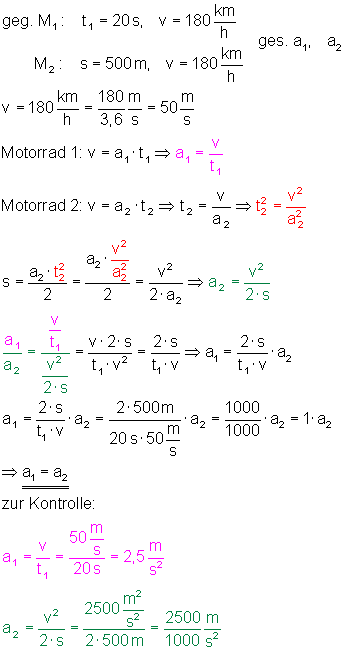
Die beiden Motorräder haben die gleichen Beschleunigungswerte, denn a1 = a2 = 2,5 m/s2
6. Ein Raketenwagen erreicht bei konstanter Beschleunigung :
Eine ähnliche Aufgabe mit anderen Werten habe ich in diesem 📽️ Video Zeit und Beschleunigung berechnet erklärt.
Außerdem findet ihr hier alle Formeln zur Beschleunigung.
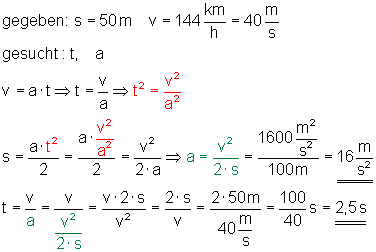
Der Raketenwagen braucht t = 2,5 s. Die Beschleunigung beträgt a = 16 m/s2.
7. Wie groß ist der in dieser Zeit zurückgelegte Weg?:
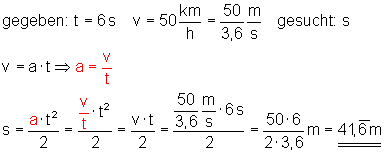
Der in 6 Sekunden zurückgelegte Weg beträgt s = 41 2/3 m.
8. Wie groß ist die Beschleunigung?:
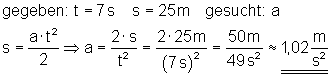
Die Beschleunigung beträgt etwa 1,02 m/s2.
9. Wie weit ist er gefahren?:
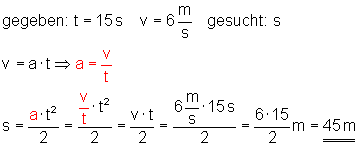
Der Castor Transport ist in 15 Sekunden 45 m weit gefahren.
10. Wie groß sind Beschleunigung und Geschwindigkeit?:
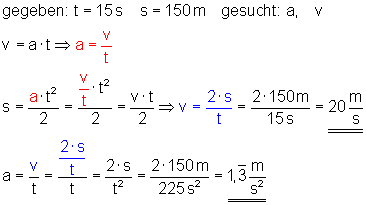
Die Beschleunigung beträgt 1 1/3 m/s2. Die Geschwindigkeit nach 15 s beträgt etwa 20 m/s.
11. Mit welchen Werten muss die Maschine beschleunigen?
Endgeschwindigkeit des Flugzeugs: v = 75 m/s = 270 km/h.
Gesamte Beschleunigungsstrecke: s = 1200 m.
Gesucht ist der nötige Beschleunigungswert.
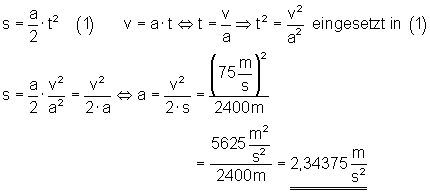
Die Passagiermaschine muss mindestens mit etwa 2,35 m/s2 beschleunigen.
12. Ein Pfeil wird beschleunigt
a) Die Beschleunigung ist nicht konstant, da sich die Kraft, die die Sehne auf den Pfeil ausübt, ändert.
b)
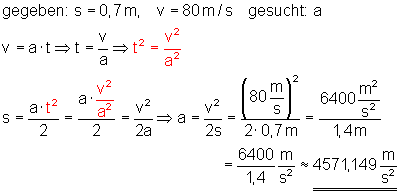
Die mittlere Beschleunigung beträgt etwa 4571,149 m/s2.
c)
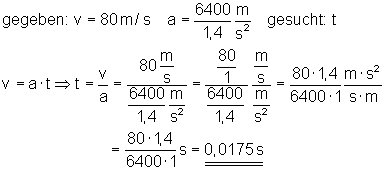
Der Beschleunigungsvorgang dauert t = 0,0175 s.
Hier findest du die Aufgaben.
Hier die Theorie zur Beschleunigung.
Und hier geht es um Beschleunigung aus der Bewegung und Bremsweg.
Und hier eine Übersicht über weitere Beiträge zum Thema Mechanik und Elektronik, darin auch Links zu Aufgabe.