Beschleunigung mit Anfangsgeschwindigkeit und Bremsweg
Physik Klasse 10
In diesem Beitrag wiederhole ich anhand von Beispielen Bewegungen mit gleichbleibender Geschwindigkeit und gleichmäßig beschleunigte Bewegung. Danach erkläre ich die Formeln mit Anfangsgeschwindigkeit. Anschließend beschäftige ich mich mit dem Bremsweg, Reibung und Verzögerung. Schließlich geht es um den Anhalteweg, der sich aus Reaktionsweg plus Bremsweg berechnet.
- Bewegung mit konstanter Geschwindigkeit
- Gleichmäßig beschleunigte Bewegung
- Beschleunigung mit vorgegebener Anfangsgeschwindigkeit
- Verzögerung mit vorgegebener Anfangsgeschwindigkeit
- Bremsweg Formel berechnen
- Reibung und Verzögerung
- Anhalteweg aus Reaktionsweg und Bremsweg berechnen
1. Bewegung mit konstanter Geschwindigkeit
Wir haben uns bereits mit Bewegungen mit gleichbleibender Geschwindigkeit beschäftigt und dafür das Weg-Zeit-Diagramm und Geschwindigkeit-Zeit-Diagramm gezeichnet.
Dabei arbeiten wir mit folgenden Variablen:
s : steht für die Strecke in m Metern. s/m bedeutet also Strecke in Metern
t : steht für die Zeit in s Sekunden. t/s bedeutet also Zeit in Sekunden.
Daraus errechnen wir:
v : die Geschwindigkeit, also s/t : Strecke dividiert durch Zeit.
Die Basiseinheit zur Messung der Geschwindigkeit ist Meter pro Sekunde \frac{m}{s} .
Im alltäglichen Sprachgebrauch wird aber oft die Einheit Kilometer pro Stunde \frac{km}{h} in \frac{m}{s}verwendet.
Geschwindigkeits-Zeit und Weg-Zeit Diagramme
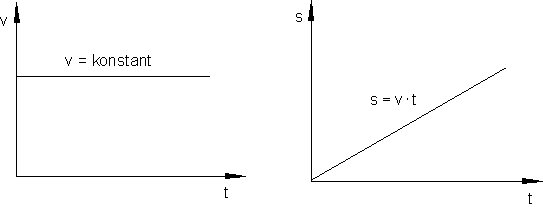
Wir sehen daran, der Gegenstand bewegt sich mit konstanter Geschwindigkeit v. Außerdem nimmt die zurückgelegte Strecke s mit der Zeit zu.
Hier noch einmal die Formel:
\color{red}{\large{s = v \cdot t}}
Hier noch einmal ein Beispiel dazu:
Ein Auto fährt 12 Sekunden lang mit der Geschwindigkeit 10 \frac{m}{s}. Welche Strecke legt es dabei zurück?
gegeben: v = 10 m/s, t = 12 s, gesucht: s.
s = v \cdot t = 10 \frac{m}{s} \cdot 12s
= 10 \cdot 12 \frac{m}{s} \cdot s = \underline{\underline{120 m}}
Hier habe ich die gleichmäßige Bewegung ausführlich erklärt. Außerdem gibt es hier Aufgaben dazu: Aufgaben zur gleichförmigen Bewegung.
2. Gleichmäßig beschleunigte Bewegung
Danach hatten wir uns mit der gleichmäßig beschleunigten Bewegung beschäftigt.
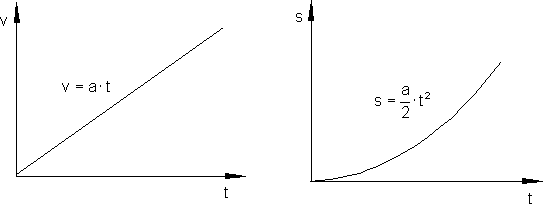
Diesmal sehen wir eine gleichmäßig größer werdende Geschwindigkeit v. Außerdem nimmt die zurückgelegte Strecke s immer mehr zu.
Hier noch einmal die Formel:
\color{red}{\large{v = a \cdot t}}
Auch hierzu wieder ein Beispiel:
Ein Auto beschleunigt aus dem Stillstand 6 Sekunden lang mit der Beschleunigung a = 3 \frac{m}{s^2} . Welche Geschwindigkeit hat es danach? Und welchen Weg hat es dadurch zurückgelegt?
gegeben: a = 3 \frac{m}{s^2} , t = 6s.
gesucht: Geschwindigkeit v, Weg s.
v = a \cdot t = 3 \frac{m}{s^2} \cdot 6s
= 3 \cdot 6s \frac{m}{s^2} \cdot s = \underline{\underline{18 \frac{m}{s} }}
s = \frac{1}{2} \cdot a \cdot t^2 = \frac{1}{2} \cdot 3 \frac{m}{s^2} \cdot 36s^2
= \frac{1}{2} \cdot 3 \cdot 36 \frac{m}{s^2} \cdot s^2 = \underline{\underline{54 m}} .
Im Beitrag Die gleichmäßig beschleunigte Bewegung habe ich dies ausführlich erklärt. Hier gibt es Aufgaben dazu: Aufgaben zur beschleunigten Bewegung.
3. Beschleunigung mit vorgegebener Anfangsgeschwindigkeit
Wir haben bis jetzt hauptsächlich Körper betrachet, die sich aus einer Ruheposition aus in Bewegung setzt. Nun schauen wir uns Gegenstände an, die zusätzlich beschleunigen.
Beispiel
Ein Auto fährt 10 Sekunden lang mit der konstanten Geschwindigkeit v0 = 20 m/s.
Danach wird es t = 5 Sekunden lang mit a = 1 m/s2 beschleunigt.
Wie groß ist dann die Endgeschwindigkeit ve?
Welchen Weg s legt das Auto bei diesem Vorgang zurück?
Zeichne das v/t und das s/t- Diagramm für diesen Vorgang.
Gegeben:
| t0 = 10 s | Zeit für konstante Geschwindigkeit v0 |
|---|---|
| t1 = 5 s | Beschleunigungszeit |
| v0 = 20 s\frac{m}{s} | Anfangsgeschwindigkeit |
| a = 1 \frac{m}{s^2} | Beschleunigung |
Für die Endgeschwindigkeit nach dem Beschleunigungsvorgang gilt:
v _e = v _0 + a \cdot t_1 = 20\frac{m}{s} + 1\frac{m}{s^2} \cdot 5s
= 20\frac{m}{s} + 5\frac{m}{s} = \underline{\underline{25\frac{m}{s}}}
Der bei diesem Vorgang zurückgelegte Weg beträgt:
s = v_0 \cdot t_0 + \cdot v_0 \cdot t_1 + \frac{1}{2} \cdot a \cdot t_1^2
= 20 \frac{m}{s} \cdot 10s + 20 \frac{m}{s} \cdot 5s + \frac{1}{2} \cdot 1\frac{m}{s^2} \cdot 25s^2
= 200m + 100m + 12,5m = \underline{\underline{312,5 m}}
Schauen wir uns dies mal in den Diagrammen an:
Geschwindigkeits-Zeit-Diagramm Weg-Zeit-Diagramm
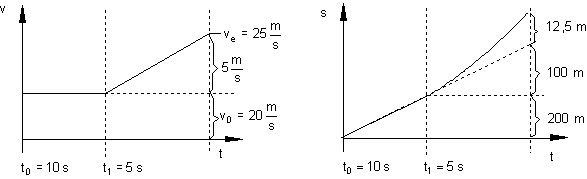
Daraus schließen wir: Wird ein Körper, der sich während der Zeit t0 mit der Geschwindigkeit v0 bewegt, während der Zeit t1 beschleunigt, so gelten folgende Formeln:
Formel zur Berechnung der Geschwindigkeit bei Beschleunigung:
💡
| \color{red}{\large{v_e = v_0 + a \cdot t_1}} |
Formel zur Berechnung der Strecke bei Beschleunigung:
💡
| \color{red}{\large{s = v_0 \cdot t_0 + v_0 \cdot t_1 + \frac{1}{2} \frac{m}{s} \cdot a \cdot \frac{m}{s} t_1^2}} |
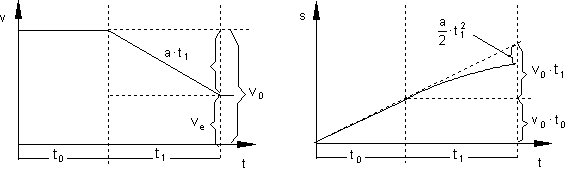
In den Diagrammen sieht das folgendermaßen aus:
Geschwindigkeits-Zeit-Diagramm Weg-Zeit-Diagramm
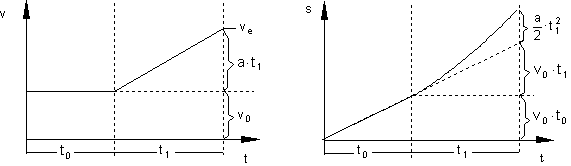
4. Verzögerung mit vorgegebener Anfangsgeschwindigkeit
Nun betrachten wir den umgekehrten Fall: Ein bereits fahrendes Auto bremst.
Zur Erinnerung: Bei
- einer beschleunigten Bewegung nimmt die Geschwindigkeit zu.
- einer verzögerten Bewegung nimmt die Geschwindigkeit ab.
- der gleichmäßig verzögerten Bewegung wirkt eine konstante Beschleunigung der Bewegung entgegen, der Körper wird langsamer. Mit anderen Worten: er wird abgebremst.
Aufgabe
Ein Auto fährt 10 Sekunden lang mit der konstanten Geschwindigkeit v0 = 20 s\frac{m}{s}.
Danach wird es t = 5 s lang mit a = 1 \frac{m}{s^2} verzögert.
Wie groß ist dann die Endgeschwindigkeit ve?
Welchen Weg s legt das Auto bei diesem Vorgang zurück?
Zeichne das v/t und das s/t- Diagramm für diesen Vorgang!
Gegeben:
| t0 = 10 s | Zeit für konstante Geschwindigkeit v0 |
|---|---|
| t1 = 5 s | Verzögerungsszeit |
| v0 = 20 s\frac{m}{s} | Anfangsgeschwindigkeit |
| a = 1 \frac{m}{s^2} | Verzögerung |
Für die Endgeschwindigkeit nach dem Verzögerungsvorgang gilt:
v _e = v _0 - a \cdot t_1 = 20\frac{m}{s} - 1\frac{m}{s} \cdot 5s
= 20\frac{m}{s} - 5\frac{m}{s} = \underline{\underline{15\frac{m}{s}}}
Der bei diesem Vorgang zurückgelegte Weg beträgt:
s = v_0 \cdot t_0 + \cdot v_0 \cdot t_1 - \frac{1}{2} \cdot a \cdot t_1^2
= 20 \frac{m}{s} \cdot 10s + 20 \frac{m}{s} \cdot 5s - \frac{1}{2} \cdot 1\frac{m}{s^2} \cdot 25s^2
= 200m + 100m - 12,5m = \underline{\underline{287,5 m}}
Geschwindigkeits-Zeit-Diagramm Weg-Zeit-Diagramm
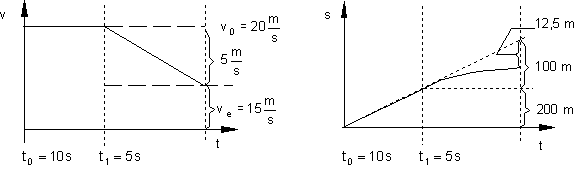
Daraus schließen wir: Wird ein Körper, der sich während der Zeit t0 mit der Geschwindigkeit v0 bewegt, während der Zeit t1 abgebremst (verzögert), so gelten folgende Formeln:
Formel zur Berechnung der Geschwindigkeit bei Verzögerung:
💡
| \color{red}{\large{v_e = v_0 - a \cdot t_1}} |
Formel zur Berechnung der Strecke bei Verzögerung:
💡
| \color{red}{\large{s = v_0 \cdot t_0 + v_0 \cdot t_1 - \frac{1}{2} \frac{m}{s} \cdot a \cdot \frac{m}{s} t_1^2}} |
5. Bremsweg Formel berechnen
Fassen wir noch einmal zusammen: Wird ein Körper mit vorgegebener Anfangsgeschwindigkeit verzögert, dann gelten diese beiden Formeln:
v_e = v_0 - a \cdot t
s = v_0 \cdot t_0 + v_0 \cdot t_1 - \frac{1}{2} \cdot a \cdot t_1^2
Soll ein Körper bis zum Stillstand abgebremst werden, so ist die Endgeschwindigkeit v_e = 0
Wenn wir dies in die Formel v _e = v _0 - a \cdot t_1 = einsetzen, gilt: 0 = v_0 - a \cdot t_1.
Danach stellen wir dies nach v0 um und erhalten: v_0 = a \cdot t_1
Dabei ist t1 die Bremszeit.
Wenn wir dies nach t1 umstellen ergibt sich: t_1 = \frac{v_0}{a} .
Das Weg-Zeit-Gesetz für die gleichmäßig beschleunigte (oder verzögerte) Bewegung lautet:
s = \frac{a}{2} \cdot t^2.
Setzt man in diese Formel für die Zeit t den Ausdruck für t1, dann erhalten wir für die Strecke:
s = \frac{a}{2} \cdot t^2 = \frac{a}{2} \cdot t \cdot t = \frac{a}{2} \cdot \frac{v_0}{a} \cdot \frac{v_0}{a} = \frac{v_0^2}{2a}
Die Formel für den Bremsweg lautet also:
💡
| \color{red}{\large{s = \frac{v_0^2}{2a}}} |
Der Bremsweg hängt also nur von dem Quadrat der Anfangsgeschwindigkeit (v0 )2 und der Verzögerung a ab.
Wie groß aber ist dabei die Verzögerung? Wovon hängt sie ab, wenn ein Auto bremst?
6. Reibung und Verzögerung
Versuch
Wir untersuchen die Reibung eines Klotzes, (Haftreibung und Gleitreibung).
Für die Reibungskraft gilt: F_r = \mu \cdot m \cdot g
Dabei steht \mu für die Reibungszahl. Diese beträgt auf trockenem Asphalt \mu = 0,7 .
r steht für den Durchmesser des Gegenstands, hierbei der Reifen.
g steht für die Erdbeschleunigung (9,81 \cdot \frac {m}{s^2}) .
Das Newtonsche Kraftgesetzt lautet: F = m \cdot a.
Es gilt auch für die Reibungskraft Fr.
Wenn man diese beiden Formeln F_r = m \cdot a und F_r = \mu \cdot m \cdot g zusammen bringt, folgt:
m \cdot a = \mu \cdot m \cdot g => \underline{\underline{a = \mu \cdot g}}
Die Verzögerung ist also nur von der Reibungszahl und der Erdbeschleunigung abhängig.
7. Anhalteweg aus Reaktionsweg und Bremsweg berechnen
Viel wichtiger als die Bremszeit ist der Anhalteweg. Wenn ein Autofahrer zum Beispiel plötzlich eine Gefahr sieht, muss er eine Vollbremsung machen. Dies geschieht in folgenden Phasen:
Schrecksekunde (je nach Zustand des Fahrers ) ts = 1 Sekunde.
Ansprechzeit der Bremse (von der Auslösung bis zur Wirkung) ta = 0,3 Sekunde.
Bremszeit bis zum Stillstand des Autos ( tb = v0 / a) (t_b = \frac {v_0}{a})
Für die Anhaltezeit gilt: Schrecksekunde + Ansprechzeit + Bremszeit.
Für den Anhalteweg gilt: Reaktionsweg + Bremsweg.
Beispiel
Ein Auto fährt mit der konstanten Geschwindigkeit v = 90 km/h. Wie groß ist die Anhaltezeit und der Anhalteweg auf trockener Straße?
Anhaltezeit = Schrecksekunde + Ansprechzeit + Bremszeit:
t_a = 1s + 0,3 s + \frac {v_0}{\mu \cdot g}
= 1s + 0,3 s + \frac {25 \frac{m}{s}} {0,7 \cdot 9,81\frac{m}{s^2}}
= 1,3s + 3,63s = \underline{\underline{4,49s}}
Anhalteweg = Reaktionsweg + Bremsweg.
s_a = v_0 \cdot (t_s + t_a) + \frac {v_0^2}{2 \cdot \mu \cdot g}= 25 \frac {m}{s} \cdot 1,3s + \frac {625 \frac {m^2}{s^2}} {2 \cdot 0,7 \cdot 9,81 \frac {m}{s^2}}
= 32,5m + 45,5m = \underline{\underline{78 m}}
In der Fahrschule verwendet man eine Faustformel für den Anhalteweg.
Es gilt: Anhalteweg = (Tachoanzeige / 10 )2 + 3 mal Tachoanzeige / 10 (in Meter)
Für obiges Beispiel wäre das:
Anhalteweg = ( 90 /10 )2 +3 mal (90/10)= 9 mal 9 + 3 mal 9 = 81 + 27 = 108 m.
Wir sehen, die Faustformel gilt recht gut. Sie gilt aber nur bei trockener Straße, guten Reifen und Bremsen und bei einem normalen Verhalten des Fahrers. Deshalb immer mindestens Tachoabstand zum vorderen Fahrzeug halten.
Hier finden Sie die Aufgaben zum Thema.
Hier geht es um Die gleichmäßig beschleunigte Bewegung.
Und hier eine Übersicht über weitere Beiträge zum Thema Mechanik und Elektronik, darin auch Links zu weiteren Aufgaben.
