Ich stelle Aufgaben zur Flächenberechnung bei Quadrat, Rechteck, Dreieck, Trapez, Kreis, Kreisring und Kreisausschnitt zur Verfügung. Dabei stelle ich zuerst die Formel vor. Dann zeige ich anhand eines Beispiels, wie die Fläche berechnet wird und verdeutliche dies mit einer Zeichnung. Danach können Sie eine Aufgabe lösen. Die ausführlichen Lösungen finden Sie in einem weiteren Beitrag.
1. Aufgaben Flächenberechnung Quadrat
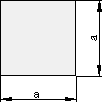
Die Fläche wird folgendermaßen berechnet: \color{red}{\large{A = a \cdot a = a^2}}
Beispiel:
Berechne die Fläche eines Quadrats
mit der Seitenlänge a = 12 cm!
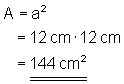
Berechne dies jetzt mit a = 3,75 dm!
2. Rechteck
Die Fläche wird so berechnet: \color{red}{\large{A = a \cdot b}}
Beispiel:
Berechne die Fläche eines Rechtecks mit den Seitenlängen
a = 12 cm und b = 20 cm!
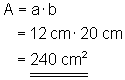
Berechne mit a = 3,75 dm, b = 22 cm
3. Dreieck
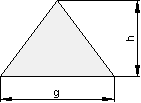
Die Fläche wird folgendermaßen berechnet: Grundseite mal Höhe durch 2:
\color{red}{\large{A = \frac{g \cdot h}{2}}}
Beispiel:
Berechne die Fläche eines Dreiecks mit den Längeng = 14 cm und h = 10 cm!
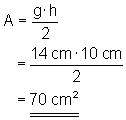
Berechne mit g = 3,75 dm, h = 21 cm
4. Trapez
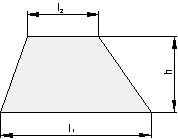
Die Fläche wird so berechnet: \color{red}{\large{A = \frac{I_1 + I_2}{2} \cdot h}}
Beispiel:
Berechne die Trapezfläche
l1 = 12 m, l2 = 6 m, h = 8 m!
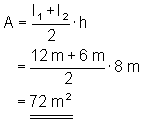
Berechne mit
l1 = 4,75 dm, l2 = 36 cm, h = 220 mm!
5. Kreis
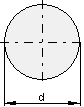
Die Fläche wird so berechnet: \color{red}{\large{A = \frac{d^2 \cdot \pi}{4} = r^2 \cdot \pi}}
\pi wird auch Kreiszahl genannt und hat ungefähr den Wert 3,1415629.
Beispiel:
Berechne die Fläche eines Kreises mit dem Durchmesser d = 120 mm!
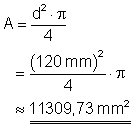
Berechne mit d = 12,7 m!
6. Kreisring
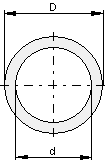
Die Fläche wird so berechnet: \color{red}{\large{A = (D^2 - d^2) \cdot \frac{\pi}{4} = r^2 \cdot \pi}}
Beispiel:
Berechne die Fläche eines Kreisringes mit dem Innendurchmesser d = 60 mm und dem Außendurchmesser D = 80 mm!
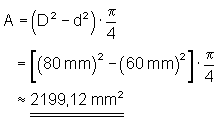
Berechne mit D = 12,7 dm, d = 95 cm
7. Kreisausschnitt
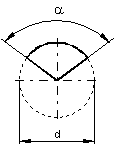
Die Fläche wird so berechnet: \color{red}{\large{A = \dfrac{d^2 \cdot \pi \cdot \alpha}{4 \cdot 360°}}}
Beispiel:
Berechne die Fläche eines Kreisausschnitts mit d = 120 mm!
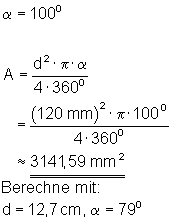
Hier findest du die Lösungen hierzu.
Hier findest du eine Tabellen zum Umrechnen von Zehnerpotenzen, Längen, Flächen, Volumen mit Übungsaufgaben und Lösungen.
Und hier eine Übersicht über alle Beiträge zum Thema Geometrie, darin auch Links zu weiteren Aufgaben.


