In diesem Beitrag werde ich als erstes erklären, was Dezimalbrüche sind. Dann Beispiele vorstellen und erklären, wie man einen Bruch in einen Dezimalbruch verwandelt und umgekehrt.
- Definition Dezimalbruch
- Beispiele endlicher Dezimalbruch und unendlicher Dezimalbruch
- Dezimalbruch in einen Bruch umwandeln und umkehrt
Definition Dezimalbruch
Zahlen mit einem Komma und Ziffern dahinter nennt man Dezimalzahlen.
Hier ein Beispiel:
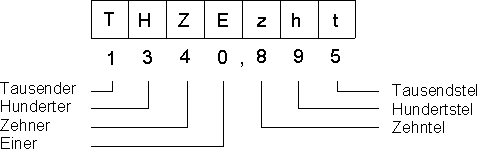
Diese Zahl kann man auch durch einen Bruch, in diesem Fall eine Division durch Eintausend darstellen,
deshalb spricht man auch von einem Dezimalbruch.
Das Wort Dezimal kommt aus dem Lateinischen und bedeutet 10,
alle diese Brüche haben im Nenner nämlich Zahlen, die Vielfache von 10 sind.
Ein Dezimalbruch (Dezimalzahl) entsteht, wenn man einen Bruch ausdividiert,
also Zähler (das was über dem Bruchstrich steht) dividiert durch den Nenner (das, was unter dem Bruchstrich steh).
Geht die Division auf, dann heißt er endlicher Dezimalbruch.
Beispiel endlicher Dezimalbruch:
Wenn die Division nicht möglich ist, zum Beispiel bei der Division durch 3, dann wiederholen sich die Ziffern in einer bestimmten regelmäßigen Folge. So eine Zahl nennt man einen unendlich periodischen Dezimalbruch. Damit man das erkennt, macht man einen Strich über den Nachkommastellen.
Beispiel unendlich periodischer Dezimalbruch:
Wie wandelt man einen Dezimalbruch in einen Bruch um?
Man kann jede Zahl mit Nachkommastellen in einen Dezimalbruch umwandeln. Umgekehrt kann man ebenso jeden Dezimalbruch als Zahl mit Nachkommastellen darstellen.
Umwandlung unendlicher periodischer Dezimalbrüche in Brüche
Hierbei rechnet man rückwärts:
Man multipliziert den unendlich periodischen Dezimalbruch mit Zehn. Dann schaut man, mit welcher Zahl man den Rest multiplizieren muss, damit man die Ziffern mit dem Strich darüber subtrahieren kann:
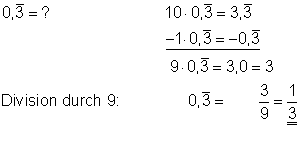
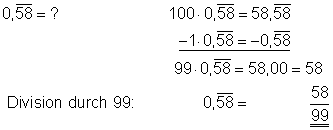
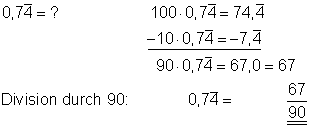
Hier findest du Aufgaben dazu und die Lösungen der Aufgaben.
Außerdem Aufgaben dazu I und Lösungen der Aufgaben I.
Und Aufgaben II und die Lösungen II.
Hier findest du eine Übersicht über alle Beiträge zur Bruchrechnung.
Und hier eine Übersicht über alle Beiträge zu den mathematischen Grundlagen, darin auch Links zu weiteren Aufgaben und Videos.
