Hier kannst du Aufgaben mit Brüchen üben, bist du Bruchrechnen kannst. Dabei sollst du Brüche addieren, subtrahieren, multiplizieren, dividieren, aus gemischten Zahlen Brüche machen.
1. Addiere folgende Brüche. Falls nötig, mache die Brüche vorher gleichnamig.
Mit anderen Worten: Dazu muss man die Brüche erweitern. Wie man Brüche erweitert und kürzt kannst du dir auch in diesem 
Video Bruch erweitern und kürzen ansehen.
Und dazu muss man das kleinste gemeinsame Vielfache der Nennen finden. Das kannst du dir in diesem shorts Kleinstes gemeinsames Vielfaches anschauen.
a) dfrac{1}{2} + dfrac{2}{3}
Diese Aufgabe erkläre ich auch in diesem shorts Brüche addieren.
b) dfrac{1}{3} + dfrac{1}{5}
c} dfrac{1}{2} + dfrac{1}{4} + dfrac{1}{8}
d} dfrac{7}{8} + dfrac{2}{7} + dfrac{1}{4}
2. Subtrahiere folgende Brüche. Falls nötig, mache sie vorher gleichnamig!
a) dfrac{3}{2} - dfrac{1}{3}
b) dfrac{5}{7} - dfrac{1}{2}
c) dfrac{9}{2} - dfrac{1}{3} - dfrac{1}{4}
d) dfrac{7}{8} - dfrac{2}{5} - dfrac{1}{10}
3. Multipliziere folgende Brüche. Falls möglich, kürze das Ergebnis.
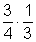
Diese Aufgabe erkläre ich auch in diesem shorts Brüche multiplizieren und dividieren.
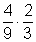
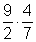
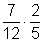
4. Dividiere folgende Brüche. Falls möglich, kürze das Ergebnis!
Wie man Brüche dividiert erkläre ich auch in diesem shorts Brüche dividieren.
a) dfrac{4}{3} : dfrac{2}{5}
b) dfrac{3}{8} : dfrac{2}{3}
c) dfrac{7}{5} : dfrac{4}{3}
d) dfrac{12}{7} : dfrac{7}{5}
5. Mache zuerst aus den gemischten Zahlen Brüche, dann löse die Aufgabe
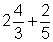
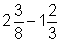
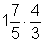
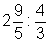
Hier findest du die Lösungen.
Hier die Theorie hierzu: Einführung in die Bruchrechnung.
Und hier Dezimalbrüche.
weitere Aufgaben:
Bruchrechnen Aufgaben I Lösungen der Aufgaben I.
Hier findest du eine Übersicht über alle Beiträge zu den mathematischen Grundlagen, darin auch Links zu weiteren Aufgaben.
