Bruchrechnen einfach erklärt

Bruchrechnen, Mathematik, Sekundarstufe 1

In diesem Beitrag erkläre ich das Bruchrechnen leicht verständlich und mit vielen anschaulichen Beispielen. Vor allem erkläre ich die wichtigsten Bruchregeln: Brüche kürzen, erweitern, gleichnamig machen, addiere, subtrahieren, multiplizieren und dividieren.

  1. Leckere Beispiele
  2. Definition Bruch in der Mathematik
  3. Negative Bruchzahl und gemischte Zahlen auf der Zahlengeraden
  4. Regeln zur Bruchrechnung:
  5. kürzen
  6. erweitern
  7. gleichnamig machen
  8. addieren
  9. subtrahieren
  10. multiplizieren
  11. dividieren

1. Schokoladenbeispiele

1 Tafel Schokolade soll gleichmäßig an 4 Personen verteilt werden. Dann erhält jede Person ein Viertel der Tafel. Das schreiben wir so:

Wir schreiben 1 : 4 = \dfrac{1}{4} 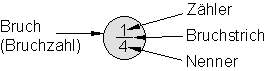Brüche-Darstellung

Was über dem Bruchstrich steht, nennt man Zähler, was darunter steht, Nenner.

Aufteilungsbeispiele

Wenn wir mehr Schokolade haben und drei Tafeln an vier Personen verteilen, bekommt jeder 3 mal ein Viertel einer Tafel. (Wir müssen dann allerdings aufpassen, dass wir nicht alles auf einmal essen, sonst bekommen wir Bauchschmerzen!) Das kann man so schreiben:

Anz. der TafelnAnz. d. PersonenBruch
3   4 3 : 4 = \frac{3}{4}
7 9 7 : 9 = \frac{7}{9}

Definition Bruch in der Mathematik

Ein Bruch ist eine Zahl mit der Form: \dfrac{Zähler}{Nenner}

Zähler und Nenner sind ganze Zahlen ( \in \mathbb{Z} );

Nenner \neq 0 .

Der Bruchstrich ist gleichbedeutend mit einem Divisionszeichen.

Negative Bruchzahl

Beispiel    

 (-1) : 4 = \dfrac{-1}{4} = - \dfrac{1}{4}

Bruchzahlen lassen sich auch auf der Zahlengeraden darstellen.

des_048

Gemischte Zahl

Sie bestehen aus ganzen Zahlen und Brüchen.

Beispiel:

 \dfrac{5}{3} = 5 : 3 = 1 \, Rest \, 2 \qquad 

also \, \dfrac{5}{3} = 1\dfrac{2}{3} 

umgekehrt:   1\dfrac{2}{3} = \dfrac{1 \cdot 3 +2}{3} = \dfrac{5}{3}

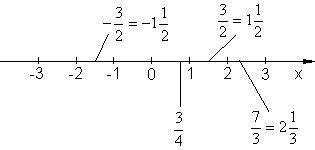
Die wichtigsten Regeln beim Bruchrechnen

Brüche kürzen und erweitern

Man kürzt Brüche, indem man Zähler und Nenner durch die selbe Zahl dividiert.

 \dfrac{2}{6} = \dfrac{2 : 2}{6 : 2} = \underline{\underline{\dfrac{1}{3}}}
\dfrac{9}{3} = \dfrac{9 : 3}{3 : 3} = \dfrac{3}{1} = \underline{\underline{3}}

Wie man Brüche erweitert und kürzt kannst du dir auch in diesem 📽 Video Brüche erweitern und kürzen ansehen.

Wenn man Brüche erweitert, dann multipliziert man Zähler und Nenner mit derselben Zahl.
 \dfrac{2}{5} = \dfrac{2 \cdot 2}{5 \cdot 2} = \underline{\underline{\dfrac{4}{10}}} 

\dfrac{3}{7} = \dfrac{3 \cdot 3}{7 \cdot 3} = \underline{\underline{\dfrac{9}{21}}}

Man kann jede ganze Zahl als Bruch mit dem Nenner 1 darstellen. Das ist besonders hilfreich bei der Division von Brüchen und Zahlen.

 \dfrac{3}{4} : 2 = \dfrac{3}{4} : \dfrac{2}{1} = \dfrac{3 \cdot 1}{4 \cdot 2} = \underline{\underline{\dfrac{3}{8}}}

 3 : \dfrac{2}{5} = \dfrac{3}{1} : {2}{5} = \dfrac{3 \cdot 5}{1 \cdot 2} = \underline{\underline{\dfrac{15}{2}}}

Brüche gleichnamig machen

Bevor man ungleichnamige Brüche addieren oder subtrahieren kann, muss man sie erst gleichnamig machen. Mit anderen Worten: im Nennen, also unter dem Bruchstrich, muss die gleiche Zahl stehen. Dazu suchen wir das kleinste gemeinsame Vielfache (kgV) der Nennen. (Wie man das kgV findet, kannst du dir in diesem 📽 shorts Das kleinste gemeinsame Vielfache  ansehen.) Dann erweitern wir jeden Bruch, bei dem das nötig ist.

 \dfrac{1}{2} + \dfrac{3}{5} = \dfrac{5}{10} + \dfrac{6}{10} = \underline{\underline{ \dfrac{11}{10}}}

 \dfrac{x}{4} + \dfrac{3x}{2} = \dfrac{x}{4} + \dfrac{6x}{4} = \dfrac{7x}{4} = \underline{\underline{ \dfrac{7}{4}x}}

Brüche addieren

Gleichnamige Brüche addieren heißt, die Zähler addieren und den gemeinsamen Nenner beibehalten.

 \dfrac{3}{5} + \dfrac{4}{5} = \dfrac{3 + 4}{5} = \underline{\underline{\dfrac{7}{5}}}

Wie man Brüche addiert erkläre ich auch in diesem 📽 shorts Brüche addieren.

Brüche subtrahieren

Dabei gehen wir genauso vor wie bei der Addition.

 \dfrac{x}{3} - \dfrac{2x}{3} = \dfrac{x - 2x}{3} = \underline{\underline{- \dfrac{x}{3}}}

Brüche multiplizieren

Man multipliziert Brüche, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert.

 \dfrac{4}{7} \cdot 3 = \dfrac{4}{7} \cdot \dfrac{3}{1} = \dfrac{4 \cdot 3}{7 \cdot 1} = \underline{\underline{ \dfrac{12}{7}}} 
\dfrac{3}{4} \cdot \dfrac{x}{5} = \dfrac{3 \cdot x}{4 \cdot 5} = \dfrac{3x}{20} = \underline{\underline{\dfrac{3}{20}x}}

Eine ähnliche Aufgabe erkläre ich auch in diesem 📽 shorts Brüche multiplizieren.

Brüche dividieren

Man dividiert Brüche, indem man mit dem Kehrwert multipliziert.

 \dfrac{3}{8} : \dfrac{9}{4} = \dfrac{3}{8} \cdot \dfrac{4}{9} = \dfrac{4}{8} \cdot \dfrac{3}{9} = \dfrac{1}{2} \cdot \dfrac{1}{3} = \underline{\underline{\dfrac{1}{6}}} \newline
\dfrac{\frac{3a}{8b}}{\frac{9c}{2b}} = \dfrac{3a}{8b} : \dfrac{9c}{2b} = \dfrac{3a \cdot 2b}{8b \cdot 9c} = \dfrac{a}{4 \cdot 3c} = \underline{\underline{\dfrac{1}{12c}}}

Wie man Brüche dividiert erkläre ich auch in diesem 📽 shorts Brüche dividieren.

Beispiele:

  1. a)  \dfrac{\frac{2}{5}}{3} = \dfrac{2}{5} \cdot \dfrac{1}{3} = \underline{\underline{\dfrac{2}{15}}} 

b)  \dfrac{\frac{3}{7}}{t} = \dfrac{3}{7} \cdot \dfrac{1}{t} = \underline{\underline{\dfrac{3}{7t}}} 

c)  \dfrac{1}{\frac{3}{8}} = \underline{\underline{\dfrac{8}{3}}} 
  2. a)  \dfrac{1}{\frac{t}{4}} = \underline{\underline{\dfrac{4}{t}}} 

b)  \dfrac{1}{\frac{t}{2} + 1} = \dfrac{1}{\frac{t + 2}{2}} = \underline{\underline{\dfrac{2}{t + 2}}}

c)  \dfrac{-1 + 8t}{8} = \underline{\underline{- \dfrac{1}{8} + t}} 
  3. a)  \dfrac{-4}{2} = - \dfrac{4}{2} = \dfrac{4}{-2} = \underline{\underline{-2}}

b)  \dfrac{-x}{-a} = \underline{\underline{\dfrac{x}{a}}}

Beachte:

 \dfrac{0}{3} = 0 , aber  \dfrac{3}{0}  ist nicht definiert.

Hier findest du Aufgaben dazu und die Lösungen der Aufgaben.

Außerdem hier Aufgaben dazu I und  Lösungen der Aufgaben I.

Hier Aufgaben II und  die Lösungen II.

Nächster Theorieteil: Dezimalbrüche.

Hier findest du eine Übersicht über alle Beiträge zum Thema Bruchrechnen.
Und hier eine Übersicht über alle Beiträge zur Mathematik in der Sekundarstufe.

Ähnliche Beiträge