Hier findest du die Lösungen mit komplettem Lösungsweg zu den Bruchrechnen Aufgaben. Dabei sollst du Brüche addieren, subtrahieren, multiplizieren, dividieren, Brüche kürze, gleichnamig machen, aus gemischten Zahlen Brüche machen.
1. Addiere folgende Brüche. Falls nötig, mache sie vorher gleichnamig.
Mit anderen Worten: Dazu muss man die Brüche erweitern. Wie man Brüche erweitert und kürzt kannst du hier nachlesen oder dir auch in diesem 
Video Brüche erweitern ansehen.
a)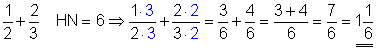 
Der Hauptnenner ist 6. Zuerst erweitern wir den ersten Bruch mit 3, den zweiten Bruch mit 2. Dann addieren wir die Zähler beider Brüche. Dadurch erhalten wir einen ein unechten Bruch, da der Zähler größer als der Nenner ist. Unechte Brüche können wir jedoch in der gemischten Schreibweise darstellen.
Diese Aufgabe erkläre ich auch in diesem shorts Brüche addieren.
b)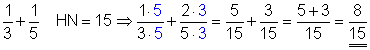 
Der Hauptnenner ist 15. Zuerst erweitern wir den ersten Bruch mit 5, den zweiten Bruch mit 3. Danach addieren wir die Zähler beider. Das Ergebnis ist hierbei ein echter Bruch, weil der Zähler kleiner als der Nenner ist.
c )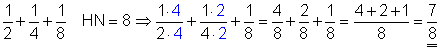 
Der Hauptnenner ist 8. Zuerst erweitern wir den ersten Bruch mit 4, den zweiten Bruch mit 2. Dann müssen wir den dritte Bruch nicht erweitern, da sein Nenner gleich dem Hauptnenner ist. Zuletzt addieren wir die Zähler aller Brüche.
d)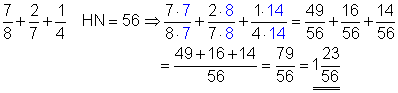 
Der Hauptnenner ist 56. Zuerst erweitern wir den ersten Bruch mit 7, den zweiten Bruch mit 8 und den dritten Bruch mit 14. Dann addieren wir die Zähler aller Brüche. Das Ergebnis ist ein unechter Bruch, weil der Zähler größer als der Nenner ist.
2. Subtrahiere folgende Brüche. Falls nötig, mache sie vorher gleichnamig
a)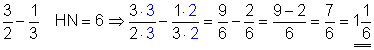 
Der Hauptnenner ist 6. Zuerst erweitern wir den ersten Bruch mit 3, den zweiten Bruch mit 2. Danach subtrahieren wir den Zähler des zweiten Bruchs vom ersten Bruch. Das Ergebnis ist ein unechter Bruch, weil der Zähler größer als der Nenner ist. Unechte Brüche kann man jedoch in der gemischten Schreibweise darstellen.
b) 
Der Hauptnenner ist 14. Zuerst erweitern wir den ersten Bruch mit 2, den zweiten Bruch mit 7. Danach subtrahieren wir den Zähler des zweiten Bruchs vom ersten Bruch. Das Ergebnis ist ein echter Bruch.
c)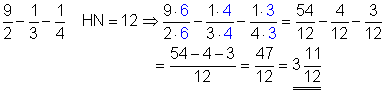 
Der Hauptnenner ist 12. Zuerst erweitern wir den ersten Bruch mit 6, den zweiten Bruch mit 4 und den dritten Bruch mit 3. Danach subtrahieren wir den Zähler des zweiten Bruchs und dritten Bruchs vom ersten Bruch. Das Ergebnis ist ein unechter Bruch, weil der Zähler größer als der Nenner ist. Unechte Brüche kann man jedoch in der gemischten Schreibweise darstellen.
d)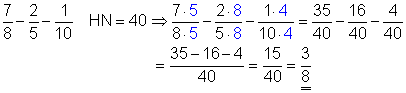 
Der Hauptnenner ist 40. Zuerst erweitern wir den ersten Bruch mit 5, den zweiten Bruch mit 8 und den dritten Bruch mit 4. Danach subtrahieren wir den Zähler des zweiten Bruchs und dritten Bruchs vom ersten Bruch. Das Ergebnis ist ein echter Bruch.
3. Multipliziere folgende Brüche. Falls möglich, kürze das Ergebnis
a)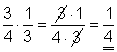 
Zähler und Nenner beider Brüche werden miteinander multipliziert. Man kann vor der Multiplikation die 3 heraus kürzen.
Diese Aufgabe erkläre ich auch in diesem shorts Brüche multiplizieren.
b) 
Zuerst multiplizieren wir Zähler und Nenner beider Brüche miteinander. Das Ergebnis können wir nicht weiter kürzen.
c) 
Wir multiplizieren wieder Zähler und Nenner beider Brüche miteinander. Das Ergebnis können wir durch 2 kürzen. Das ist ein unechter Bruch, den wir in der gemischten Schreibweise darstellen können.
d)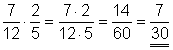 
Wir multiplizieren Zähler und Nenner beider Brüche miteinander. Das Ergebnis können wir durch 2 kürzen
4. Dividiere folgende Brüche. Falls möglich, kürze das Ergebnis
Wie man Brüche dividiert erkläre ich auch in diesem shorts Brüche dividieren.
a)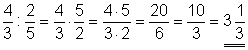 
Wir multiplizieren den ersten Bruch mit dem Kehrwert des zweiten Bruches. Das Ergebnis können wir durch 2 kürzen. Den unechten Bruch können wir in der gemischten Schreibweise darstellen.
b)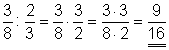 
c)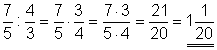 
d)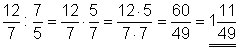 
5. Mache zuerst aus den gemischten Zahlen Brüche, dann löse die Aufgabe
a)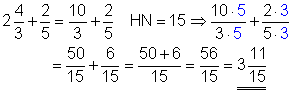 
Die erste Zahl ist ein gemischte Zahl, mit anderen Worten ein Bruch in gemischter Schreibweise. Die können wir in einen unechten Bruch mit gleichem Nenner zu verwandeln. Dazu multiplizieren wir die Zahl, die vor dem Bruch steht, mit dem Nenner und addieren sie zu dem Zähler. Für zwei vier drittel bedeutet das: 2 x 3 + 4 = 10. Danach rechnen wir nach der Regel für die Addition von Brüchen.
b)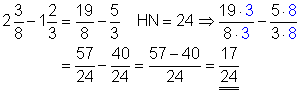 
Die gemischten Zahlen werden in Brüche verwandelt. Die weitere Rechnung erfolgt nach der Regel für die Subtraktion von Brüchen
c)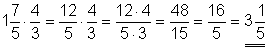 
Die gemischte Zahl wird in einen Bruch verwandelt. Die weitere Rechnung erfolgt nach der Regel für die Multiplikation von Brüchen
d)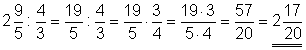 
Die gemischte Zahl wird in einen Bruch verwandelt. Die weitere Rechnung erfolgt nach der Regel für die Division von Brüchen
Hier findest du die Aufgaben.
Und hier die Theorie hierzu: Einführung in die Bruchrechnung
und Dezimalbrüche.
Weitere Aufgaben: Bruchrechnen Aufgaben I.
Hier findest du eine Übersicht über alle Beiträge zur Bruchrechnung, darin auch links zu weiteren Aufgaben.
Und hier eine Übersicht über alle Beiträge zur Mathematik in der Sekundarstufe I.
