Hier findest du die Lösungen der Aufgaben zur beschleunigten Bewegung II.
Im Beitrag Wie berechnet man Beschleunigung habe ich die Theorie ausführlich erklärt. Außerdem gibt es da viele Rechenbeispiele.
1. Rennwagen
Ein Rennwagen startet mit einer konstanten Beschleunigung von a = 5 m/s2.
a) Welche Geschwindigkeit wird nach 10 s erreicht? ( in m/s und km/h )
Die Aufgabe erkläre ich in diesem 📽 Video Geschwindigkeit berechnen mit Beschleunigung und Zeit.
b) Wie groß ist der in 10 s zurückgelegte Weg?
Die Aufgabe erkläre ich in diesem 📽 Video Strecke berechnen mit Beschleunigung und Zeit.
Hier habe ich erklärt, wie man die Geschwindigkeit berechnet.
Und hier habe ich erklärt, wie man wie man von \frac{km}{h} in \frac{m}{s} umrechnet und umgekehrt.
In diesem 📽 Video m/s in km/h umrechnen erkläre ich außerdem, wie man die Einheiten umrechnet.
Ausführliche Lösung:
a) Geschwindigkeit
Die Aufgabe erkläre ich in diesem 📽 Video Geschwindigkeit berechnen mit Beschleunigung und Zeit.
gegeben: a = 5\dfrac{m}{s^2} ; t = 10 s
gesucht: v in m/s und km/h
v = a · t = 5\dfrac{m}{s^2} · 10s = 5 · 10 \dfrac{m · s}{s · s} = 50\dfrac{m · \cancel s}{s · \cancel s} = \underline{\underline{50\dfrac{m}{s}}} \\ 1 \dfrac{m}{s} = 3,6 \dfrac{km}{h} \\ \\ 50\dfrac{m}{s} = 50 · 3,6 \dfrac{km}{h} = \underline{\underline{180\dfrac{km}{h}}}Nach 10 s erreicht der Rennwagen eine Geschwindigkeit von v = 50 m/s = 180 km/h.
b) Weg
gegeben: a = 5\dfrac{m}{s^2} ; t = 10 s gesucht: s
s = \dfrac{a · t^2}{2} = \dfrac{5\dfrac{m}{s^2} · (10s)^2}{2} = \dfrac{5\dfrac{m}{s^2} · 100 s^2}{2} = \dfrac{5 · 100 \dfrac{m · s^2}{s^2}}{2} = \dfrac{500 \dfrac{m · \cancel s^2}{\cancel s^2}}{2} = \dfrac{500m}{2} = \underline{\underline{250 m}}Der in 10 s zurückgelegte Weg beträgt 250 m.
2. Motorräder
Mit zwei Motorrädern wird ein Beschleunigungstest gemacht.
Motorrad Nr. 1 erreicht nach 10 s die Geschwindigkeit v = 100 km/h.
Motorrad Nr. 2 braucht eine Beschleunigungsstrecke von 100 m um auf die Endgeschwindigkeit von 100 km/h zu kommen.
Welches Motorrad erreicht die größten Beschleunigungswerte?
Hier habe ich ein ähnliches Beispiel für Motorrad 1 gerechnet.
Und hier für Motorrad 2.
Ausführliche Lösung:
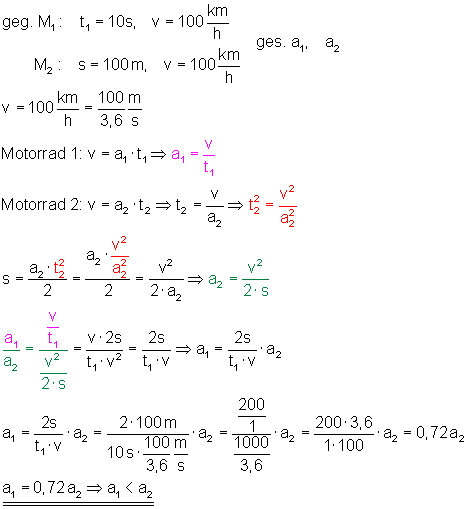
Motorrad 2 hat die größeren Beschleunigungswerte, denn a1 = 0,72a2.
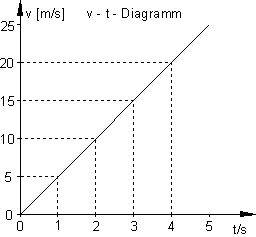
3. v-t-Diagramm
Zeichne ein v -t-Diagramm der gleichmäßig beschleunigten Bewegung für a = 5 m/s2.
Lese daraus die Geschwindigkeit nach der 1. 2. 3. und 4. Sekunde ab.
Ergebnis
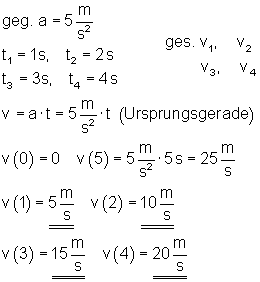
4. Flugzeug
Ein Flugzeug, dass zunächst mit einer gleichbleibenden Geschwindigkeit von 160 m/s fliegt, beschleunigt 15 s lang mit a = 6,5 m/s2.
Welche Geschwindigkeit hat es dann?
Ausführliche Lösung
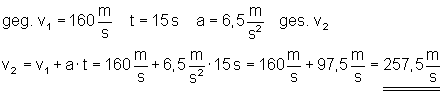
Nach der Beschleunigungsphase hat das Flugzeug eine Geschwindigkeit von v = 257,5 m/s.
5. Motorrad
Ein Motorrad erreicht bei konstanter Beschleunigung aus der Ruhe nach 45 m Weg die Geschwindigkeit 30 m/s.
Wie lange braucht es , wie hoch ist die Beschleunigung?
Diese Aufgabe habe ich in diesem 📽 Video Zeit und Beschleunigung berechnen aus Geschwindigkeit und Weg erklärt.
Außerdem findet ihr hier alle Formeln zur Beschleunigung.
gegeben: Strecke s = 45 m; Geschwindigkeit v = 30 m/s
gesucht: Zeit t; Beschleunigung a
t = \dfrac{v}{a} \Rightarrow \dfrac{30 \dfrac{m}{s} }{ 10\dfrac{m}{s^2} } = \dfrac{30}{10} · \dfrac{m}{s} · \dfrac{s^2}{m} = 3 \dfrac{\cancel m · \cancel s · s }{\cancel s · \cancel m} = \underline{\underline{3 s}}
Eine andere Lösung:
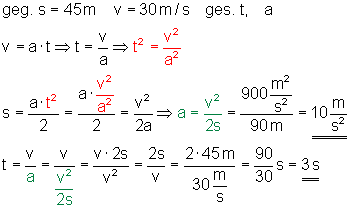
Das Motorrad braucht t = 3 s. Die Beschleunigung beträgt a = 10 m/s2.
6. In 3 Sekunden
Nach 3 Sekunden erreicht ein Fahrzeug die Geschwindigkeit 0,52 m/s.
Wie groß ist der in 3 s zurückgelegte Weg?
Hier habe ich erklärt, wie man die Strecke berechnet.
Ausführliche Lösung
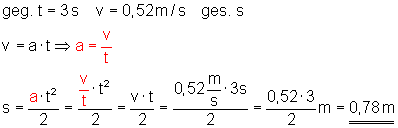
Der in 3 Sekunden zurückgelegte Weg beträgt s = 0,78 m.
7. Radfahrerin
Eine Radfahrerin startet gleichmäßig beschleunigt aus dem Stand.
Nach 5 s hat sie 20 m zurückgelegt. Wie groß ist die Beschleunigung?
Ausführliche Lösung
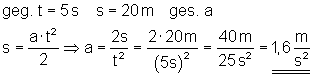
Die Beschleunigung beträgt 1,6 m/s2.
8. Zug
Ein Zug erreicht aus der Ruhe nach 10 s die Geschwindigkeit 5 m/s.
Wie weit ist er gefahren?
Ausführliche Lösung
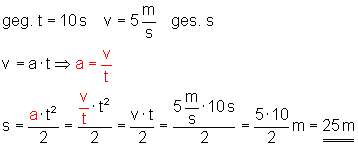
Der Zug ist s = 25 m weit gefahren.
9. Anfahrender Wagen
Ein mit konstanter Beschleunigung anfahrender Wagen kommt in den ersten 12 s 133 m weit.
Wie groß sind Beschleunigung und Geschwindigkeit nach 12 s?
Ausführliche Lösung
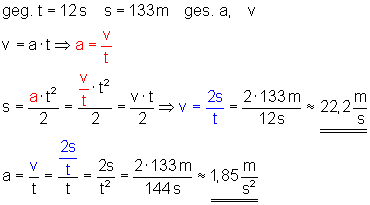
Die Beschleunigung beträgt etwa 1,85 m/s2.
Die Geschwindigkeit beträgt etwa 22,2 m/s.
10. Achterbahn
Die Achterbahn „Millennium Force (USA)“ beschleunigt bei ungebremster Abfahrt in 3,9 s von 28,8 km/hauf 110,7 km/h.
a) Wie groß ist die Beschleunigung (sie soll als konstant angenommen werden)?
b) Wie lang ist der Beschleunigungsweg?
Ausführliche Lösung
a) Beschleunigung
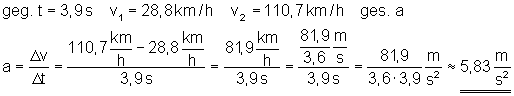
Die Beschleunigung beträgt etwa 5,83 m/s2.
b) Beschleunigungsweg
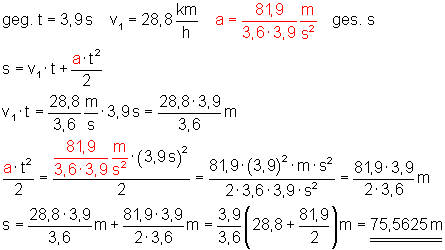
Der Beschleunigungsweg beträgt s = 75, 5625 m.
11. Pfeil
Ein Pfeil wird von der Sehne eines Bogens auf einer Strecke von 0,6 m beschleunigt. Er erreicht eine Geschwindigkeit von 60 m/s.
a) Warum ist die Beschleunigung nicht konstant?
b) Wie groß ist die mittlere, konstant angenommene Beschleunigung?
c) Wie lange dauert der Beschleunigungsvorgang?
Ausführliche Lösung
a) Warum ist die Beschleunigung nicht konstant?
Die Beschleunigung ist nicht konstant, da sich die Kraft, die die Sehne auf den Pfeil ausübt, ändert.
b) Mittlere Beschleunigung
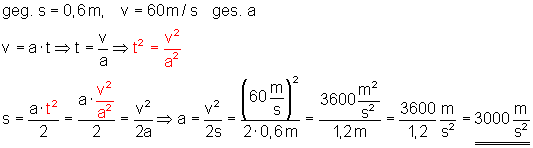
Die mittlere Beschleunigung beträgt 3000 m/s2.
c) Wie lange dauert der Beschleunigungsvorgang?
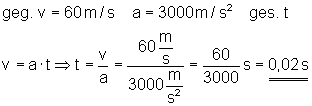
Der Beschleunigungsvorgang dauert t = 0,02 s.
12. Körper
Ein Körper legt in der ersten Sekunde aus der Ruhe heraus 20 cm, in er 2. Sekunde 60 cm, in der 3. Sekunde 100 cm zurück.
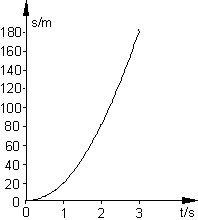
a) Skizziere ein s-t-Diagramm.
b) Welche Bewegung liegt vor?
c) Welche Geschwindigkeit hat der Körper nach 1s, 2s, 3s?
d) Wie groß ist die mittlere Geschwindigkeit für den gesamten Weg?
Ausführliche Lösung
a) s-t-Diagramm
Nach der 1. Sekunde wurden 20 cm,
nach der 2. Sekunde 20 cm + 60 cm = 80 cm
und nach der 3. Sekunde 80 cm + 100 cm = 180 cm zurückgelegt.
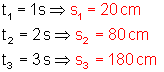
b) Welche Bewegung liegt vor?
Vermutung: Gleichmäßig beschleunigte Bewegung.
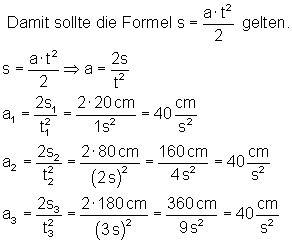
Da in allen drei Fällen die Beschleunigung a = konstant ist, handelt es sich tatsächlich um eine gleichmäßig beschleunigte Bewegung.
c) Welche Geschwindigkeit hat der Körper nach 1s, 2s, 3s?
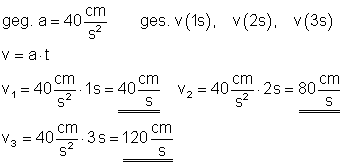
d) mittlere Geschwindigkeit
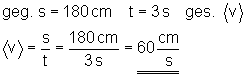
Die mittlere Geschwindigkeit beträgt <v> = 60 cm/s.
Hier findest du die Aufgaben.
Ähnliche Aufgaben mit anderen Werten.
Hier die Theorie zur Beschleunigung.
Und hier geht es um Beschleunigung aus der Bewegung und Bremsweg.
Und hier eine Übersicht über weitere Beiträge zum Thema Mechanik und Elektronik, darin auch Links zu Aufgaben.
Außerdem kannst du den Wikipediaartikel zur Beschleunigung lesen.