Bis jetzt haben wir den Flächeninhalt einfacher Flächen ermittelt, das heißt zwischen einem Graphen und der x-Achse. Manchmal müssen wir den Inhalt einer Fläche berechnen, die zwischen zwei Funktionsgraphen liegt. Dazu berechnet man die Differenz der Flächen zwischen den jeweiligen Funktionen mit der x-Achse. Zuerst stelle ich ein anschauliches Beispiel vor. Danach erkläre ich die Berechnung. Anschließend betrachte ich den Fall, dass eine Funktion unterhalb der x-Achse liegt. Dann beschreibe ich die allgemeine Formel zur Berechnung der Fläche zwischen zwei Funktionen. Die Vorgehensweise dazu erkläre ich anhand eines ausführlichen Beispiels.
Wenn du hier klickst, kommst du zu den Aufgaben.
- Grundsätzliches zur Fläche zwischen Funktiosngraphen
- Berechnung der Fläche zwischen Funktionsgraphen, zwei Methoden:
- 1. Zwei Funktionen integrieren und die Flächen subtrahieren
- 2. Zwei Funktionen subtrahieren und die neue Funktion integrieren
- Formel zur Berechnung der Fläche zwischen zwei Funktionen
- Beispiel zur Berechnung der Flächen zwischen Funktionsgraphen
- Berechnung mit einem Taschenrechner mit Speicherfunktion
- Aufgaben: Flächen zwischen Funktionsgraphen
Grundsätzliches zur Fläche zwischen Funktionsgraphen
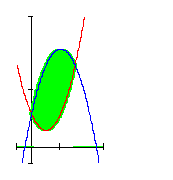
Wir wollen die Fläche A zwischen zwei Funktionsgraphen ermitteln.
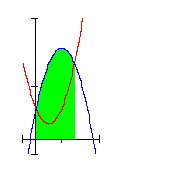
Dazu brauchen wir die Fläche zwischen der 1. Funktion und der x-Achse A1.
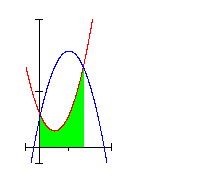
Außerdem die Fläche zwischen der 2. Funktion und der x-Achse A2.
Also kann man die Fläche zwischen zwei Funktionsgraphen wie folg berechnen: A = A1 – A2.
Berechnung der Fläche zwischen Funktionsgraphen
Dafür stelle ich im folgenden zwei Methoden vor.
1. Zwei Funktionen integrieren und die Flächen subtrahieren
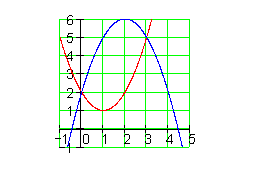
Dabei gehen wir so vor:
1. Zuerst bestimmen wir die x-Koordinaten der Schnittpunkte der beiden Graphen. Dazu setzen wir die beiden Funktionen gleich. Vo der dabei entstandenen Funktion suchen wir die Nullstellen. Diese Nullstellen sind auch die Schnittpunkte der beiden Funktionen. Dann haben wir die Integrationsgrenzen, mit denen wir arbeien.
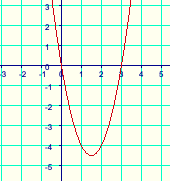
2. Als nächstes bilden wir die Integrale beider Funktionen in diesen Grenzen.
3. Schließlich subtrahieren wir die kleinere Fläche von der größeren.

2. Zwei Funktionen subtrahieren und die neue Funktion integrieren
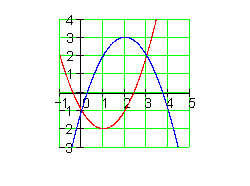
Dafür verschieben wir die Graphen der beiden Funktionen längs der y-Achse um drei Einheiten nach unten und berechnen den Flächeninhalt neu. Wie wir im letzten Beitrag gesehen haben, hängt das Vorzeichen des Ergebnisses einer Flächenberechnung davon ab, ob die Fläche oberhalb oder unterhalb der x-Achse liegt. Wir untersuchen nun, ob das einen Einfluss auf die Berechnung im obigen Beispiel hat. Aus der Anschauung heraus sollte das Ergebnis gleich sein. Auch die x-Werte der Schnittpunkte und somit die Integrationsgrenzen bleiben unverändert.
1. Zuerst subtrahieren wir die eine Funktion von der anderen. Dabei stellen wir fest, dass die neue Funktion 2x^2-6x=0 die gleiche ist wie bei der ersten Methode. Dadurch, dass wir den Graphen nach unten verschieben, ändert sich die Fläche nicht.

2. Als nächstes integrieren wir die neue Funktion. Falls das Ergebnis negativ ist, bilden wir den Betrag. Denn eine Fläche kann nur positiv sein.

Dazu kannst du dir das 📽️Video Integral Fläche zwischen Graphen ansehen.
Formel zur Berechnung der Fläche zwischen zwei Funktionen
Die zweite Methode ist also schneller und einfacher. Deshalb können wir festlegen wie man die Fläche zwischen Funktionsgraphen berechnet:

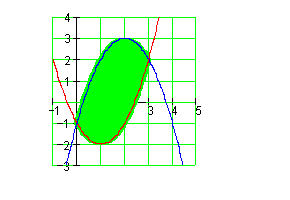
Beispiel zur Berechnung der Flächen zwischen Funktionsgraphen
Dazu stelle ich ein Beispiel zur Verfügung. Zuerst zeichnen wir beide Graphen in ein Koordinatensystem. Die Integrationsgrenzen sind die x-Koordinaten der Schnittpunkte beider Graphen.
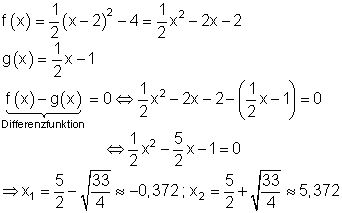
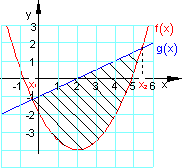
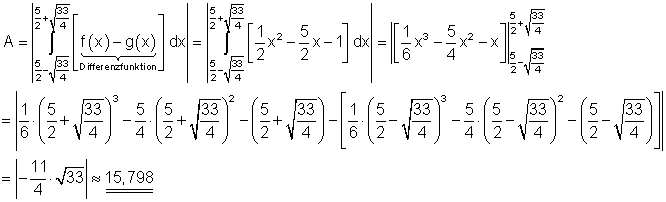
Die Fläche zwischen den beiden Graphen beträgt etwa 15,798 FE.
Bemerkung:
Man kann die Rechnung auch ohne Beträge durchführen, wenn man von dem Ergebnis, falls es negativ ist, den Betrag bildet.
Falls f(x) im Integrationsintervall [ a ; b ] oberhalb von g(x) liegt, ist das Ergebnis positiv.
Falls f(x) im Integrationsintervall [ a ; b ] unterhalb von g(x) liegt, ist das Ergebnis negativ.
Berechnung mit einem Taschenrechner mit Speicherfunktionen
Nachfolgend zeige ich, wie man obige Rechnung mit einem Taschenrechner mit Speicherfunktionen durchführt.
Zum Beispiel mit dem TI- 30 eco RS von Texas Instruments.
Lösen Sie das bestimmte Integral:
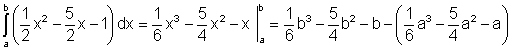
Wir speichern die Integrationsgrenzen a und b im Taschenrechner. Dann berechnen wir den algebraische Ausdruck.

Aufgaben: Flächen zwischen Funktionsgraphen
Bestimme die Fläche zwischen folgenden Funktionsgraphen. Zeichne danach beide Graphen in ein Koordinatensystem. Schraffiere schließlich die berechnete Fläche.
Dazu kannst du dir das 📽️Video Integral Fläche zwischen Graphen ansehen.
1.![]()
2.![]()
3.![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
9.![]()
10.![]()
Dazu findest du hier die Lösungen.
Und hier eine Übersicht über weitere Beiträge zum Thema Integralrechnung, darin auch Links zur Theorie und zu weiteren Aufgaben.



