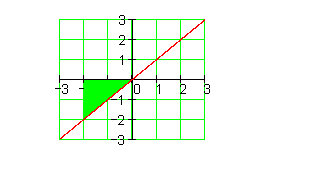Im letzten Beitrag haben wir gesehen, wie wir die Wiese aus dem Einführungsbeispiel mit Hilfe der Integralrechnung berechnen können. Hier zeige ich wie man die Fläche einfacher Flächen in der Integralrechnung berechnen kann. Zuerst demonstriere ich anhand eines anschaulichen Beispiels, wie man bei einer Funktion 1. Grades die Fläche zwischen f(x) und der x-Achse mittels Integration berechnet. Dabei sehen wir, dass Flächen oberhalb der x-Achse positive Werte ergeben, unterhalb der x-Achse negative Werte. Dazu gibt es ein Video. Danach erkläre ich das Gleiche bei einer Funktion 2. Grades. Dann wird der Zusammenhang zwischen Flächenlage und Vorzeichen klar. Anschließend untersuche ich, was geschieht, wenn die Integrationsgrenzen vertauscht werden. Bevor ich Trainingsaufgaben zur Verfügung stelle, zeige ich den Rechenweg anhand eines Beispiels.
1. Beispiel Fläche oberhalb der x-Achse berechnen
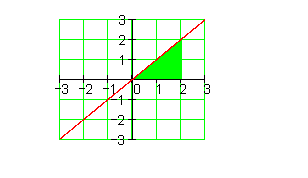
Nehmen wir zuerst die einfachste lineare Funktion f(x)=x. Wir berechnen die Fläche zwischen f(x) und der x-Achse im Intervall 0≤x≤2 folgendermaßen:
\int \limits_{0}^{2} f(x) \,dx = \int \limits_{0}^{2} x \,dx = \frac{x^2}{2} \big|_{0}^{2}=\frac{2^2}{2}-\frac{0^2}{2}= \frac{4}{2}= \underline{\underline{2FE}}
2. Beispiel Fläche unterhalb der x-Achse berechnen
Als nächstes berechnen wir die Fläche im Intervall -2≤x≤0:
\int \limits_{-2}^{0} f(x) \,dx = \int \limits_{-2}^{0} x \,dx = \frac{x^2}{2} \big|_{-2}^{0}=\frac{0^2}{2}-\frac{(-2)^2}{2}= 0-\frac{4}{2}= \underline{\underline{-2FE}}
Eine negative Fläche ist merkwürdig, aber dadurch wissen wir, dass sie unterhalb der x-Achse ist. Positive Flächen sind oberhalb der x-Achse.
3. Beispiel Fläche über den Nullpunkt hinaus berechnen
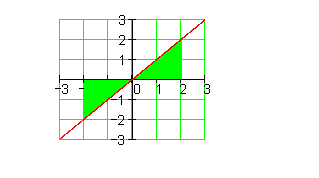
Schließlich berechnen wir die Fläche im Intervall -2≤x≤2:
\int \limits_{-2}^{2} f(x) \,dx = \int \limits_{-2}^{2} x \,dx = \frac{x^2}{2} \big|_{-2}^{2}=\frac{2^2}{2}-\frac{(-2)^2}{2}= \frac{4}{2}-\frac{4}{2}= \underline{\underline{0FE}}
Das kann wirklich nicht stimmen! Deshalb dürfen wir Flächen immer nur bis zu einem Nullpunkt berechnen. Wenn wir eine Fläche darüber hinaus berechnen wollen, dann müssen wir das Integral aufteilen und mit Beträgen rechnen.
\int \limits_{-2}^{2} f(x) \,dx = \big \vert \int \limits_{-2}^{0} x \,dx \big \vert +\big \vert \int \limits_{0}^{2} x \,dx \big \vert = \big \vert\frac{x^2}{2} \big|_{-2}^{0}\big \vert + \big \vert\frac{x^2}{2} \big|_{0}^{2}\big \vert=\big \vert\frac{0^2}{2} - \frac{(-2)^2}{2}\big \vert + \big \vert\frac{2^2}{2} - \frac{0^2}{2}\big \vert= 2+2= \underline{\underline{4FE}}
Weil man weiß, dass Flächen immer positiv sind, können wir auch einfach beide Flächen berechnen und danach die Beträge davon bilden.
Dazu kannst du dir das 📽️Video Fläche unter x-Achse Integralrechnung ansehen.
4. Beispiel

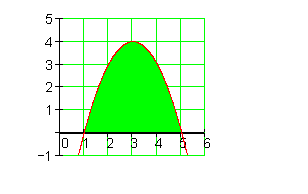
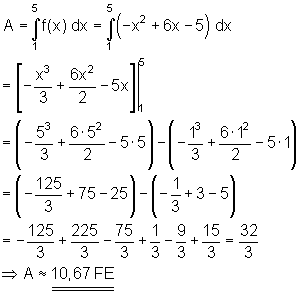
5. Beispiel

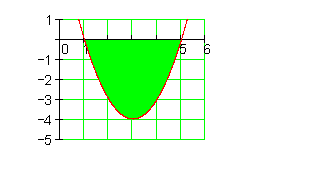
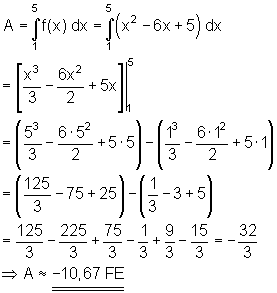
Zusammenhang zwischen Flächenlage und Vorzeichen:

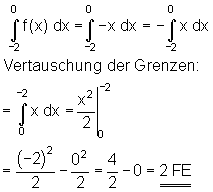
Vertauschung der Integrationsgrenzen
Was geschieht, wenn die Integrationsgrenzen vertauscht werden?
6. Beispiel

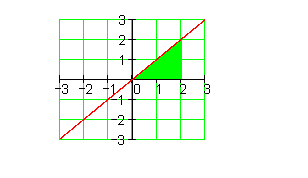

7. Beispiel

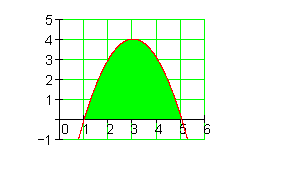
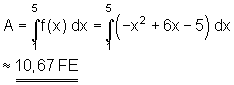

Satz Vertauschen der Integrationsgrenzen

8. Beispiel
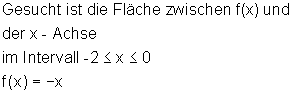
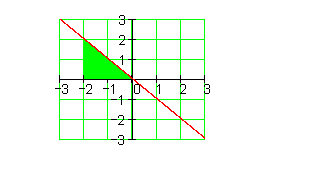
Ausführliches Beispiel zur Flächenberechnung Integralrechnung:
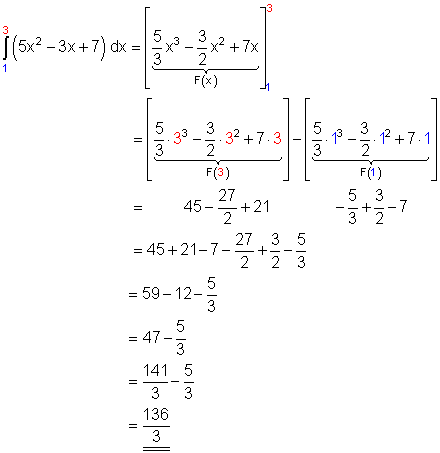
Aufgaben Flächenberechnung Integralrechnung
Bevor du anfängst zu üben, stelle ich die Vorgehensweise anhand eines ausführlichen Beispiels vor:
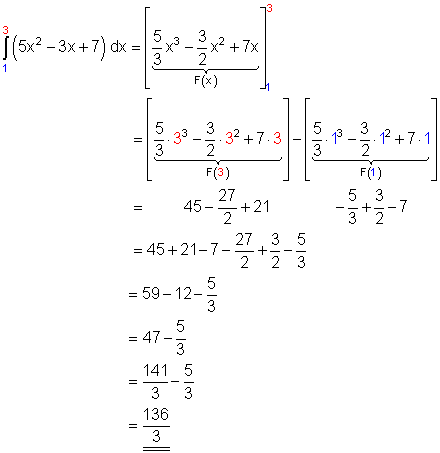
Berechne folgende bestimmte Integrale:
1. ![]()
2. 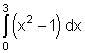
3. 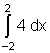
4. ![]()
5. 
6. 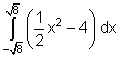
7. 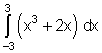
8. 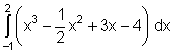
9. 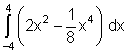
10. 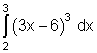
Hier findest du die Lösungen Integralrechnung II.
Und hier eine Übersicht über alle Beiträge zur Integralrechnung, darin auch Links zur Theorie und zu weiteren Aufgaben.