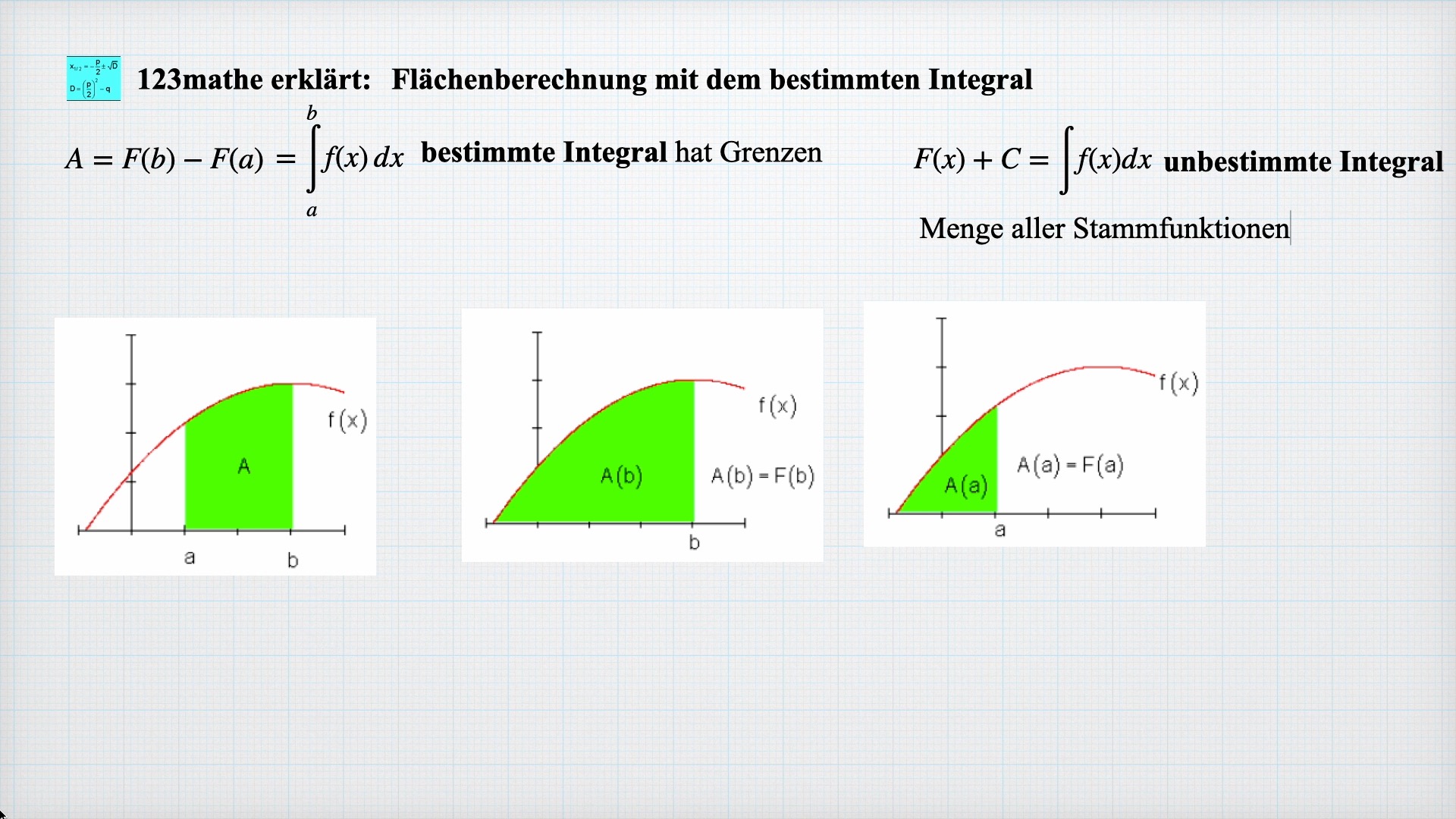
In diesem Beitrag erkläre ich, wie man vom Integral unbestimmten zum bestimmten Integral kommt.
Vorbetrachtungen
Im letzten Beitrag haben gesehen, wenn zu einer Funktion f(x) eine Stammfunktion F(x) ermittelt werden kann, so existieren unendlich viele Stammfunktionen, die sich nur durch eine additive Konstante C voneinander unterscheiden.
Beispiel:

Definition unbestimmtes Integral:
Der Zusammenhang zwischen der Differenzial – und Integralrechnung können wir mit folgendem Satz beschreiben:
Satz unbestimmtes Integral:
 .
.
Zur Flächenberechnung mit dem bestimmten Integral
Wenn wir nun die Fläche unter dem Funktionsgraphenzwischen in den Intervallgrenzen [ a ; b ] bestimmt wollen,
so können wir dazu die bisherigen Erkenntnisse auf unser Problem anwenden .
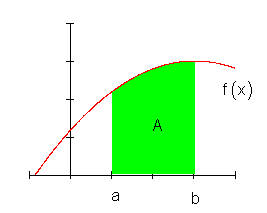
Die Überlegungen nach der Existenz einer Flächenfunktion führten uns zu folgender Erkenntnis:
Es besteht eine Beziehung zwischen
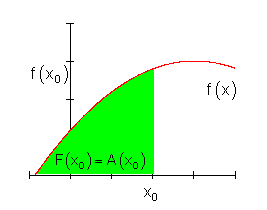
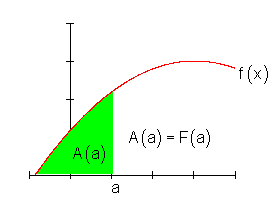
1. der Fläche unter dem Funktionsgraphen der betrachteten Funktion f(x) bis zur Stelle x0 und
2. einer Funktion F(x), in der die Ableitung der Funktion F(x) an der Stelle x0 gleich dem Funktionswert der Funktion f an der Stelle x0 ist.
![]()
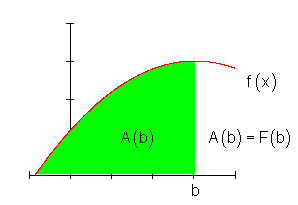
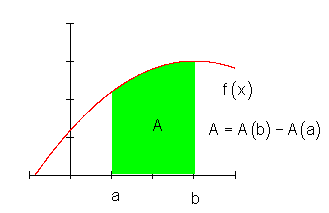
Die Fläche zwischen den Intervallgrenzen [ a ; b ] lässt sich ermitteln aus der Differenz der Fläche unter dem Funktionsgraphen an der Stelle.

Satz:
Dazu könnt ihr euch das 📽️Video Bestimmtes unbestimmtes Integral ansehen. Das ist der erste Teil des 📽️ Video Bestimmtes Integral Flächenberechnung.
Jetzt versuchen wir mit den bisherigen Erkenntnissen noch einmal die Fläche der Wiese aus dem Einführungsbeispiel zu berechnen.
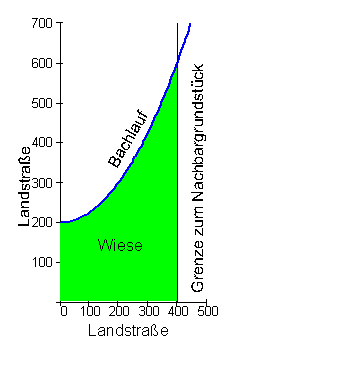

Dazu kansst du dir das 📽️Video Bestimmtes Integral mit F(x) berechnen ansehen. Das ist der zweite Teil des 📽️ Video Bestimmtes Integral Flächenberechnung .
Die Konstante fällt bei der Subtraktion heraus. In der Praxis hat sich für die Lösung dieses Problems eine andere Schreibweise bewährt:
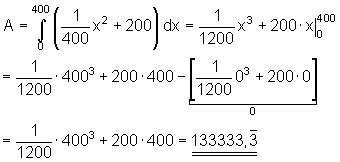
Dazu könnt ihr euch dieses 📽️ Video Bestimmtes Integral Flächenberechnung ansehen. Wenn ihr nur den dritten Teil mit dem Integralzeichen sehen wollt: 📽️Video Bestimmtes Integral mit Integralzeichen berechnen.
Im nächsten Berechnung einfacher Flächen werden wir uns ansehen, wie man einfache Flächen grundsätzlich berechnet und dazu wieder die Integralrechnung einsetzen.
Hier findest du eine Übersicht über weitere Beiträge zum Thema Integralrechnung, dort auch Links zu weiteren Aufgaben.