Nachdem wir uns intensiv mit der Differentialrechnung beschäftigt haben, gebe ich hier eine Einführung in die Integralrechnung. Während die Differentialrechnung eingesetzt wird, um Grenzwerte wie zum Beispiel den maximalen Gewinn zu berechnen, wird die Integralrechnung zur Flächenberechnung eingesetzt. Die Integralrechnung ist sozusagen die Umkehrung der Differentialrechnung.
Als erstes werde ich dies anhand eines praktischen Beispiels veranschaulichen, erst im nächsten Beitrag die Flächenfunktion erklären.
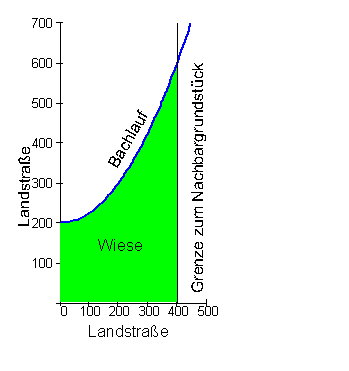
Integralrechnung Beispiel: Eine Wiese soll verkauft werden
Die abgebildete Wiese soll verkauft werden. Sie wird oben von einem Bachlauf, links und unten von einer Landstraße und rechts von dem Nachbargrundstück begrenzt.
Um die Wiese verkaufen zu können, müssen wir nun die Fläche ermittelt.
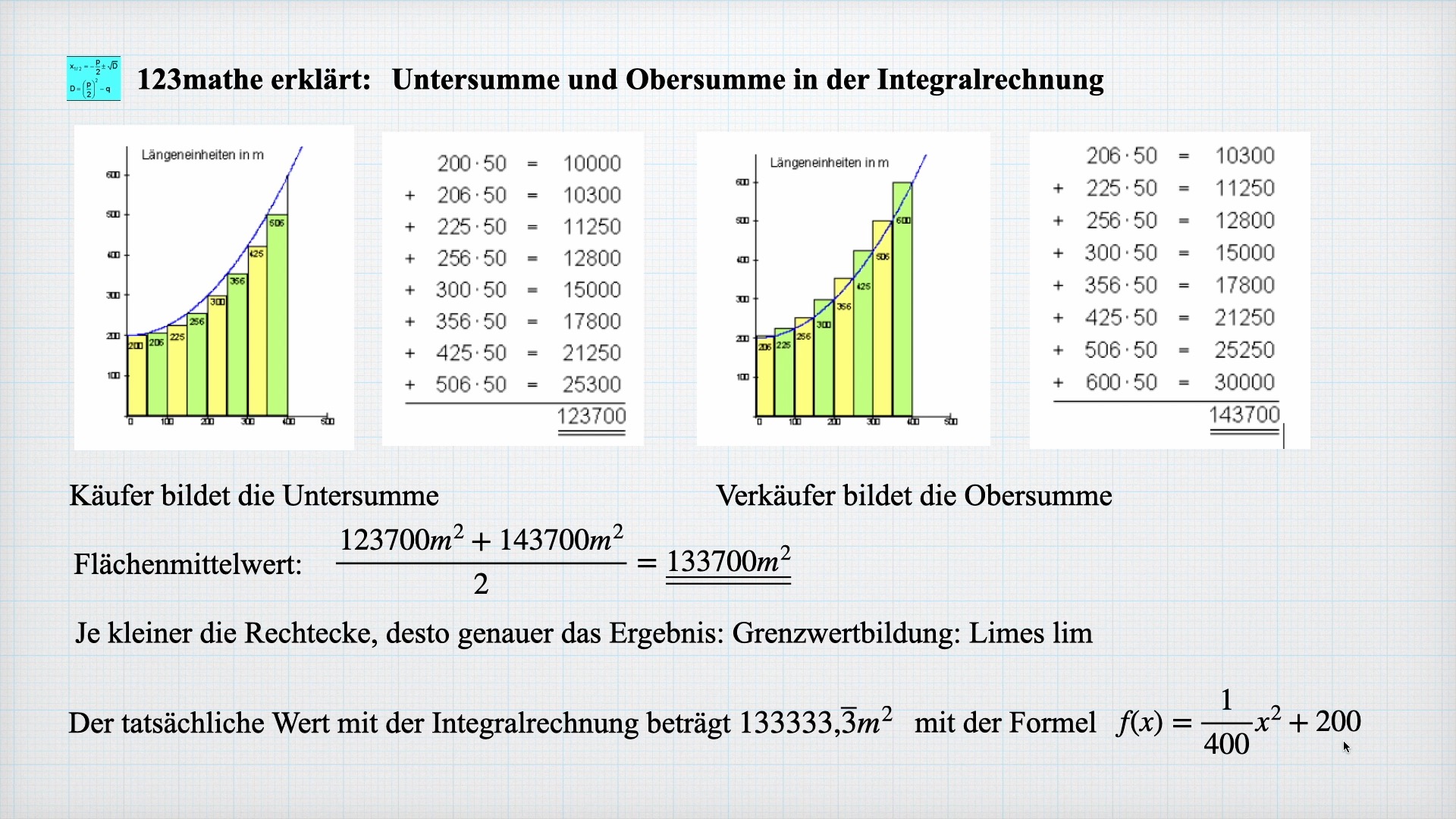
Beispiel für das Berechnen der Untersumme in der Integralrechnung:
Als erstes ermittelt der Käufer für sich die Fläche. Weil die krumme Fläche schwer zu berechnen ist, unterteilt er sie in Recktecke. Jeder Streifen ist 50 m breit und hat die in der Zeichnung angegebene Höhe. Dabei behält er aber im Hinterkopf, dass er möglichst wenig bezahlen will. Die Streifenflächen werden anschließend zusammengezählt. Deshalb wählt er Rechtecke unterhalb des Baches.
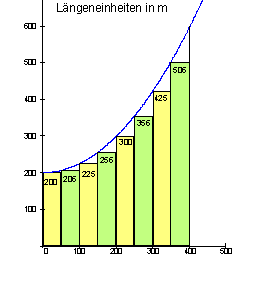
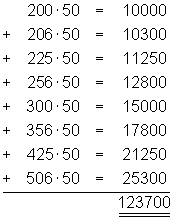
Für den Käufer ergibt sich somit eine Gesamtfläche von etwa 123700 m2
Beispiel für das Berechnen der Obersumme:
Der Verkäufer soll die Fläche auch möglichst genau, aber keinesfalls zu klein angeben.
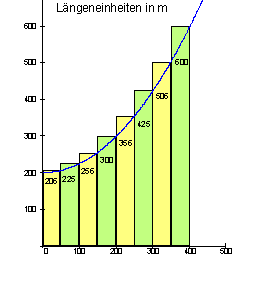
Auch er unterteilt die Wiese in Rechtecke, die 50 m breit sind. Allerdings haben die Streifen eine andere Höhe, wie man in der Zeichnung sehen kann. Die Streifenflächen werden auch hier zusammengezählt.
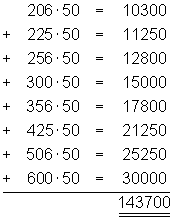
Für den Verkäufer ergibt sich somit eine Gesamtfläche von etwa 143700 m2.
Nachdem nun Verkäufer und Käufer jeweils die Fläche bestimmt haben, kommen beide zusammen und müssen sich über die zu bezahlende Fläche einig werden. Beide könnten sich in der „Mitte“ treffen, das bedeutet, dass sie beide den errechneten Mittelwert akzeptieren.
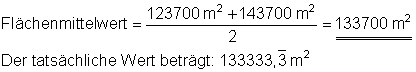
Was der Käufer gemacht hat, nennt man die Untersumme bilden.
Was der Verkäufer gemacht hat, nennt man die Obersumme bilden.
Der tatsächliche Flächenwert liegt irgendwo dazwischen.
![]() .
.
Dazu kannst du dir das 📽️Video Obersumme Untersumme in der Integralrechnung ansehen.
Im nächsten Beitrag werden wir ein Verfahren entwickeln, diesen Wert genau zu berechnen. Schritt für Schritt werde ich die Flächeninhaltsfunktion erklären.
Dort gibt es dann auch Aufgaben mit ausführlichen Lösungen dazu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Integralrechnung.