Nachdem wir uns intensiv mit der Kurvendiskussion beschäftigt haben, können wir nun sehen, wie es in der Kostenrechnung eingesetzt wird. Zuerst erkläre ich einige Begriffe, danach stelle ich ein konkretes Beispiel vor. Dazu gibt es ein Video.
Begriffe der Kostenrechnung
Gesamtkosten (Ertragliche Kostenfunktion) sind die in einem Betrieb bei der Produktion eines Produktes entstehenden Kosten.
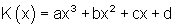
Stückkosten sind die Gesamtkosten pro Stück![]()
Fixkosten sind die Kosten, die auch dann entstehen, wenn nichts produziert wird. Z. B. Zinsen, Mieten, Versicherungen, Gehälter.
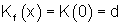
Variable Gesamtkosten sind die Gesamtkosten ohne Fixkosten
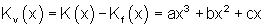
Variable Stückkosten sind die variablen Kosten pro Stück
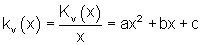
Grenzkosten oder Differentialkosten sind die Ableitung der Kostenfunktion K(x).
Die Grenzkosten beschreiben dabei den Kostenzuwachs bei einer Steigerung der Ausbringungsmenge um eine hinreichend kleine Menge.
Mit anderen Worten bedeuten die Grenzkosten K'(x1) die Steigung der Tangente an die Kostenkurve an der Stelle x1![]()
Das Betriebsminimum befindet sich im Minimum der variablen Stückkosten, dort gilt also K'(x) = kv(x).
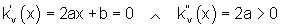
Die lineare Erlösfunktion: Preis p mal Ausbringungsmenge x.![]()
Gewinnfunktion = Erlösfunktion – Gesamtkosten.![]()
Beispiel zur Kostenrechnung
Betriebliche Daten:
Gesamtkosten:![]()
Fixkosten: Kf (x)= 420 GE (GE: Geldeinheiten)
Variable Stückkosten: kv(x) = 300 GE/ME bei einer Ausbringung von x = 10 ME (ME: Mengeneinheiten)
Betriebsminimum kv (x) = 200 GE bei einer Ausbringung von x = 5 ME
a) Stelle die Kostenfunktionsgleichung dazu auf!
b) Bei 15 ME decken die Erlöse die Kosten ( E(x) = K(x) ).
Bestimme dann unter der Voraussetzung, dass eine lineare Erlösfunktion gegeben ist, den Absatzpreis.
c) Bestimme die Gewinnzone.
d) Bestimme das Gewinnmaximum.
e) Zeichne die Graphen für K(x) ; G(x) ; kv(x) und E(x) in ein Koordinatensystem.
a) Aufstellen der Kostenfunktion:
Wir haben vier Unbekannte: a, b, c und d.
Fixkosten: Kf (x)= 420 GE (GE: Geldeinheiten). Die Variable, die fix ist, ist d, deshalb d = 420. Jetzt nur noch drei Unbekannte und drei Gleichungen:
Variable Stückkosten: kv(x) = 300 GE/ME bei einer Ausbringung von x = 10 ME (ME: Mengeneinheiten). Variable ist der Teil der Gleichung ohne d. Folglich: kv(10)=300: Gleichung I.
Betriebsminimum kv (x) = 200 GE bei einer Ausbringung von x = 5 ME. Also kv(5)=200: Gleichung II. Außerdem ist das Minimum die Ableitung von K(x), also ist K'(x) = 200: Gleichung III.
Die drei Gleichungen lösen wir dann mit dem Gauss-Verfahren.

Dazu kannst du dir das 📽️ Video Kostenfunktion aufstellen ansehen.
b) Der Absatzpreis
Als nächstes suchen wir den Absatzpreis p. Unter der Voraussetzung dass der Erlös die Kosten deckt, gilt: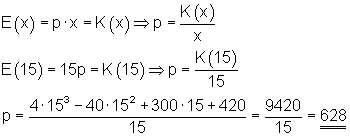
Der Absatzpreis beträgt 628 GE.
c) Die Gewinnzone
Die Gewinnzone beginnt dort, wo der Erlös E(x) > die Kosten K(x). Bei einem Absatzpreis von 628 GE rechnen wir also: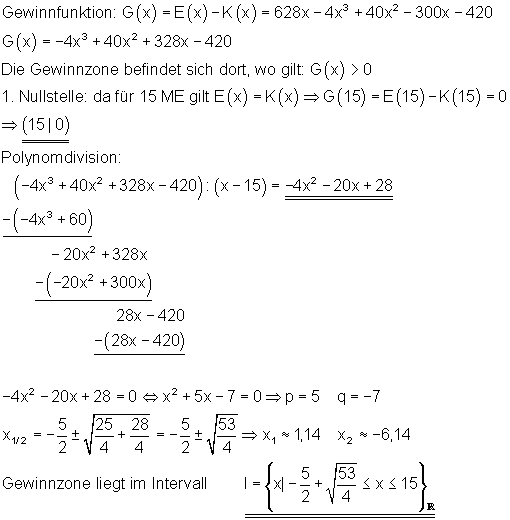
d) Das Gewinnmaximum in der Kostenrechnung
Der Gewinn G(x) ist dort am größten, wo die Ableitung von G(x) ein Maximum hat. Das heißt, wo G'(x) = 0 und G“(x) ≠0.
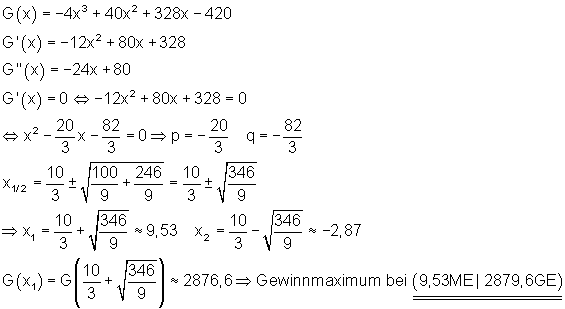
e) Die Graphen
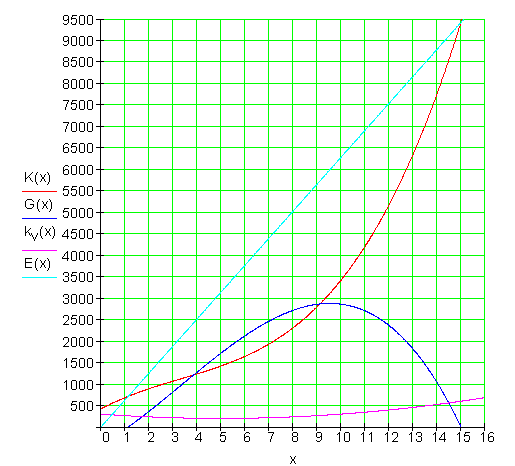
![]()
Dazu findest du hier die Theorie: Kurvendiskussion mit Beispielen.
Außerdem hier Aufgaben Differenzialrechnung XI.
Weitere Aufgaben zur Kurvendiskussion, komplette Klassenarbeiten, die Aufgaben Differenzialrechnung III, V, X und weitere Unterrichtsmaterialien könnt ihr hier kaufen.


