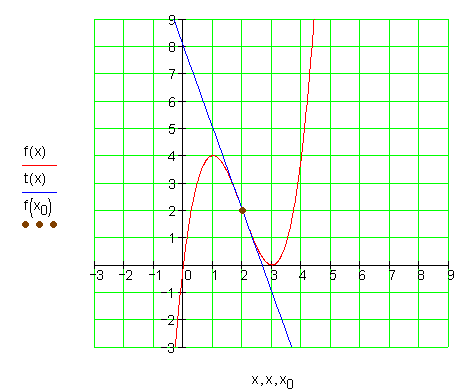
Aufgaben und Lösungen zur Tangente
Hier findest du Aufgaben und Lösungen zur Tangente. Zuerst gebe ich noch ein paar Erklärungen und Tipps zum Vorgehen. Überblick: Mit Klick auf einen der Punkte gelangst du sofort dorthin. 1. Tipps zum Lösen der Aufgaben zur Tangente: Um die Aufgaben zur Tangente zu verstehen, ist folgendes wichtig:Die Steigung des Graphen einer Funktion f(x) in […]
Aufgaben und Lösungen zur Tangente Weiterlesen »