Hier findest du Aufgaben zur Differenzialrechnung I, mit denen du dich auf eine Klassenarbeit vorbereiten kannst. In den Lösungen erkläre ich auch, wie man zu dem Ergebnis kommt. Viel Erfolg!
1. Parabel durch 3 Punkte.
a) Bestimme die Funktionsgleichung f(x) der Parabel, die durch die Punkte
![]()
Mit den drei Punkten stellen wir drei Gleichungen mit drei Variablen auf. Dann lösen wir dies mit nach Gauss. Dazu kannst du dir das Video 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.
b) Bestimme die Koordinaten des Scheitelpunktes.
c) Berechne die Achsenschnittpunkte von f(x).
d) Zeichne die Graphen von f(x) und f'(x) in ein Koordinatensystem.
2. Steigung eines Funktionsgraphen
Was verstehest du unter der Steigung eines Funktionsgraphen in einem Punkt?
3. Sekantensteigung
Beschreibe anschaulich (Skizze) und mit Worten, wie man bei einem Graphen von der Sekantensteigung zur Tangentensteigung gelangt.
4.
Welche Bedeutung hat die erste Ableitung einer Funktion an der Stelle x0?
5.
Warum nennt man die Ableitungsfunktion auch Steigungsfunktion?
6. Leite folgende Funktionen 3 mal ab.
a)
![]()
b)
![]()
c)
![]()
d)
![]()
e)
![]()
f)
![]()
g)
![]()
h)
![]()
i)
![]()
j)
![]()
7. Gegeben ist die Funktion f(x).
Die Gleichungen für Tangente und Normale sollen für den Punkt P ( 2 | f(2) ) berechnet werden.
![]()
8.
Skizziereunterhalb des Funktionsgraphen den Graphen der Ableitungsfunktion und markiere in beiden Graphen die charakteristischen Punkte.
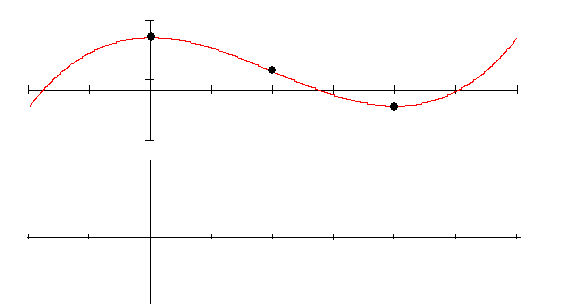
Dazu findest du hier die ausführlichen Lösungen.
Die Theorie findest du hier: Von der Sekantensteigung zur Tangentensteigung.
Hier eine Übersicht über alle Beiträge zur Differentialrechnung. Dort sind auch Links zu weiteren Aufgaben und Theorieteilen.

