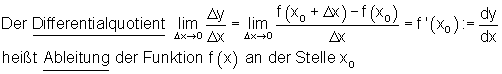Von der Sekantensteigung zur Tangentensteigung
Im letzten Beitrag hatte ich anhand praktischer Beispiele gezeigt, was Steigung und Tangente sind und damit in die Differentialrechnung eingeführt. Diesmal erkläre ich, was Sekantensteigung und Tangentensteigung sind. Außerdem geht es um die des Ableitung des Differentialquotient.
- Wofür braucht man das?
- Beispiel: Steigung einer Funktion
- Die Steigung ungefähr ermitteln
- Definition Differenzenquotient und Differentialquotient
- Bildung der Ableitung einer Funktion an der Stelle x0 und der Ableitungsfunktion
- Definition Ableitungsfunktion und Steigungsfunktion
- Beispiele zur Berechnung der Ableitung
- Potenzregel,Konstantenregel, Summenregel
- Steigungen auf einer Straße und in der Mathematik
- Funktion und Ableitungsfunktion in einem Koordinatensystem
Hier werde ich zuerst anhand eines Beispiels zeigen, dass viele Funktionen keine konstante Steigung haben. Danach erkläre ich die Begriffe Differenzenquotient und Differentialquotient und wie man die Ableitung einer Funktion an der Stelle x0 bildet. Hierzu stelle ich mehrere Beispiele vor. Dann wiederhole ich die Potenzregel, die Konstantenregel und die Summenregel. Zum Beispiel kann man die Steigungen auf einer Straße berechnen. Zuletzt stelle ich die Funktion und Ableitungsfunktion in einem Koordinatensystem vor.
Wofür braucht man die Ableitung des Differentialquotient?
In vielen Fachdisziplinen ist es notwendig, das Änderungsverhalten (Steigungsverhalten) von Abläufen (Funktionen) zu untersuchen.
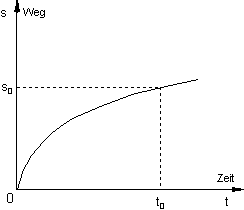
Zum Beispiel ist die Momentangeschwindigkeit v(t0) in einem Weg-Zeit-Diagramm gleich der Steigung der Funktion in dem betrachteten Augenblick.
Dieses Steigungsproblem lässt sich mit Hilfe der Differentialrechnung lösen.
Mit anderen Worten: Die Bestimmung der Steigung einer Funktion an einer vorgegebenen Stelle x0 nennt man differenzieren.
Beispiel: Steigung einer Funktion
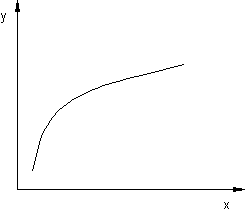
Gegen ist die Funktion y = f(x) und der dazugehörende Graph.
Betrachtet man das Steigungsverhalten der Funktion, so stellt man fest, dass die Steigung der Funktion in fast allen Punkten verschieden ist.



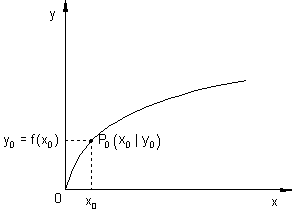
Die Steigung ungefähr ermitteln
![]()
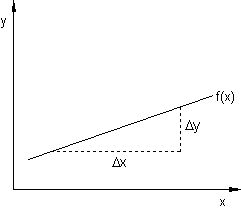
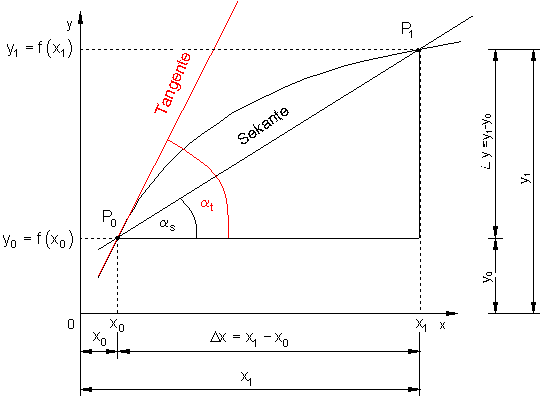
Die Gerade, die die beiden Punkte verbindet, die Sekante, weist eine Steigung auf, die der „mittleren Steigung“ der Funktion zwischen den Punkten P1 und P0 entspricht.
Diese wird über das Steigungsdreieck bestimmt.
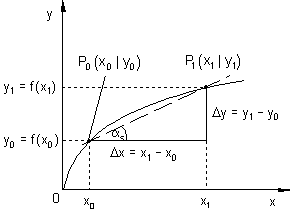
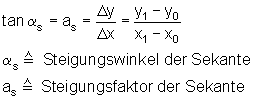
Legt man den Punkt P1 näher an P0, so entspricht die Steigung der neuen Sekante schon eher der Steigung der Funktion im Punkt P0, die ermittelt werden soll. Führt man dieses Verfahren konsequent fort, und nähert den Punkt P1 immer mehr dem Punkt P0 an, so entsteht als Grenzlage eine Gerade, die den Funktionsgraphen nur noch im Punkt P0 berührt, die Tangente an den Funktionsgraphen im Punkt P0.
Die Steigung der Tangente entspricht dann genau der Steigung des Funktionsgraphen im Punkt P0.
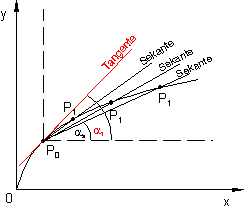
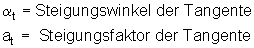
Dieses Verfahren kann man mathematisch auch durch einen Grenzwertbildung ausdrücken.
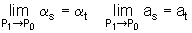
Dazu kannst du dir das 📽️ Video Sekante und Tangente ansehen.
Differenzenquotient und Ableitung des Differentialquotient

Definition Differentialquotient:
Definition Ableitung:
Die erste Ableitung einer Funktion an der Stelle x0 gibt die Steigung der Tangente an, die den Funktionsgraphen im Punkt P0 (x0 | y0) berührt und ist damit zugleich die Steigung des Funktionsgraphen im Punkt P0 (x0 | y0).
Man sagt auch Steigung der Funktion.
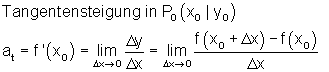
Dazu kannst du dir das 📽️ Video Differentialquotient-Differenzenquotient Unterschied ansehen.
Bildung der Ableitung einer Funktion an der Stelle x0 und der Ableitungsfunktion
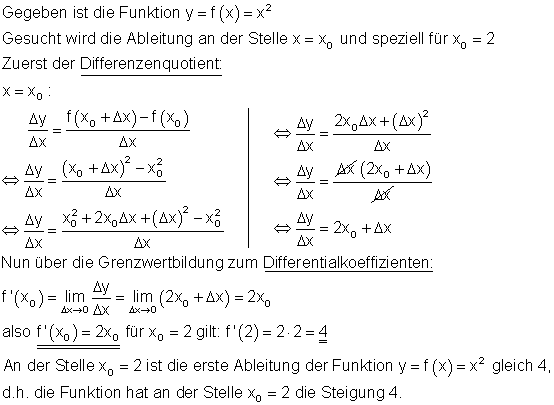
Das Ergebnis kann am Graphen der Funktion überprüft werden, in dem man im Punkt
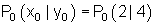
die Tangente anlegt und über ein Steigungsdreieck die Steigung ermittelt.
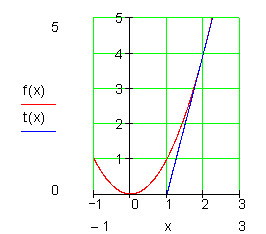

Definition Ableitungsfunktion
Wird eine Funktion abgeleitet, so entsteht wieder eine Funktion.
Diese wird Ableitungsfunktion genannt.
Definition Steigungsfunktion
Die Funktionswerte der Ableitungsfunktion stellen die Steigungen der Stammfunktion in jedem Punkt da, deshalb nennt man sie auch Steigungsfunktion.
Beispiele zur Berechnung der Ableitung eines Differentialquotient
a) Beispiel:

b) Beispiel:
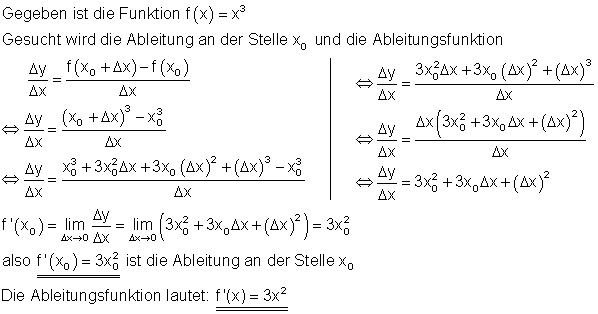
c) Beispiel:
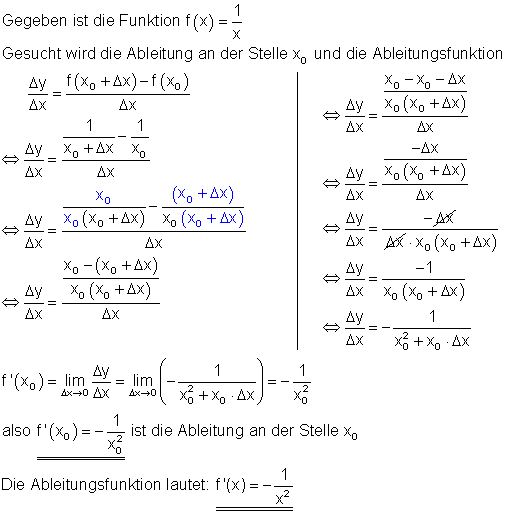
d) Beispiel:
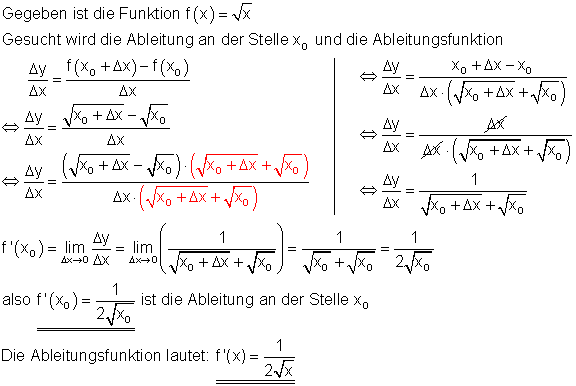
Rechnerisch wurde bisher folgendes ermittelt:

Vergleicht man diese fünf Ableitungen miteinander, so ist zu vermuten, dass folgendes Bildungsgesetz gilt:
Potenzregel (ohne Beweis)
1.) Alten Exponenten als Faktor vor die Variable x setzen.
2.) Neuer Exponent ist alter Exponent vermindert um eins.
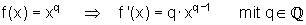
Beispiel:
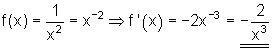
Konstantenregel
Eine Funktion ist zusammengesetzt aus einer elementaren Funktion multipliziert mit einer Konstanten.
Dann ist die Ableitung dieser Funktion gleich der Ableitung der Elementarfunktion multipliziert mit der Konstanten.
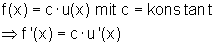
Beweis:
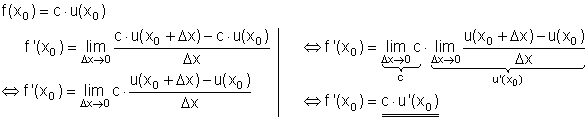
Beispiel:
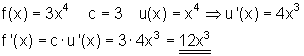
Ableitungen von Funktionen der Art f(x) = u(x) + v(x)
Summenregel
Eine Funktion ist zusammengesetzt aus der Summe zweier Funktionen.
Dann ist die Ableitung der Funktion gleich der Summe der Ableitungen der einzelnen Funktionen
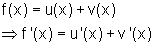
Beweis:
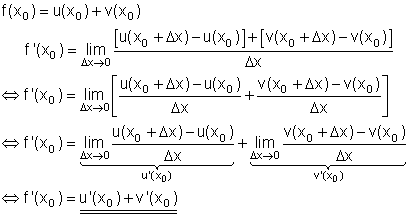
Beispiel:
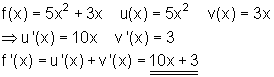
Dazu kannst du dir das 📽️Video Differentiationsregeln: Potenzregel, Konstantenregel, Summenregel ansehen.
Steigungen auf einer Straße
Stellen wir uns einen Funktionsgraphen zum Beispiel als Straße vor, die in einer Landschaft auf- und abführt, so lässt sich schön illustrieren, wie Eigenschaften eines Graphen mit der Ableitung zusammenhängen:
a) Landschaft
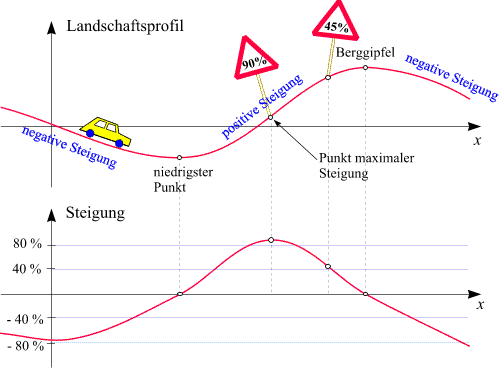
Unterhalb des Straßenverlaufs ist, in einem eigenen Diagramm, die Steigung der Straße in jedem Punkt dargestellt, dadurch ergibt sich eine zweite Kurve.
Schau dir die Diagramme genau an und versuche dann, die Details des zweiten aus den Eigenschaften des ersten zu verstehen.
Wo die Straße ihren niedrigsten Punkt hat, hat die Steigung den Wert 0%, das heißt „für einen Augenblick“ ist das Auto, wenn es diesen Punkt passiert, in horizontaler Stellung, und das gleiche gilt für den Berggipfel, über den die Straße führt.
Diese beiden Punkte sind genau jene, in denen Bereiche negativer und positiver Steigung aneinander grenzen.
Irgendwo dazwischen gibt es jedoch einen Punkt, in dem die Steigung der Straße maximal ist. (in diesem Beispiel 90%).
Dementsprechend hat die zweite Kurve dort einen „Gipfel“ – es ist aber kein Gipfel in der Landschaft, sondern anders ausgedrückt, ein „Steigungs-Gipfel“.
Nun sieh dir dieselben Kurven wie oben an, nur mit den in der Mathematik üblichen Bezeichnungen:
b) Mathematik Ableitung des Differentialquotient
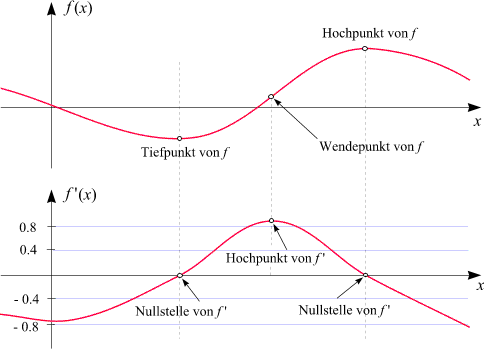
Die erste Kurve ist dabei der Graph der Funktion f(x), die zweite Kurve ist der Graph der Ableitungsfunktion f'(x).
Schau dir dann auch diese beiden Diagramme genau an und versuche nachzuvollziehen, wie ihre Details miteinander zusammenhängen.
Zwei besondere Punkte des Graphen von f(x) fallen ins Auge:
An einem ist f(x) minimal (ein Tiefpunkt), am anderen ist f(x) maximal (ein Hochpunkt).
Mit anderen Worten: An den entsprechenden Punkten besitzt f(x) Nullstellen.
Jener Punkt, in dem der Graph von f(x) am steilsten ist, heißt Wendepunkt.
Da dort die Ableitung von f(x) maximal ist (in diesem Beispiel 0,9), entspricht er einem Hochpunkt von f'(x).
Mit freiem Auge ist seine Lage aus der unteren Kurve besser zu bestimmen als aus der oberen.
Aus diesem Beispiel können wir bereits erahnen:
Ist eine Funktion f(x) gegeben, so ist in deren Ableitungsfunktion wertvolle Information über f(x) enthalten.
Sie gibt uns Auskunft über Maxima und Minima (die gemeinsam als „Extrema“ bezeichnet werden), sowie darüber, wo der Graph am steilsten ist.
Funktion und Ableitungsfunktion in einem Koordinatensystem
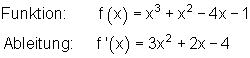
Die Ableitung einer Funktion ist wieder eine Funktion.
Wir nennen sie die Ableitungsfunktion oder auch Steigungsfunktion.
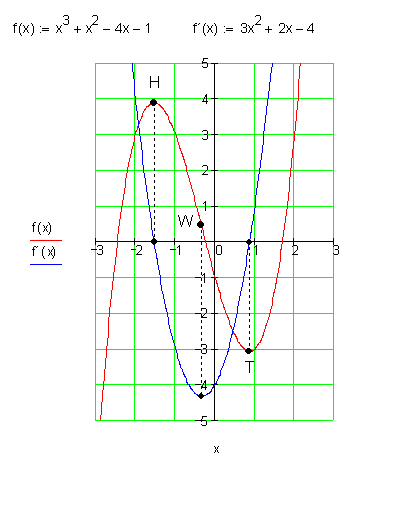
Die Graphen beider Funktionen wurden in ein Koordinatensystem gezeichnet.
Dort, wo f(x) einen Hochpunkt (H), bzw. einen Tiefpunkt (T) hat, schneidet der Graph der Ableitungsfunktion die x-Achse, hat also den Funktionswert Null.
Das leuchtet ein, denn in H und T hat f(x) waagerechte Tangenten, was bedeutet, dass in diesen Punkten die Steigung von f(x) Null ist.
Die Ableitungsfunktion f'(x) hat dort ein Minimum, wo die Steigung von f(x) betrachtet zwischen H und T betragsmäßig am größten ist.
Dazu findest du hier Aufgaben zur Differentialrechnung II.
Und Aufgaben zur Differentialrechnung VI.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung, dort auch Links zu weiteren Aufgaben.