Hier findest du die Lösungen der Aufgaben zur Differentialrechnung IV mit komplettem Lösungsweg. Ähnlich wie in den Aufgaben zur Differentialrechnung I, II und III muss man hier Funktionen ableiten und die Steigung berechnen.
1. a) Chemische Reaktionen
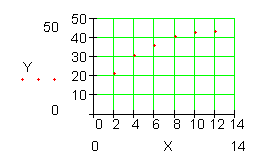
b) Die Wasserstoffproduktion pro Zeiteinheit wird immer geringer.
c)
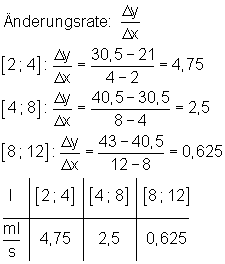
2. Berechne die Änderungsrate
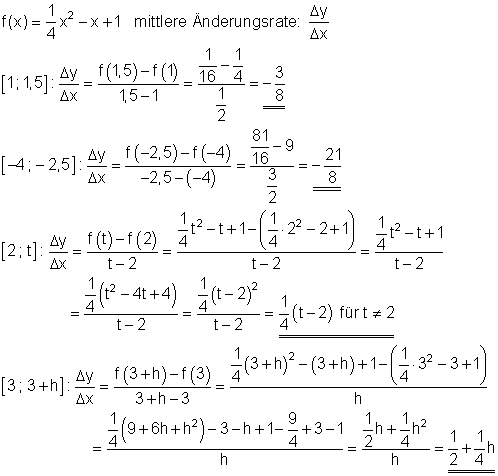
3. Gegeben ist die Funktion f(x) = \frac{3}{4}x^2 - 3x .
a)
f(x) = \frac{3}{4}x^2 - 3x die mittlere Änderungsrate in [2 ; 5] ist \dfrac{\Delta y}{\Delta x} = \frac{f(5) - f(2)}{5 - 2}
f(5) = \frac{3}{4} \cdot 25 - 3 \cdot 5 = 3,75 f(2) = \frac{3}{4} \cdot 4 - 3 \cdot 2 = -3 \Delta x = 5 - 2 = 3 \\
\Rightarrow \dfrac{\Delta y}{\Delta x} = \frac{3,75 - (-3)}{3} = \frac{6,75}{3} = \underline{\underline{ 2,25}}
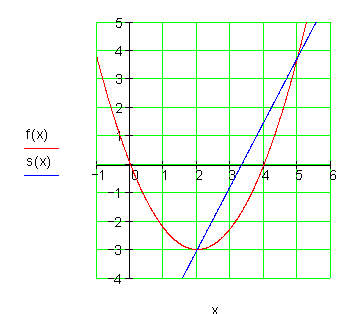
3b) Die Gleichung der Sekante s(x) durch die Punkte P und Q ist genauso zu bestimmen wie die Gleichung einer Geraden durch zwei Punkte.
P(2 | f(2)) \Rightarrow aus Aufgabenteil a) P(2 | - 3)
Q(5 | f(5)) \Rightarrow aus Aufgabenteil a) Q(5 | 3,57) \\
s(x) = a_1 \cdot x + a_0 mit a_1 = \dfrac{\Delta y}{\Delta x} = \dfrac{(f(5) - f(2)}{5 - 2} = 2,25 siehe Aufgabenteil a) \\
\Rightarrow s(x) = 2,25x + a_0 \\
P(2 | -3) : s(2) = - 3 \Leftrightarrow 2,25 \cdot 2 + a_0 = -3 \Leftrightarrow a_0 = -7,5 \\
\Rightarrow s(x) = 2,25 x - 7,5 ist die Sekantengleichung.
3c)
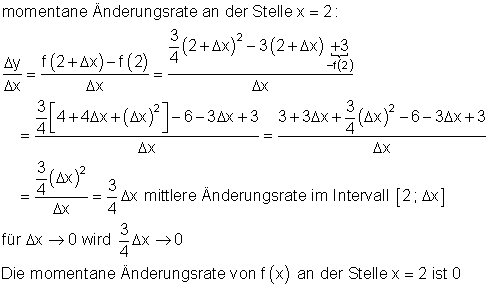
3d)
4. Freier Fall
Die momentane Geschwindigkeit ist gleichbedeutend mit der momentanen Änderungsrate.
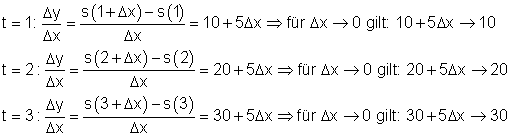
5. Ein Pudding kühlt nach seiner Zubereitung ab.
a) Die anfängliche Temperatur lässt sich aus dem Graphen zu 90 0C ablesen.
b) Die Funktionswerte streben asymptotisch gegen den Wert 20 0C.
c) Die Abkühlungsgeschwindigkeit ist zu Beginn des Vorgangs am größten.
d) Das negative Vorzeichen bedeutet, dass die Änderungsrate negativ ist,die Temperatur des Puddings nimmt ab.

Hier findest du die Aufgaben
und hier die Theorie: Steigung und Tangente.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung, darin auch Links zu weiteren Aufgaben.

