In diesem Beitrag zeige ich zuerst anhand des Beispiels, wie die Höhe eines Flugzeuges schwankt. Dadurch wird klar, wofür man die Differentialrechnung braucht. Danach erkläre ich, wie man die Steigung eines Funktionsgraphen in einem Punkt berechnet. Zuletzt stelle ich ein mathematisches Verfahren zur Berechnung der momentanen Änderungsrate vor.
- Beispiel
- Definition Steigung eines Funktionsgraphen
- Berechnung der Steigung eines Funktionsgraphen in einem Punkt
- Mathematisches Verfahren zur Berechnung der momentanen Änderungsrate
1. Beispiel: Steigung eines Funktionsgraphen in einem Punkt
Nachdem wir uns intensiv mit ganzrationalen Funktionen beschäftigt haben, nähern wir uns nun der Differentialrechnung. Mathematikleher werden oft von ihren Schülern gefragt: Wofür brauchen wir das alles? Hier haben wir eine Antwort: Funktionen verlaufen in der Praxis nicht immer gleichmäßig, sondern schwanken. Dies führt uns zu einer einfachen Erklärung der Differentialrechnung: Sie hilft uns, diese Schwankungen zu berechnen. Dies werde ich hier anhand einiger Beispiele aus der Praxis zeigen.
In Segelflugzeugen sind häufig Flugschreiber eingebaut, die die Flughöhe in Abhängigkeit von der Flugzeit automatisch aufzeichnen.
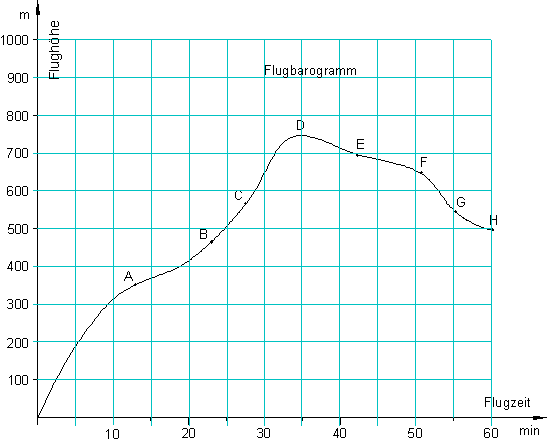
Aufgabe:
Vergleiche die Steigung des Graphen im Punkt A mit der des Graphen im Punkt B. Vergleiche entsprechend die des Graphen in den Punkten E und G.
Erkläre dann, warum man von der Steigung in einem Punkt sprechen muss.
Versuche anschließend ein Maß für die Steigung des Graphen in einem Punkt zu definieren und bestimme aus der Zeichnung die Steigung im Punkt A und im Punkt B.
Bearbeitung:
Die Steigung des Graphen im Punkt B ist größer als die des Graphen im Punkt A. Wohingegen die in den Punkten E und G negativ sind. Dabei ist die Steigung im Punkt E betragsmäßig kleiner als im Punkt G.
Aber die Steigung eines Graphen ist nicht überall gleich. Deshalb muss der Punkt angegeben werden, in dem sie betrachtet wird. Lediglich die Steigung einer Geraden ist überall gleich. Daher kann man von der Steigung einer Geraden sprechen.
An dieser Stelle möchte ich kurz wiederholen: Eine Gerade, die einen Graphen in genau einem Punkt berührt, nennt man Tangente. Siehe hier.
Deshalb scheint folgende Definition vernünftig zu sein:
2. Definition: Steigung eines Funktionsgraphen
Die Steigung eines Funktionsgraphen in einem Punkt P ist gleich der Steigung der Tangente an den Graphen in diesem Punkt.

Hierbei ist eine Tangente zunächst anschaulich als Gerade definiert, die sich dem Graphen in einer Umgebung des Berührungspunktes möglichst gut anschmiegt.
Durch diese Definition ist die Steigung eines Graphen in einem Punkt zurückgeführt auf die einer Geraden.
Zur Bestimmung der Steigung des Graphen in den Punkten A und B zeichnen wir jeweils eine Gerade (Tangente) durch diese Punkte, die sich dem Graphen möglichst gut anpasst.
Mit Hilfe eines Steigungsdreiecks lässt sich die Steigung grob bestimmen:
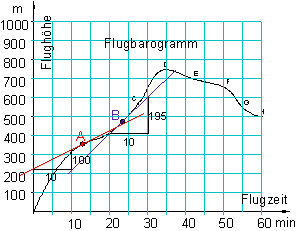
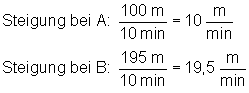
Für unser Beispiel hat die Steigung in einem bestimmten Punkt die Bedeutung der momentanen Höhenänderungsrate oder der Steiggeschwindigkeit.
Punkt A: Flugzeit ca. 12,5 min, Steiggeschwindigkeit ca. 10 m / min.
Punkt B: Flugzeit ca. 23,0 min, Steiggeschwindigkeit ca. 19,5 m / min.
Die Tangente ist bisher nur anschaulich als eine Gerade definiert, die sich dem Graphen in einer Umgebung des Berührungspunktes besonders gut anschmiegt. Deswegen konnte die Steigung des Graphen in den Punkten A und B auch nur näherungsweise bestimmt werden. Aber das ist für die Praxis unbefriedigend.
3. Berechnung der Steigung eines Funktionsgraphen in einem Punkt
Bekanntlich erhöht ein Zug, der aus einem Bahnhof herausfährt nur langsam seine Geschwindigkeit. Der zurückgelegte Weg (Entfernung vom Bahnhof) wird dabei immer größer. Die Entfernung vom Bahnhof hängt also von der Zeit ab.
Dieser Vorgang kann durch folgende Funktionsgleichung beschrieben werden:
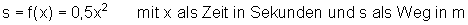
Der Funktionsgraph: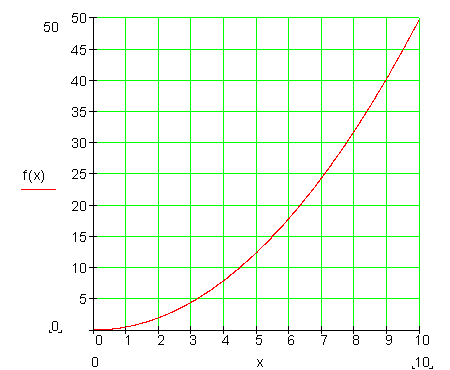
Es soll nun die mittlere Änderungsrate (mittlere Steigung) zwischen der 3. und der 7. Sekunde berechnet werden. Dazu zeichnen wir die entsprechende Sekante ein und berechnen deren Steigung.
Des weiteren soll die Änderungsrate zwischen der 3. und der 4. Sekunde berechnet werden.
Wie groß ist die Änderungsrate in der 3. Sekunde?
Führe deine Berechnung der mittleren Steigung so aus, dass der Abstand zwischen den Punkten P1 und P0 immer kleiner wird, indem sie den Punkt P1 auf den Punkt P0 zu bewegen.
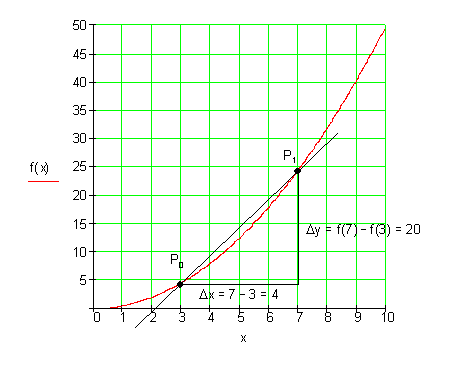
\Delta ist das mathematische Zeichen für eine Differenz.

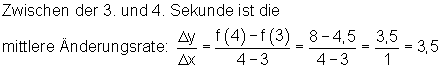

Die Rechnung zeigt, wenn wir den Punkt P1 näher an den Punkt P0 wandern lassen, nähert sich der Wert der Änderungsrate (Steigung) immer mehr dem Wert 3.
Wir erhalten so einen Wert, der der momentanen Änderungsrate immer näher kommt.
Betrachten wir die physikalischen Einheiten in unserem Beispiel, so gilt für die Änderungsrate m/s.
Das ist die Einheit für die Geschwindigkeit.
Das bedeutet, die Änderungsrate in einem Weg-Zeit-Diagramm entspricht der Geschwindigkeit.
4. Mathematisches Verfahren zur Berechnung der momentanen Änderungsrate

Im nächsten Beitrag werde ich nun anhand von Beispielen aus der Praxis erklären, was der Differentialquotient ist und wie man ihn ableitet.
Dazu findest du hier Aufgaben zur Differentialrechnung I.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.


