In diesem Beitrag findest du eine Übersicht aller Formeln zu ganzrationalen Funktionen. Dabei berücksichtige ich Symmetrien, Achsenschnittpunkte, Nullstellenberechnung, interaktive Hilfsmittel und viele Beispiele. Dazu führe ich Definitionen, Formeln und Vorgehensweisen an. Außerdem gebe ich viele Beispiele.
- Definition ganzrationale Funktion
- Verlauf des Graphen einer ganzrationale Funktion
- Symmetrien
- Achsenschnittpunkte
- Verfahren zur Nullstellenberechnung
Faktorisierungsverfahren - Substitutionsverfahren
- Polynomdivision
- Graphen zeichnen
- Wertetabelle
- Berechnung der Nullstellen für den Graphen
- Funktionsgleichung aufstellen
- Interaktive Hilfsmittel für Funktionen
- Link zu weiteren Beiträgen und Aufgaben
Definition ganzrationale Funktion
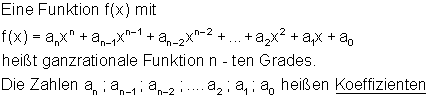
Beispiele ganzrationale Funktionen:
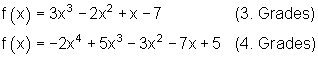
Verlauf des Graphen einer ganzrationalen Funktion
Der Verlauf des Graphen einer ganzrationalen Funktion wird durch den Summanden mit der höchsten Potenz bestimmt.
| n gerade | n ungerade | |
| an>0 | Verlauf von II nach I | Verlauf von III nach I |
| an<0 | Verlauf von III nach IV | Verlauf von II nach IV |
Beispiele:
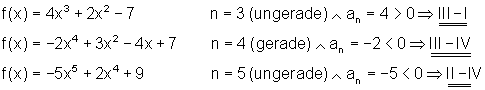
Symmetrien einer ganzrationalen Funktion
Der Graph einer ganzrationalen Funktion ist genau dann achsensymmetrisch, wenn die Funktionsgleichung nur aus geraden Exponenten besteht. Oder es gilt folgendes:
Der Graph einer ganzrationalen Funktion ist genau dann punktsymmetrisch, wenn die Funktionsgleichung nur aus ungeraden Exponenten besteht. Oder es gilt folgendes:
Bemerkung:
Unter Achsensymmetrie versteht man die Symmetrie zur y-Achse. Punktsymmetrie ist dagegen die Symmetrie zum Koordinatenursprung.
Achsenschnittpunkte einer ganzrationalen Funktion
Beispiel:
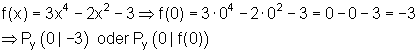
Die y-Koordinate von Py ist immer identisch mit dem Koeffizienten a0.
Sie lässt sich stets aus der Funktionsgleichung ablesen.
Wie viele Nullstellen hat eine ganzrationale Funktion?
Eine ganzrationale Funktion n ten Grades hat höchstens n Nullstellen. Ist der Grad n ungerade, so hat sie mindestens eine Nullstelle.
Verfahren zur Nullstellenberechnung einer ganzrationalen Funktion
Faktorisierungsverfahren:
Substitutionsverfahren
Polynomdivision
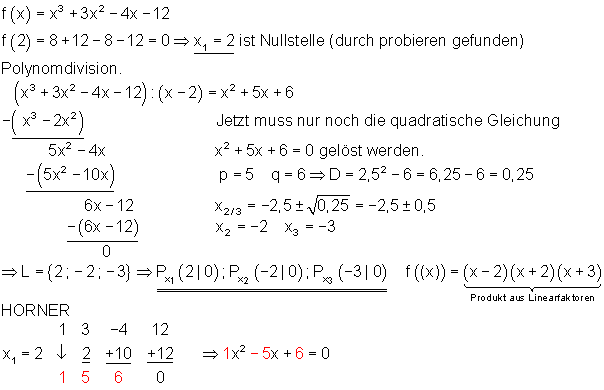
Graphen zeichnen
Wertetabelle:
Eine Möglichkeit die Wertetabelle zu erhalten besteht darin, alle benötigten Funktionswerte mit dem Taschenrechner auszurechnen. Aber oft ist das Hornerschema einfacher.
Nachfolgend ist das Prinzip des Hornerschemas grafisch dargestellt.
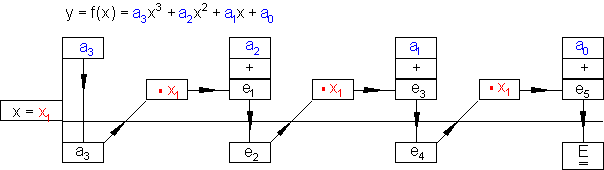
Beispiel:
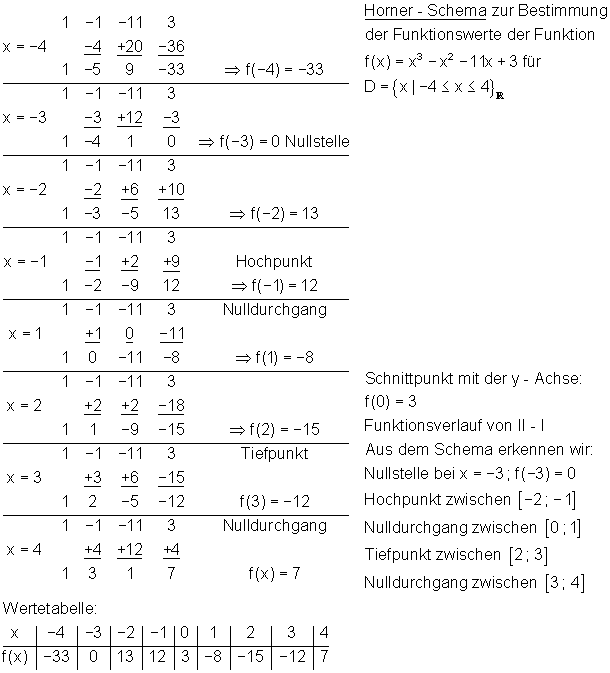
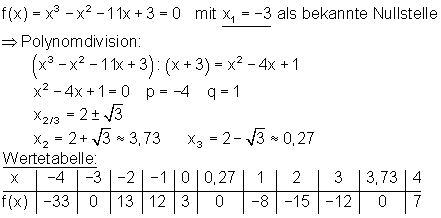
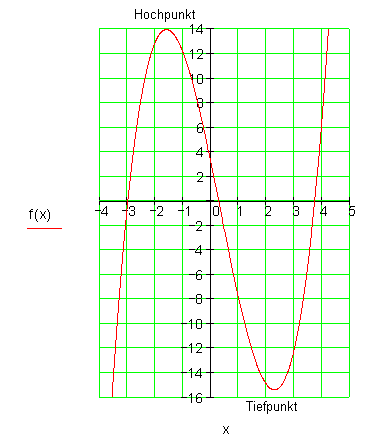
Aber wir können noch nicht genau den Hoch- und Tiefpunkt des Graphen bestimmen. Dazu benötigen wir die Differentialrechnung in einem späteren Kapitel.
Funktionsgleichung aufstellen
Beispiel für eine Ganzrationale Funktion 3. Grades.
Wir haben folgende Koordinaten von 4 Punkten, die auf dem Funktionsgraphen liegen:
Zunächst stellen wir das Gleichungssystem für die gegebenen Punkte auf.
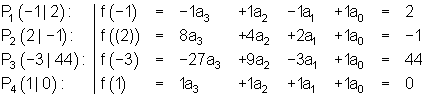
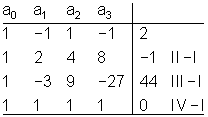
Interaktive Hilfsmittel für Funktionen
Interaktiv: Parabel durch drei Punkte: Wenn du drei Punkte eingibst, berechnet und zeichnet das Programm die Parabel.
Interaktiv: Graphen zeichnen: Gib Koeffizienten und die Potenz für x ein, dann zeichnet das Javascript den Graphen.
Außerdem Interaktiv: Ganzrationale Funktion 3. Grades durch 4 Punkte: Gib 4 beliebige Punkte ein, danach berechnet das Javascript die Funktionsgleichung und zeichnet den Graphen.
Interaktiv: Ganzrationale Funktion 4. Grades durch 5 Punkte: Gib 5 beliebige Punkte ein, danach berechnet das Javascript die Funktionsgleichung und zeichnet den Graphen.
Hier findest du eine Übersicht über alle Beiträge zum Thema weitere ganzrationale Funktionen.
