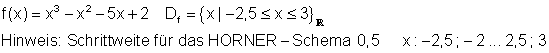Aufgaben Ganzrationale Funktionen I zur Vorbereitung einer Klassenarbeit Nullstellen

Bei diesen Aufgaben zu ganzrationalen Funktionen I geht es unter anderem um Nullstellen und Symmetrie.

1. Bedeutung?

Was bedeutet:   a_nx^n + a_{n-1}x^{n-1} + ... + a_2x^2 + a_1x + a_0 ?

2. Symmetrie

Was weißt du über die Symmetrie ganzrationaler Funktionen ?

3. Symmetrieeigenschaft

Mache eine Aussage über die Symmetrieeigenschaft folgender Funktionen und begründe deine Aussage.
a)

b)

c)

d)

4. Verlauf

Wodurch wird der Verlauf einer ganzrationalen Funktion bestimmt?

5. Wie verlaufen folgende Funktionsgraphen?

a)

b)

c)

d)

6.  Nullstellen

Was weißt du über die Anzahl der Nullstellen ganzrationaler Funktionen?

7. Welcher Art sind die Nullstellen

Berechne die Nullstellen folgender Funktionen und stelle die Funktionsgleichung als Produkt von Linearfaktoren dar. Welcher Art sind die Nullstellen (einfach, doppelt oder dreifach)?
a)

b)

8. Verlauf des Graphen

Berechne die Nullstellen folgender Funktionen. Mache eine Aussage über den Verlauf des Graphen. Wohin streben die Funktionswerte für große, bzw. kleine x- Werte?
a)

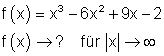
b)

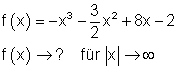
9. Hornerschema

Berechne für f(x) nach dem Hornerschema die Wertetabelle, berechne die Nullstellen und zeichne den Graphen so genau wie möglich.

Dazu kannst du dir das 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.

10. Ausführliche Aufgabe

Der Graph einer ganzrationalen Funktion 3. Grades geht durch die Punkte P₁(1|1); P₂(2|0); P3(-2|4); P4(3|9);
a) Bestimme die Funktionsgleichung.
Dazu kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.
b) Bestimme die Achsenschnittpunkte.
c) Ermittele mit dem Hornerschema die Funktionswerte für  x = -1,5; x = – 0,5; x = 0,5; x = 1,5; x = 2,5
d) Trage alle bekannten Werte in eine Wertetabelle ein.
e) Zeichne den Graphen 1 cm = 1 Einheit.

f) Mache eine Aussage über den Verlauf des Graphen für große und kleine x-Werte.
g) Mache eine Symmetriebetrachtung. Begründe dein Ergebnis.

Dazu findest du hier die ausführlichen Lösungen.

Und hier die dazugehörige Theorie: Zusammenfassung ganzrationale Funktionen.

Hier eine Übersicht über weitere ganzrationale Funktionen, darin Links zu weiteren Aufgaben.