Hier findest du die Lösungen der Aufgaben zu ganzrationalen Funktionen I mit Textaufgaben und Anwendungsaufgaben aus Technik und Wirtschaft mit komplettem Lösungsweg.
1. Herstellung einer Ware
Als erstes stellen wir das Gleichungssystem auf:
f(x) = a_3x^3 + a_2x^2 + a_1x + a_0
P_1(5 | 915): f(5) = 125a_3 + 25a_2 + 5a_1 + a_0 = 915 \\
P_2 ( 10 | 1035) : f(10) = 1000a_3 + 100a_2 + 10a_1 + a_0 = 1035 \\
P_3( 20 | 1140) : f(20) = 8000a_3 + 400a_2 + 20a_1 + a_0 = 1140 \\
P_4 ( 35 | 1185): f(35) = 42875a_3 + 1225a_2 + 35a_1 + a_0 = 1185
Danach berechnen wir mit dem Gauß-Algorithmus:
Dazu kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.

Die Koeffizienten und die Funktionsgleichung lauten deshalb:
11250a_3 = 225 \Leftrightarrow a_3 = \frac{225}{11250} = 0,02
150a_2 + 5250a_3 = -135 \\ \Leftrightarrow a_2 = \frac{-135 - 5250 \cdot 0,02}{150} = -1,6
5a_1 + 75a_2 + 875a_3 = 120 \\ \Leftrightarrow a_1 = \frac{120 - 75 \cdot (-1,6) - 875 \cdot 0,02}{5} = 44,5
a_0 + 5a_1 + 25a_2 + 125a_3 = 915 \\
\Leftrightarrow a_0 = 915 - 5 \cdot 44,5 - 25 \cdot (-1,6) - 125 \cdot 0,02 = 730
Die Funktionsgleichenung lautet daher:
\underline{\underline{ K(x) = 0,02x^3 - 1,6x^2 + 44,5x + 730}}
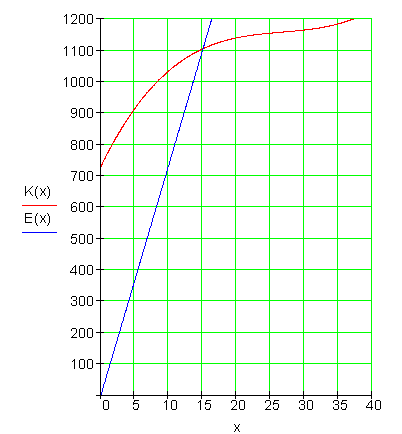
Die Kosten für die Herstellung von x = 15 Stück sind wie folgt:
K(15) = 0,02 \cdot 15^3 - 1,6 \cdot 15^2 + 44,5 \cdot 15 + 730 = 1105
Die Erlösfunktion sieht dann so aus:
E(x) = p \cdot x mit p als Verkaufspreis pro Stück.
Der Mindestpreis pro Stück ist also:
p = \frac{1105}{15} = 73 \frac{2}{3} \Rightarrow E(x) = 73 \frac {2}{3}x
Der Verkaufspreis pro Stück sollte demnach mindestens
\underline{\underline{73 \frac {2}{3}}} € betragen.
2. Flugkurve
2. a)
Die maximale Höhe des Balls lässt sich aus der Grafik zu 3 m ablesen. Die Entfernung vom Abschusspunkt beträgt etwa 12 m. Eine exakte Berechnung ist erst mit Hilfe der Differentialrechnung möglich. Wir überprüfen die Abschätzung durch Rechnung. Dabei untersuchen wir die Funktionswerte in der Umgebung von x = 12.
f(11,5) = -\frac{1}{288} \cdot 11,5^3 + \frac{1}{16} \cdot 11,5^2 \approx 2,985
f(12) = -\frac{1}{288} \cdot 12^3 + \frac{1}{16} \cdot 12^2 = 3 \\
f(12,5) = -\frac{1}{288} \cdot 12,5^3 + \frac{1}{16} \cdot 12,5^2 \approx 2,894 \\
f(11,75) = -\frac{1}{288} \cdot 11,75^3 + \frac{1}{16} \cdot 11,75^2 \approx 2,996 \\
f(12,25) = -\frac{1}{288} \cdot 12,25^3 + \frac{1}{16} \cdot 12,25^2 \approx 2,996
Wir könnten nun die Intervalle immer enger machen und würden dadurch dem Wert 3 immer näher kommen.
2. b)
Gesucht ist die Flugbahnhöhe in einem Abstand von 9,15 m vom Abschusspunkt, denn dort steht die Mauer der Abwehrspieler.
f(9,15) = -\frac{1}{288} \cdot 9,15^3 + \frac{1}{16} \cdot 9,15^2 \approx 2,573
Der Ball überfliegt die Abwehrmauer ( 2,573 m > 2 m ).
2. c)
Um den Auftreffpunkt des Balles zu bestimmen, sind die Nullstellen des Funktionsgraphen zu bestimmen.
f(x) = 0 \Leftrightarrow -\frac{1}{288}x^3 + \frac{1}{16} x^2 = 0
\Leftrightarrow x^2(-\frac{1}{288}x + \frac{1}{16}) = 0 \Leftrightarrow \underline{\underline{x^3 = 18}}
Der Ball schlägt 18 m vom Abschusspunkt auf dem Boden auf.
d) Gesucht ist die Entfernung vom Abschusspunkt, in der der Ball eine Höhe von 2 m hat. Aus der Grafik lesen wir zwei Werte ab, sie liegen bei etwa 7,50 m und 16 m. Angesichts der Flugbahn des Balles untersuchen wir die Umgebung von 16 m.
f(x) = 2 \Leftrightarrow -\frac{1}{288}x^3 + \frac{1}{16} x^2 = 2
\Leftrightarrow -\frac{1}{288}x + \frac{1}{16} - 2 = 0 \\ \Leftrightarrow x^3 - 18x^2 + 576 = 0 \\
x = 16 \Rightarrow 16^3 - 18 \cdot 16^2 + 576 = 64 > 0 \\
x = 15,5 \Rightarrow 15,5^3 - 18 \cdot 15,5^2 + 576
\approx -24 < 0 \\
x = 15,75 \Rightarrow 15,75^3 - 18 \cdot 15,75^2 + 576
\approx 18 > 0 \\
x = 15,7 \Rightarrow 15,7^3 - 18 \cdot 15,7^2 + 576
\approx 19 > 0 \\
x = 15,65 \Rightarrow 15,65^3 - 18 \cdot 15,65^2 + 576
\approx 0,4 > 0
In einer Entfernung von etwa 15,65 m vom Abschusspunkt überfliegt der Ball die Torlinie in 2 m Höhe.
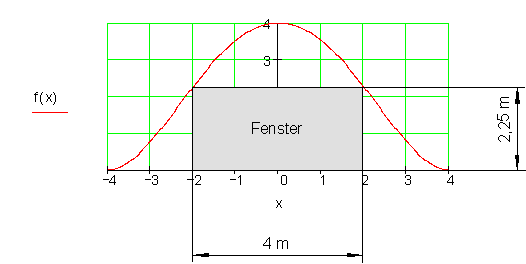
3. Giebel
3. a)
Die Randfunktion ist eine ganzrationale Funktion 4. Grades weil sie zwei doppelte Nullstellen besitzt. (x1 = -4 ; x2 = 4)
3. b)
Als erstes stellen wir den Ansatz auf:
f(x) = a_4(x + 4)^2 (x - 4)^2
P(0|4): f(0) = a_4(4)^2 (-4)^2 = 4 \\
\Leftrightarrow a_4 = \frac{4}{4^4} = \frac{1}{4^3} = \frac{1}{64} \\
\Rightarrow f(x) = \frac{1}{64} (x + 4)^2 (x - 4)^2 = \underline{\underline{ \frac{1}{64}x^4 - \frac{1}{2}x^2 + 4}}
3. c)
f(\frac{b}{2}) = 2,25 \Leftrightarrow \frac{1}{64}x^4 - \frac{1}{2}x^2 + 4 = 2,25
\Leftrightarrow \frac{1}{64}x^4 - \frac{1}{2}x^2 + 1,75 = 0 \\
\Leftrightarrow x^4 - 32x^2 + 112 = 0
Hier haben wir also eine biquadratische Gleichung. Deshalb setzen wir z ein:
x^2 = z \Rightarrow z^2 - 32z + 112 = 0 \\
\Rightarrow p = -32 ; q = 112 \Rightarrow D = 144 \\
z_1 = 16 + \sqrt 144 = 16 + 12 = 28 \\
z_2 = 16 - \sqrt 144 = 16 - 12 = 4 \\
x^2 = z \Rightarrow x_1^2 und x_2^2 \\
x_1^2 = 28 \Rightarrow |x_1| = \sqrt28 \Rightarrow x_{1-1} \approx 5,29 ; x_{1-2} \approx -5,29 \\
x_2^2 = 4 \Rightarrow |x_2| = \sqrt 4 \Rightarrow x_{2-1} = 2 ; x_{2-2} = -2 \\
\Rightarrow \frac{b}{2} = 2m \Rightarrow Das Fenster kann höchstens \underline{\underline{ 4 m}} breit sein.
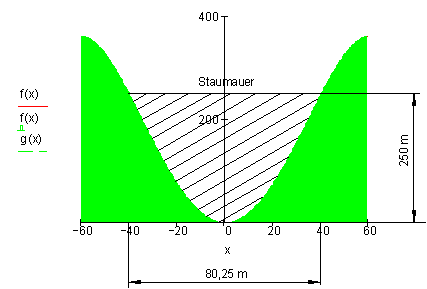
4. Gebirgstal
a)
Als erstes stellen wir den Ansatz auf:
f (x) = a_4x^4 + a_2x^2 \\
P_1(60 | 360): \quad f(60) = 12 960 000 a_4 + 3 600a_2 = 360 \\
P_2(30 | 157,5): f(30) = 810 000a_4 + 900a_2 = 157,5
| a4 | a2 | |
|---|---|---|
| 810000 | 900 | 157,5 |
| 12 960 000 | 3600 | 360 II – 16 · I |
| 810000 | 900 | 157,5 |
| 0 | -10800 | -2160 |
-10800a_2 = -2160 \Leftrightarrow a_2 = \underline{0,2} \\
810000a_4 + 900a_2 = 157,5
\Leftrightarrow a_4 = \frac{157,5 - 180}{810000} = \underline{ -\frac{1}{36000}} \\
\Rightarrow \underline{\underline{ f(x) = -\frac{1}{36000}x^4 + \frac{1}{5}x^2}}
4. b)
f(\frac{b}{2}) = 250 \Leftrightarrow -\frac{1}{36000}x^4 + \frac{1}{5}x^2 = 250
\Leftrightarrow -\frac{1}{36000}x^4 + \frac{1}{5}x^2 - 250 = 0 \\
x^4 - 72000x^2 + 9000000 = 0
Als nächstes setzen wir in z ein:
x^2 = z \Rightarrow z^2 - 7200z + 9000000 = 0
\Rightarrow p = -7200 ; q = 9000000 \Rightarrow D = 3960000 \\
z_1 = 3600 + \sqrt {3960000} \approx 5589,975 \\
z_2 = 3600 - \sqrt {3960000} \approx 1610,025 \\
x^2 = z \Rightarrow x_1^2 und x_2^2 \\
x_1^2 = 3600 + \sqrt {3960000} \Rightarrow x_{1-1/2} = \pm \sqrt {3600 + \sqrt {3960000}} \approx \pm 74,766 \\
x_2^2 = 3600 - \sqrt {3960000} \Rightarrow x_{2-1/2} = \pm \sqrt {3600 - \sqrt {3960000}} \approx \pm 40,125 \\
\frac{b}{2} \approx 40,125 m \Rightarrow Die Breite der Dammkrone beträgt \underline{\underline{80,25 Meter. }}
Dazu findest du hier die Aufgaben.
Und hier die dazugehörige Theorie: Aufstellen der Funktionsgleichung aus gegebenen Bedingungen.
und hier eine Übersicht über weitere ganzrationale Funktionen.