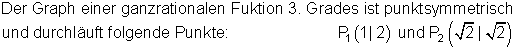In diesem Beitrag erkläre ich, wie man die Funktionsgleichung einer Parabel für ganzrationale Funktionen bis zu 4. Grades durch 5 Punkte bestimmt. Mit anderen Worten: wie man ein Polynom aus Punkten bestimmen kann.
- Wiederholung: Funktionsgleichung einer Parabel bestimmen, interaktiven Rechner dazu
- Funktionsgleichung für eine ganzrationale Funktion 3. Grades durch 4 Punkte aufstellen
- Gleichungssystems mit dem Gauß-Algorithmus lösen, Beispiele
- Trainingsaufgaben 1 dazu
- Ganzrationale Funktion 4. Grades durch 5 Punkte
- Punktsymmetrie ganzrationaler Funktionen 3. Grades
- Ganzrationale Funktion 4. Grades durch (0 | 0) und 4 Punkte
- Ganzrationale Funktion 4. Grades achsensymmetrisch durch 3 Punkte
- Trainingsaufgaben 2 dazu
1. Wiederholung:
Um die Funktionsgleichung einer Parabel zu bestimmen, sind die Koordinaten von drei Punkten nötig. Denn die brauchen wir um die Koeffizienten a2 , a1 und a0 zu bestimmen.
Siehe Parabel durch drei Punkte.
Interaktiver Rechner: Parabel 2. Grades durch drei Punkte:
Dazu stelle ich hier diesen interaktiven Rechner zur Verfügung. Wenn du die drei Punkte eingibst, berechnet und zeichnet das Programm die Parabel.
Funktionsgleichung einer ganzrationalen Funktion 3. Grades:
Tipp:
Für eine Ganzrationale Funktion n-ten Grades benötigt man also n + 1 Bedingungen und damit n + 1 Bestimmungsgleichungen.
2. Ganzrationale Funktion 3. Grades durch 4 Punkte
Zuerst stellen wir ein Gleichungssystem für die gegebenen Punkte auf:
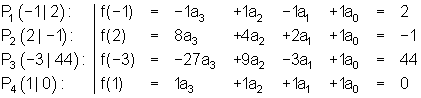
3. Gleichungssystems mit dem Gauß-Algorithmus lösen
Weil die Punkte schon tabellenartig angeordnet sind, bietet sich der Gauß-algorithmus an.
4. Trainingsaufgaben 1
Dazu findest du im Teil I dieses Beitrags Aufgaben.
Interaktiver Rechner: Ganzrationale Funktion 3. Grades durch 4 Punkte:
Gib 4 beliebige Punkte ein, danach berechnet das Javascript die Funktionsgleichung und zeichnet den Graphen.
5.) Ganzrationale Funktion 4. Grades durch 5 Punkte
Danach können wir dies mittels des Gauss-Algorithmus lösen:
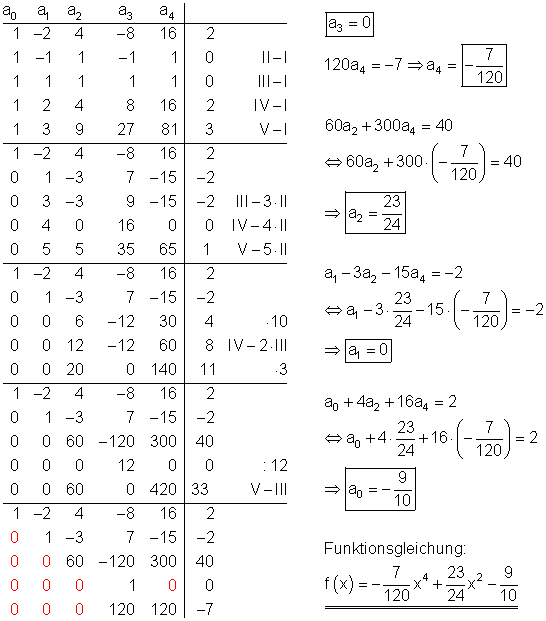
Dann ermitteln wir den Funktionsgraph über eine Wertetabelle.
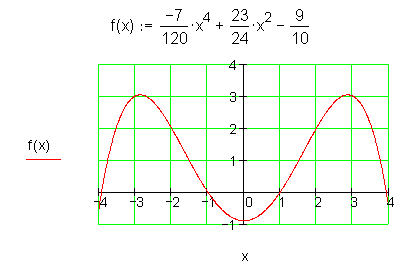
Wenn man weitere Eigenschaften des Funktionsgraphen kennt, kann man die Anzahl der Bestimmungsgleichungen reduzieren.
Interaktiv: Ganzrationale Funktion 4. Grades durch 5 Punkte
Gib 5 beliebige Punkte ein, danach berechnet das Javascript die Funktionsgleichung und zeichnet den Graphen.
6.) Ganzrationale Funktion 3. Grades punktsymmetrisch durch 2 Punkte
Wegen der Punktsymmetrie besteht die Funktionsgleichung nur aus Summanden mit ungeraden Exponenten.
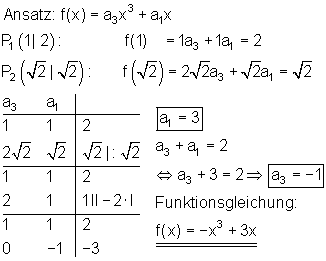
7.) Ganzrationale Funktion 4. Grades durch (0 | 0) und 4 Punkte
Die Koordinaten von 4 Punkten sind gegeben. Der 5. Punkt ist der Ursprung. Dadurch entstehen 4 Bestimmungsgleichungen.
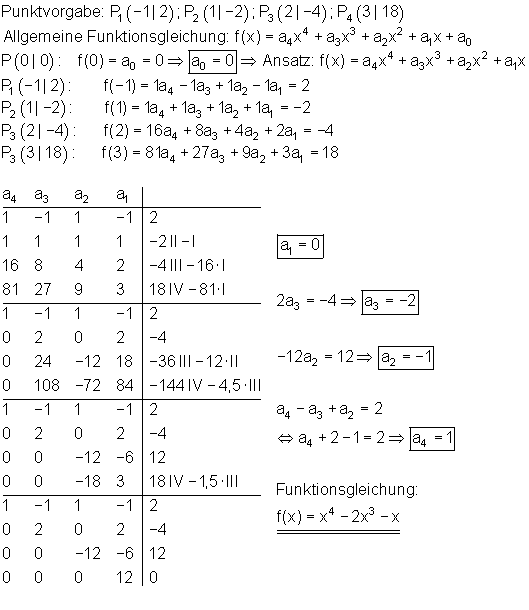
8.) Ganzrationale Funktion 4. Grades achsensymmetrisch durch 3 Punkte
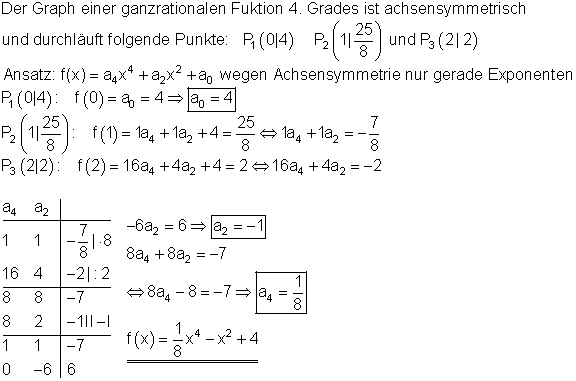
Alle Nullstellen und ein Punkt sind vorgegeben
Z. B. Ganzrationale Funktion 3. Grades.
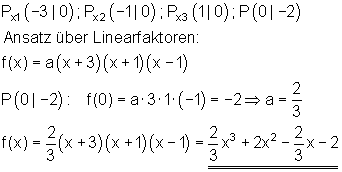
Z. B. Ganzrationale Funktion 4. Grades.
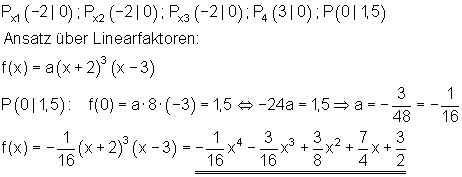
Hier weitere Text- und Anwendungsaufgaben aus Technik und Wirtschaft zu ganzrationalen Funktionen I.
Außerdem findest du eine Übersicht über alle Beiträge zum Thema weitere ganzrationale Funktionen. Darin auch Links zu weiteren Aufgaben.
