Gauß Algorithmus

Hier erkläre ich den die Regeln des Gauß Algorithmus für Anfänger. Dazu gebe ich viele Beispiele. Mit Klick auf eine Zeile in der Inhaltsübersicht, gelangst du sofort zu der Stelle, die dich interessiert:

Gauss-Algorithmus leicht verständlich erklärt
Regeln des Gauß Algorithmus
Tipps für blutige Anfänger des Gauss Algorithmus
Ausführlicher, anschauliche Beispiele
Links zu Aufgaben

Gauss-Algorithmus leicht verständlich erklärt

Wir haben mehrere Methoden kennengelernt, um lineare Gleichungssysteme mit 2 Variablen zu lösen. Dazu gehört auch das Verfahren, die beiden Gleichungen zu addieren. Das kannst du dir auch in diesem 📽️Video Zwei lineare Gleichungen addieren lösen noch einmal ansehen.

(I) 5x – 2y = 1
(II) 3x + 3y = 9

Wir haben die erste Gleichung mit 1,5 multipliziert, damit der Koeffizient (Vorzahl) der Variablen y bis auf das Vorzeichen übereinstimmt.

$(I) 5x - 2y = 1 |\cdot 1,5$
$(II) 3x + 3y = 9$
—————————
$(I) 7,5x - 3y = 1,5$
$(II) 3x + 3y = 9$

Danach haben wir die beiden Gleichungen addiert, dadurch wurde y eliminieirt und wir konnten nach x auflösen:

$(I) 7,5x - 3y = 1,5$
$(II) 3x + 3y = 9 (I) + (II)$
———————————–
$10,5x = 10,5 |: 10,5$
$\Leftrightarrow \color{red}{\underline{\underline{x = 1}}}$

Beim Gauss-Algorithmus machen wir das gleiche. Dabei sparen wir uns Schreibarbeit, indem wir die Variablen nur in die Kopfzeile und die Koeffizienten in die Tabelle darunter schreiben: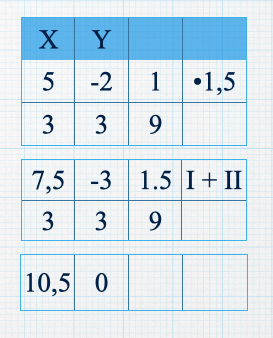

Genauso gehen wir auch mit mehreren Variablen vor. Dabei geht es immer darum, in der untersten Zeile nur noch eine Zahl und den Rest Nullen zu haben. Die Umformung soll also ergeben:
$\begin{array}{ccc|c}x_1 & x_2 & x_3 & \\ \hline \\ * & * & * & * \\ 0 & * & * & * \\ 0 & 0 & * & * \end{array}$

Dabei ist es egal, in welcher Spalte die Nullen stehen. Das Sternchen * bedeutet dabei irgendeine Zahl.
Wir können den Gauss-Algorithmus zum Lösen beliebiger linearer Gleichungssysteme einsetzen.

Dazu könnt ihr euch das 📽️Video Gauss-Algorithmus ganz einfach erklärt ansehen.

Regeln des Gauß Algorithmus

Dabei wird zeilenweise gearbeitet. Zeilen darf man:
– vertauschen
– mit einer Zahl multiplizieren
– durch eine Zahl dividieren
– addieren
– subtrahieren
Spalten dürfen ebenfalls vertauscht werden, wenn die Variable x_i mitgenommen wird.

Beispiel Gauß Algorithmus:

$7x_1 + 3x_2 - 5x_3 = -12$
$-x_1 - 2x_2 + 4x_3 = 5$
$-4x_1 + x_2 -3x_3 = 1$

Hier haben wir also drei Gleichungen mit drei Variablen.

Rechenschema Gauß Algorithmus:

\begin{array}{ccc |c}x_1 & x_2 & x_3 & \\ \hline \\ 7 & 3 & -5 & -12 \\ -1 & -2 & 4 & 5 \\ -4 & 1 & -3 & 1 \end{array}

\begin{array}{ccc|cc}x_1 & x_2 & x_3 & & \\ \hline \\ 7 & 3 & -5 & -12 & | \cdot 4 \\ -1 & -2 & 4 & 5 & | \cdot 28 \\ -4 & 1 & -3 & 1 & | \cdot 7 \\ \hline \\ 28 & 12 & -20 & -48 & \\ -28 & -56 & 112 & 140 & II + I \\ -28 & 7 & -21 & 7 & III + 1 \\ \hline \\ 28 & 12 & -20 & -48 & | : 4 \\ 0 & -44 & 92 & 92 & | :4 \\ 0 & 19 & -41 & -41 & \\ \hline \\ 7 & 3 & -5 & -12 & \\ 0 & -11 & 23 & 23 & | \cdot 19 \\ 0 & 19 & -41 & -41 & | \cdot 11 \\ \hline \\ 7 & 3 & -5 & -12 & \\ 0 & -209 & 437 & 437 & | :19 \\ 0 & 209 & -451 & -451 & III + II \\ \hline \\ 7 & 3 & -5 & -12 & \\ 0 & -11 & 23 & 23 & \\ 0 & 0 & -14 & -14 & \\ \hline \end{array}

Ermittlung der Lösung durch Rückwärtseinsetzen:

$-14x_3 = -14$
$\Leftrightarrow \underline{\underline{ x_3 = 1 }}$

$-11x_2 + 23 \cdot 1 = 23$
$\Leftrightarrow -11x_2 = 0$ $\Leftrightarrow \underline{\underline{x_2 = 0 }}$

$7x_1 + 3 \cdot 0 - 5 \cdot 1 = -12$
$\Leftrightarrow 7x_1 = -7$ $\Leftrightarrow \underline{\underline{x_1 = -1 }}$

L = \{ -1; 0; 1 \}

Probe:
$7 \cdot (-1) + 3 \cdot 0 -5 \cdot 1 = -12 \,$ (w)
$-1 \cdot (-1) - 2 \cdot 0 + 4 \cdot 1 = 5 \,$ (w)
$-4 \cdot (-1) + 1 \cdot 0 - 3 \cdot 1 = 1 \,$ (w)
Dazu kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.

Tipps für blutige Anfänger des Gauß Algorithmus:

Der Gauß Algorithmus ist nicht einfach, deshalb gebe ich hier ein paar Hinweise. Die Vorgehensweise kann dabei in einzelne kleine Schritte zerlegt werden:

Man kann Brüche vermeiden durch zeilenweise Multiplikation mit dem Hauptnenner.
Die erste Zahl in der ersten Zeile soll positiv sein (ev. mit -1 multiplizieren).
Sorgen Sie durch Multiplikation oder Division dafür, dass in der ersten Spalte alle Zahlen den gleichen Betrag haben. In Zeile 2 und 3 sollte die erste Zahl jedoch negativ sein.
Addieren Sie zur 2. und zur 3. Zeile jeweils die erste. Dadurch entstehen in der ersten Spalte 2 Nullen.
Die zweite Zahl in der 2. Zeile soll positiv sein, dies können Sie eventuell erreichen, indem Sie mit -1 multiplizieren.
Sorgen Sie durch Multiplikation oder Division dafür, dass ab der 2. Zeile in der zweiten Spalte alle Zahlen den gleichen Betrag haben. In Zeile 3 sollte die zweite Zahl jedoch negativ sein.
Addieren Sie zur 3. Zeile die 2. Zeile. Dadurch entsteht in der 3. Zeile die 2. Null.
Ermittlung der Lösung durch Rückwärts einsetzen.

Die gleiche Vorgehensweise kann man ebenfalls auf Systeme mit mehr als drei Gleichungen übertragen.

Die Umformungen kann man auch anders durchführen. Das „wie“ ist hierbei ganz dem Geschick des Mathematikers überlassen. Durch intensive Übung gelangt man schließlich zu einem optimalen Weg. Brüche sollte man dabei möglichst vermeiden, um keine unnötigen Fehler zu riskieren. Wer fit ist, kann auch mehrere Umformungen gleichzeitig machen, dadurch ist weniger zu schreiben, die Fehlerquote steigt aber.

tausche: $\rightleftarrows$

\begin{array}{ccc|ccc}x_1 & x_2 & x_3 & & & \\ \hline \\ 7 & 3 & -5 & -12 & & \\ -1 & -2 & 4 & 5 & | \cdot (-1) & I \rightleftarrows II \\ -4 & 1 & -3 & 1 & & \\ \hline \\ 1 & 2 & -4 & -5 & & \\ 7 & 3 & -5 & -12 & & II -7 \cdot I \\ -4 & 1 & -3 & 1 & & III + 4 \cdot I \\ \hline \\ 1 & 2 & -4 & 5 & & \\ 0 & -11 & 23 & 23 & & | \cdot 9 \\ 0 & 9 & -19 & -19 & & | \cdot 11 \\ \hline \\ 1 & 2 & -4 & -5 & & \\ 0 & -99 & 207 & 207 & & | :9 \\ 0 & 99 & -209 & -209 & & III + II \\ \hline \\ 1 & 2 & -4 & 5 & & \\ 0 & -11 & 23 & 23 & & \\ 0 & 0 & -2 & -2 & & \\ \hline \end{array}

Ermittlung der Lösung durch Rückwärtseinsetzen:

$-2x_3 = -2$
$\Leftrightarrow \underline{\underline{x_3 = 1}}$

$-11x_2 + 23 \cdot 1 = 23$
$\Leftrightarrow -11y = 0$ $\Leftrightarrow \underline{\underline{x_2 = 0}}$

$x_1 + 2 \cdot 0 - 4 \cdot 1 = -5$
$\Leftrightarrow x_1 = -7$ $\Leftrightarrow \underline{\underline{x_1 = -1}}$

L = \{-1; 0; 1\}

Probe:
$7 \cdot (-1) + 3 \cdot 0 - 5 \cdot 1 = -12$
$-1 \cdot (-1) - 2 \cdot 0 + 4 \cdot 1 = 5$ $-4 \cdot (-1) + 1 \cdot 0 - 3 \cdot 1 = 1$

Beispiel 1 für den Gauß Algorithmus: (leicht)

$2x_1 - 3x_2 +4x_3 = 8$
$3x_1 +4x_2 - 5x_3 = -4$ $4x_1 -6x_2 + 3x_3 = 1$

\begin{array}{ccc|ccc} x_1 & x_2 & x_3 & & & \\ \hline \\ 2 & -3 & 4 & 8 & & | \cdot 6 \\ 3 & 4 & -5 & -4 & & | \cdot 4 \\ 4 & -6 & 3 & 1 & & | \cdot 3 \\ \hline \\ 12 & -18 & 24 & 48 & & | :6 \\ 12 & 16 & -20 & -16 & & II - I \\ 12 & -18 & 9 & 3 & & III - I \\ \hline \\ 2 & -3 & 4 & 8 & & \\ 0 & 34 & -44 & -64 & & \\ 0 & 0 & -15 & -45 & & \\ \hline \end{array}

Ermittlung der Lösung durch Rückwärtseinsetzen:

$-15x_3 = -45$
$\Leftrightarrow \underline{\underline{x_3 = 3}}$

$34x_2 - 44 \cdot 3 = -64$
$\Leftrightarrow 34x_2 = 68$ $\Leftrightarrow \underline{\underline{x_2 = 2}}$

$2x_1 - 3 \cdot 2 + 4\cdot 3 = 8$
$\Leftrightarrow 2x_1 = 2$ $\Leftrightarrow \underline{\underline{x_1 = 1}}$

Probe:
$2 \cdot 1 - 3 \cdot 2 + 4 \cdot 3 = 8$ (w)
$3 \cdot 1 - 4 \cdot 2 - 5 \cdot 3 = -4$ (w) $4 \cdot 1 - 6 \cdot 2 + 3 \cdot 3 = 1$ (w)

Beispiel 2:
(mittelschwer)

$3x_1 + 2x_2 - 4x_3 = -2$
$4x_1 - 5x_2 + 3x_3 = 9$ $8x_1 + 7x_2 - 9x_3 = 13$

\begin{array}{ccc|ccc} x_1 & x_2 & x_3 & & & \\ \hline \\ 3 & 2 & -4 & -2 & & | \cdot 8 \\ 4 & -5 & 3 & 9 & & | \cdot 6 \\ 8 & 7 & -9 & 13 & & | \cdot 3 \\ \hline \\ 24 & 16 & -32 & -16 & & | :8 \\ 24 & -30 & 13 & 54 & & II - I \\ 24 & 21 & -27 & 39 & & III - I \\ \hline \\ 3 & 2 & -4 & -2 & & \\ 0 & -46 & 50 & 70 & | :2 & II \rightleftarrows III \\ 0 & 5 & 5 & 55 & & | :5 \\ \hline \\ 3 & 2 & -4 & -2 & & \\ 0 & 1 & 1 & 11 & & | \cdot 23 \\ 0 & -23 & 25 & 35 & & \\ \hline \\ 3 & 2 & -4 & -2 & & \\ 0 & 23 & 23 & 253 & & | :23 \\ 0 & -23 & 25 & 35 & & III + II \\ \hline \\ 3 & 2 & -4 & -2 & & \\ 0 & 1 & 1 & 11 & & \\ 0 & 0 & 48 & 288 & & \\ \hline \end{array}

Ermittlung der Lösung durch Rückwärtseinsetzen:

$48x_3 = 288$
$\Leftrightarrow \underline{\underline{x_3 = 6}}$

$x_2 + 1 \cdot 6 = 11$
$\Leftrightarrow \underline{\underline{x_2 = 5}}$

$3x_1 + 2 \cdot 5 - 4 \cdot 6 = -2$
$\Leftrightarrow 3x_1 = 12$ $\Leftrightarrow \underline{\underline{x_1 = 4}}$

L = \{4; 5; 6\}

Probe:
$3 \cdot 4 + 2 \cdot 5 - 4 \cdot 6 = -2$ (w)
$4 \cdot 4 - 5 \cdot 5 + 3 \cdot 6 = 9$ (w) $8 \cdot 4 + 7 \cdot 5 - 9 \cdot 6 = 13$ (w)

Beispiel 3:
(schwer)

$\frac{1}{2}x_1 - \frac{4}{5}x_2 + \frac{3}{8}x_3 = 4$
$\frac{3}{4}x_1 + \frac{3}{8}x_2 + \frac{1}{5}x_3 = 23$ $\frac{4}{5}x_1 - \frac{1}{2}x_2 + \frac{1}{4}x_3 = 8$

\begin{array}{ccc|ccc} x_1 & x_2 & x_3 & & \\ \hline \\ \frac{1}{2} & - \frac{4}{5} & \frac{3}{8} & 4 & & | \cdot 40 \\ \frac{3}{4} & \frac{3}{8} & \frac{1}{5} & 23 & & | \cdot 40 \\ \frac{4}{5} & - \frac{1}{2} & \frac{1}{4} & 8 & & | \cdot 20 \\ \hline \\ 20 & -32 & 15 & 160 & & | \cdot 12 \\ 30 & 15 & 8 & 920 & & \cdot 8 \\ 16 & -10 & 5 & 160 & & | \cdot 15 \\ \hline \\ 240 & -384 & 180 & 1920 & & | : 12 \\ 240 & 120 & 64 & 7360 & & II - I \\ 240 & -150 & 75 & 2400 & & III - I \\ \hline \\ 20 & -32 & 15 & 160 & & \\ 0 & 504 & -116 & 5440 & & | :4 \\ 0 & 234 & -105 & 480 & & | :3 \\ \hline \\ 20 & -32 & 15 & 160 & & \\ 0 & 126 & -29 & 1360 & & | \cdot 13 \\ 0 & 78 & -35 & 160 & & | \cdot 21 \\ \hline \\ 20 & -32 & 15 & 160 & & \\ 0 & 1638 & -377 & 17680 & & | :13 \\ 0 & 1630 & -735 & 3360 & & III - II \\ \hline \\ 20 & -32 & 15 & 160 & & \\ 0 & 126 & -29 & 1360 & & \\ 0 & 0 & -358 & -14320 & & \\ \hline \end{array}

Ermittlung der Lösung durch Rückwärtseinsetzen:

$-358x_3 = 14320$
$\Leftrightarrow \underline{\underline{x_3 = 40}}$

$126x_2 - 29 \cdot 40 = 1360$
$\Leftrightarrow 126x_2 = 2520$ $\Leftrightarrow \underline{\underline{x_2 = 20}}$

$20x_1 - 32 \cdot 20 + 15 \cdot 40 = 160$
$\Leftrightarrow 20x_1 = 200$ $\Leftrightarrow \underline{\underline{x_1 = 10}}$

L = \{10; 20; 40\}

Probe:
$\frac{1}{2} \cdot 10 - \frac{4}{5} \cdot 20 + \frac{3}{8} \cdot 40 = 40$
$\Leftrightarrow 5 - 16 + 15 = 4$ (w) $\frac{3}{4} \cdot 10 + \frac{3}{8} \cdot 20 + \frac{1}{5} \cdot 40 = 23$ $\Leftrightarrow \frac{15}{2} + \frac{15}{2} + 8 = 23$ (w)
$\frac{4}{5} \cdot 10 - \frac{1}{2} \cdot 20 \frac{1}{4} \cdot 40 = 8$
$\Leftrightarrow 8 - 10 + 10 = 8$ (w)

Anwendungsbeispiele für den Gauß Algorithmus:

Schließlich zeige ich hie die Anwendung des Gauß-Algorithmus zur Berechnung der Funktionsgleichung einer ganzrationalen Funktion, von der 4 Punkte bekannt sind.

Anwendungsbeispiel 1:

f(x) = a_3x^3 + a_2x^2 + a_1x + a_0

$P_1(1|4) \Rightarrow f(1) = 1a_3 + 1a_2 + 1a_1 + 1a_0 = 4$
$P_2(2|2) \Rightarrow f(2) = 8a_3 + 4a_2 + 2a_1 +1a_0 = 2$ $P_3(4|4) \Rightarrow f(4) = 64a_3 +16a_2 + 4a_1 + 1a_0 = 4$
$P_4(5|20) \Rightarrow f(5) = 125a_3 +25a_2 +5a_1 + 1a_0 = 20$

\begin{array}{cccc|ccc} a_0 & a_1 & a_2 & a_3 & & & \\ \hline \\ 1 & 1 & 1 & 1 & 4 & & \\ 1 & 2 & 4 & 8 & 2 & & II -I \\ 1 & 4 & 16 & 64 & 4 & & III - I \\ 1 & 5 & 25 & 125 & 20 & & IV - I \\ \hline \\ 1 & 1 & 1 & 1 & 4 & & \\ 0 & 1 & 3 & 7 & -2 & & \\ 0 & 3 & 15 & 63 & 0 & & III - 3 \cdot II \\ 0 & 4 & 24 & 124 & 16 & & IV - 4 \cdot II \\ \hline \\ 1 & 1 & 1 & 1 & 4 & & \\ 0 & 1 & 3 & 7 & -2 & & \\ 0 & 0 & 6 & 42 & 6 & & \\ 0 & 0 & 12 & 96 & 24 & & IV - 2 \cdot III \\ \hline \\ 1 & 1 & 1 & 1 & 4 & & \\ 0 & 1 & 3 & 7 & -2 & & \\ 0 & 0 & 6 & 42 & 6 & & \\ 0 & 0 & 0 & 12 & 12 & & \\ \hline \end{array}

12a_3 = 12 \Leftrightarrow \underline{\underline{a_3 = 1}}

$6a_2 + 42a_3 = 6$
$\Leftrightarrow 6a_2 + 42 = 6 \, \, | -42$ $\Leftrightarrow 6a_2 = -36 \, \, | :6$
$\Leftrightarrow \underline{\underline{a_2 = -6}}$

$1_1 + 3a_2 + 7a_3 = -2$
$\Leftrightarrow a_1 - 18 + 7 = -2$ $\Leftrightarrow a_1 - 11 = -2 \, \, | +11$
$\Leftrightarrow \underline{\underline{a_1 = 9}}$

$a_0 + a_1 + a_2 + a_3 = 4$
$\Leftrightarrow a_0 + 9 - 6 + 1 = 4$ $\Leftrightarrow a_0 + 4 = 4 \, \, | -4$
$\Leftrightarrow \underline{\underline{a_0 = 0}}$

\underline{\underline{f(x) = x^3 - 6x^2 + 9x}}

Beispiel 2:

f(x) = a_3x^3 + a_2x^2 + a_1x + a_0

$P_1(1 | \frac{11}{2}) \Rightarrow f(1) = 1a_3 +1a_2 + 1a_1 + 1a_0 = -\frac{11}{2}$
$P_2(-1 | \frac{9}{2}) \Rightarrow f(-1) = -1a_3 + 1a_2 - 1a_1 + 1a_0 = \frac{9}{2}$ $P_3(-2 | 8) \Rightarrow f(-2) = -8a_3 + 4a_2 - 2a_1 + 1a_0 = 8$ $P_4(-3| \frac{5}{2}) \Rightarrow f(-3) = -27a_3 + 9a_2 -3a_1 + 1a_0 = \frac{5}{2}$

\begin{array}{cccc|ccc} a_0 & a_1 & a_2 & a_3 & & & \\ \hline \\ 1 & 1 & 1 & 1 & - \frac{11}{2} & & | \cdot 2 \\ 1 & -1 & 1 & -1 & \frac{9}{2} & & | \cdot 2 \\ 1 & -2 & 4 & -8 & 8 & & | \cdot 2 \\ 1 & -3 & 9 & -27 & \frac{5}{2} & & | \cdot 2 \\ \hline \\ 2 & 2 & 2 & 2 & -11 & & \\ 2 & -2 & 2 & -2 & 9 & & II - I \\ 2 & -4 & 8 & -16 & 16 & & III - I \\ 2 & -6 & 18 & -54 & 5 & & IV - I \\ \hline \\ 2 & 2 & 2 & 2 & -11 & & \\ 0 & -4 & 0 & -4 & 20 & & | :(-2) \\ 0 & -6 & 6 & -18 & 27 & & | :3 \\ 0 & -8 & 16 & -56 & 16 & & | :4 \\ \hline \\2 & 2 & 2 & 2 & -11 & & \\ 0 & 2 & 0 & 2 & -10 & & \\ 0 & -2 & 2 & -6 & 9 & & III + II \\ 0 & -2 & 4 & -14 & 4 & & IV + II \\ \hline \\ 2 & 2 & 2 & 2 & -11 & & \\ 0 & 2 & 0 & 2 & -10 & & \\ 0 & 0 & 2 & -4 & -1 & & \\ 0 & 0 & 4 & -12 & -6 & & IV - 2 \cdot III \\ \hline \\ 2 & 2 & 2 & 2 & -11 & & \\ 0 & 2 & 0 & 2 & -10 & & \\ 0 & 0 & 2 & -4 & -1 & & \\ 0 & 0 & 0 & -4 & -4 & & \\ \hline \end{array}

-4a_3 = - 4 \Leftrightarrow \underline{\underline{a_3 = 1}}

$2a_2 - 4a_3 = -1$
$\Leftrightarrow 2a_2 - 4 = -1 \, \, | +4$ $\Leftrightarrow 2a_2 = 3 \, \, | :2$
$\Leftrightarrow \underline{\underline{a_2 = \frac{3}{2}}}$

$2a_1 + 2a_3 = -10$
$\Leftrightarrow 2a_1 + 2 = -10 \, \, | -2$ $\Leftrightarrow 2a_1 = -12 \, \, | :2$
$\Leftrightarrow \underline{\underline{a_1 = -6}}$

$2a_0 + 2a_1 + 2a_2 + 2a_3 = -11$
$\Leftrightarrow 2a_0 - 12 + 3 + 2 = -11$ $\Leftrightarrow 2a_0 - 7 = - 11 \, \, | +7$ $\Leftrightarrow 2a_0 = -4 \, \, | :2$ $\Leftrightarrow \underline{\underline{a_0 = -2}}$

\underline{\underline{f(x) = x^3 + \frac{3}{2}x^2 -6x - 2}}

Beispiel 3:

f(x) = a_3x^3 + a_2x^2 + a_1x + a_0

$P_1(-1 | -16) \Rightarrow f(-1) = -1a_3 + 1a_2 - 1a_1 + 1a_0 = -16$
$P_2(2 | 11) \Rightarrow f(2) = 8a_3 + 4a_2 + 2a_1 + 1a_0 = 11$ $P_3(4 | -11) \Rightarrow f(4) = 64a_3 + 16a_2 + 2a_1 + 1a_0 = -11$
$P_4(6 | -9) \Rightarrow f(6) = 216a_3 + 36a_2 + 5a_1 + 1a_0 = -9$

\begin{array}{cccc|ccc} a_0 & a_1 & a_2 & a_3 & & & \\ \hline \\ 1 & -1 & 1 & -1 & -16 && \\ 1 & 2 & 4 & 8 & 1 & & II - I \\ 1 & 4 & 16 & 64 & -11 & & III - I \\ 1 & 6 & 36 & 216 & -9 & & IV - I \\ \hline \\ 1 & -1 & 1 & -1 & -16 & & \\ 0 & 3 & 3 & 9 & 27 & & | :3 \\ 0 & 5 & 15 & 65 & 5 & & | :5 \\ 0 & 7 & 35 & 217 & 7 & & | :7 \\ \hline \\ 1 & -1 & 1 & -1 & -16 & & \\ 0 & 1 & 1 & 3 & 9 & & \\ 0 & 1 & 3 & 13 & 1 & & III - II \\ 0 & 1 & 5 & 31 & 1 & & IV - II \\ \hline \\ 1 & -1 & 1 & -1 & -16 & & \\ 0 & 1 & 1 & 3 & 9 & & \\ 0 & 0 & 2 & 10 & -8 & & \\ 0 & 0 & 4 & 28 & -8 & & IV - 2 \cdot III \\ \hline \\ 1 & -1 & 1 & -1 & -16 & & \\ 0 & 1 & 1 & 3 & 9 & & \\ 0 & 0 & 2 & 10 & -8 & & \\ 0 & 0 & 0 & 8 & 8 & & \\ \hline \end{array}

8a_3 = 8 \Leftrightarrow \underline{\underline{a_3 = 1}}

$2a_2 + 10a_3 = -8$
$\Leftrightarrow 2a_2 + 10 = -8 \, \, | -10$ $2a_2 = -18 \, \, : 2$
$\Leftrightarrow \underline{\underline{a_2 = -9}}$

$a_1 + a_2 + 3a_3 = 9$
$\Leftrightarrow a_1 - 9 + 3 = 9$ $\Leftrightarrow a_1 - 6 = 9 \, \, | +6$ $\Leftrightarrow \underline{\underline{a_1 = 15}}$

$a_0 - a_1 + a_2 - a_3 = -16$
$\Leftrightarrow a_0 - 15 - 9 - 1 = -16$ $\Leftrightarrow a_0 - 25 = -16 \, \, | +25$ $\Leftrightarrow \underline{\underline{a_0 = 9}}$

\underline{\underline{f(x) = x^3 - 9x^2 +15x +9}}

Anwendungsbeispiel 4:

$f(x) = a_3x^3 + a_2x^2 +a_1x + a_0$
$P_1(-1 | 7) \Rightarrow f(-1) = -1a_3 + 1a_2 -1a_1 + 1a_0 = 7$ $P_2(-2 | 6) \Rightarrow f(-2) = -8a_3 + 4a_2 - 2a_1 + 1a_0 = 6$ $P_3(3 | 1) \Rightarrow f(3) = 27a_3 + 9a_2 + 3a_1 + 1a_0 = 1$ $P_4(-3 | -2) \Rightarrow f(-3) = -27a_3 + 9a_2 - 3a_1 + 1a_0 = -2$

\begin{array}{cccc|ccc} a_0 & a_1 & a_2 & a_3 & & & \\ \hline \\ 1 & -1 & 1 & -1 & 7 & & \\ 1 & -2 & 4 & -8 & 6 & & II - I \\ 1 & 3 & 9 & 27 & 1 & & III - I \\ 1 & -3 & 9 & -27 & -2 & & IV - I \\ \hline \\ 1 & -1 & 1 & -1 & 7 & & \\ 0 & -1 & 3 & -7 & -1 & & \\ 0 & 4 & 8 & 28 & -6 & & III + 4 \cdot II \\ 0 & -2 & 8 & -26 & -9 & & IV - 2 \cdot II \\ \hline \\ 1 & -1 & 1 & -1 & 7 & & \\ 0 & -1 & 3 & -7 & -1 & & \\ 0 & -1 & 3 & -7 & -1 & & \\ 0 & 0 & 20 & 0 & -10 & & \\ 0 & 0 & 2 & -12 & -7 & & \\ \hline \end{array}

20a_2 = -10 \Leftrightarrow \underline{\underline{a_2 = - \frac{1}{2}}}

$2a_2 - 12a_3 = -7$
$\Leftrightarrow -1 -12a_3 = -7 \, \, +1$ $\Leftrightarrow 12a_3 = -6 \, \, | :(-12)$ $\Leftrightarrow \underline{\underline{a_3 = \frac{1}{2}}}$

$-a_1 + 3a_2 -7a_3 = -1$
$\Leftrightarrow -a_1 - \frac{3}{2} - \frac{7}{2} = -1$ $\Leftrightarrow -a_1 -5 = -1 \, \, | +5$ $\Leftrightarrow -a_1 = 4 \, \, | :(-1)$ $\Leftrightarrow \underline{\underline{a_1 = -4}}$

$a_0 - a_1 +a_2 - a_3 = 7$ $\Leftrightarrow a_0 + 4 - \frac{1}{2} - \frac{1}{2} = 7$ $\Leftrightarrow a_0 + 3 = 7\, \, | -3$
$\Leftrightarrow \underline{\underline{a_0 = 4}}$

\underline{\underline{f(x) = \frac{1}{2}x^3 - \frac{1}{2}x^2 -4x + 4}}

Beispiel 5:

$f(x) = a_3x^3 + a_2x^2 +a_1x + a_0$
$P_1(2 | 22) \Rightarrow f(2) = 8a_3 + 4a_2 + 2a_1 + 1a_0 = 22$ $P_2(4 | 44) \Rightarrow f(4) = 64a_3 + 16a_2 + 4a_1 + 1a_0 = 44$ $P_(-4 | 4) \Rightarrow f(-4) = -64a_3 + 16a_2 - 4a_1 + 1a_0 = 4$ $P_4(8 | 40) \Rightarrow f(8) = 512a_3 + 64a_2 +8a_1 + 1a_0 = 40$

\begin{array}{cccc|ccc} a_0 & a_1 & a_2 & a_3 & & & \\ \hline \\ 1 & 2 & 4 & 8 & 22 & & \\ 1 & 4 & 16 & 64 & 44 & & II - I \\ 1 & -4 & 16 & -64 & 4 & & III - I \\ 1 & 8 & 64 & 512 & 40 && IV - I \\ \hline \\ 1 & 2 & 4 & 8 & 22 & & \\ 0 & 2 & 12 & 56 & 22 & & \\ 0 & -6 & 12 & -72 & -18 & & III + 3 \cdot II \\ 0 & 6 & 60 & 504 & 18 & & IV - 3 \cdot II \\ \hline \\ 1 & 2 & 4 & 8 & 22 & & \\ 0 & 2 & 12 & 56 & 22 & & \\ 0 & 0 & 48 & 96 & 48 & & \\ 0 & 0 & 24 & 336 & -48 & & IV - \dfrac{1}{2} \cdot III \\ \hline \\ 1 & 2 & 4 & 8 & 22 & & \\ 0 & 2 & 12 & 56 & 22 & & \\ 0 & 0 & 48 & 96 & 48 & & \\ 0 & 0 & 0 & 288 & -72 & & \\ \hline \end{array}

Die Funktionsgleichung:

288a_3 = -72 \Leftrightarrow \underline{\underline{a_3 = -\frac{1}{4}}}

$48a_2 + 96a_3 = 48$
$\Leftrightarrow 48a_2 - 24 = 48 \, \, +24$ $\Leftrightarrow 48a_2 = 72 \, \, | :48$ $\Leftrightarrow \underline{\underline{a_2 = \frac{3}{2}}}$

$2a_1 + 12a_2 +56a_3 = 22$
$\Leftrightarrow 2a_1 + 18 - 14 = 22$ $\Leftrightarrow 2a_1 + 4 = 22 \, \, | -4$ $\Leftrightarrow 2a_1 = 18 \, \, | :2$ $\Leftrightarrow \underline{\underline{a_1 = 9}}$

$a_0 + 2a_1 + 4a_2 + 8a_3 = 22$
$\Leftrightarrow a_0 + 18 + 6 - 2 = 22$ $\Leftrightarrow a_0 + 22 = 22 \,\, | -22$ $\Leftrightarrow \underline{\underline{a_0 = 0}}$

f(x) = - \frac{1}{4}x^3 + \frac{3}{2}x^2 + 9x

Anwendungsbeispiel 6:

$f(x) = a_3x^3 + a_2x^2 + a_1x + a_0$
$P_1(1 | 0) \Rightarrow f(1) = 1a_3 + 1a_2 +1a_1 + 1a_0 = 0$ $P_2(-1 | -2) \Rightarrow f(-1) = -1a_3 + 1a_2 - 1a_1 +1a_0 = -2$ $P_3(2 | 16) \Rightarrow f(2) = 8a_3 + 4a_2 +2a_1 +1a_0 = 16$ $P_4(-3 | -4) \Rightarrow f(-3) = -27a_3 + 9a_2 -3a_1 + 1a_0 = -4$

\begin{array}{cccc|ccc} a_0 & a_1 & a_2 & a_3 & & & \\ \hline \\ 1 & 1 & 1 & 1 & 0 & & \\ 1 & -1 & 1 & -1 & -2 & & II - I \\ 1 & 2 & 4 & 8 & 16 & & III - I \\ 1 & -3 & -9 & -27 & -4 & & IV - I \\ \hline \\ 1 & 1 & 1 & 1 & 0 & & \\ 0 & -2 & 0 & -2 & -2 & & \\ 0 & 1 & 3 & 7 & 16 & & III + \dfrac{1}{2} \cdot II \\ 0 & -4 & 8 & -28 & -4 & & \\ \hline \\ 1 & 1 & 1 & 1 & 0 & & \\ 0 & -2 & 0 & -2 & -2 & & \\ 0 & 0 & 3 & 6 & 15 & & & | :3 \\ 0 & 0 & 8 & -24 & 1 & & | :8 \\ \hline \\ 1 & 1 & 1 & 1 & 0 & & \\ 0 & -2 & 0 & -2 & -2 & & \\ 0 & 0 & 1 & 2 & 5 & & \\ 0 & 0 & 1 & -3 & 0 & & IV - III \\ \hline \\ 1 & 1 & 1 & 1 & 0 & & \\ 0 & -2 & 0 & -2 & -2 & & \\ 0 & 0 & 1 & 2 & 5 & & \\ 0 & 0 & 0 & -5 & -5 & & \\ \hline \end{array}

-5a_3 = -5 \Leftrightarrow \underline{\underline{a_3 = 1}}

$a_2 = 2a_3 = 5$
$\Leftrightarrow a_2 + 2 = 5 \, \, |-2$ $\Leftrightarrow \underline{\underline{a_2 = 3}}$

$-2a_1 -2a_3 = -2$
$\Leftrightarrow -2a_1 -2 = -2 \, \, +2$ $\Leftrightarrow -2a_1 = 0$ $\Leftrightarrow \underline{\underline{a_1 = 0}}$

$a_0 + a_1 + a_2 + a_3 = 0$
$\Leftrightarrow a_0 + 3 + 1 = 0$ $\Leftrightarrow a_0 + 4 = 0 \, \, | -4$ $\Leftrightarrow \underline{\underline{a_0 = -4}}$

f(x) = x^3 + 3x^2 - 4

Beispiel 7:

$f(x) = a_3x^3 + a_2x^2 +a_1x + a_0$
$P_1(1 | 1) \Rightarrow f(1) = 1a_3 + 1a_2 + 1a_1 + 1a_0 = 1$ $P_2(2 | 0) \Rightarrow f(2) = 8a_3 + 4a_2 + 2a_1 + 1a_0 = 0$ m $P_3(-2 | 4) \Rightarrow f(-2) = -8a_3 + 4a_2 - 2a_1 + 1a_0 = 4$ $P_4(3 | 9) \Rightarrow f(3) = 27a_3 + 9a_2 + 3a_1 + 1a_0 = 9$

\begin{array}{cccc|ccc}a_0 & a_1 & a_2 & a_3 & & & \\ \hline \\ 1 & 1 & 1 & 1 & 1 & & \\ 1 & 2 & 4 & 8 & 0 & & II -I \\ 1 & -2 & 4 & -8 & 4 & & III - I \\ 1 & 3 & 9 & 27 & 9 & & IV - I \\ \hline \\ 1 & 1 & 1 & 1 & 1 & & \\ 0 & 1 & 3 & 7 & -1 & & \\ 0 & -3 & 3 & -9 & 3 & & III + 3 \cdot II \\ 0 & 2 & 8 & 26 & 8 & & IV - 2 \cdot II \\ \hline \\ 1 & 1 & 1 & 1 & 1 & & \\ 0 & 1 & 3 & 7 & -1 & & \\ 0 & 0 & 12 & 12 & 0 & & \\ 0 & 0 & 2 & 12 & 10 & & IV - \dfrac{1}{6} \cdot III \\ \hline \\ 1 & 1 & 1 & 1 & 1 & & \\ 0 & 1 & 3 & 7 & -1 & & \\ 0 & 0 & 12 & 12 & 0 & & \\ 0 & 0 & 0 & 10 & 10 && \\ \hline \end{array}

10a_3 = 10 \Leftrightarrow \underline{\underline{a_3 = 1}}

$12a_2 + 12a_3 0 0$
$\Leftrightarrow 12a_2 + 12 = 0 \, \, | -12$ $\Leftrightarrow 12a_2 = -12 \, \, | :12$ $\Leftrightarrow \underline{\underline{a_2 = -1}}$

$a_1 + 3a_2 +7a_3 = -1$
$\Leftrightarrow a_1 - 3 + 7 = -1$ $\Leftrightarrow a_1 + 4 = -1 \, \, | -4$ $\Leftrightarrow \underline{\underline{a_1 = -5}}$

$a_0 + a_1 + a_2 + a_3 = 1$
$\Leftrightarrow a_0 -5 -1 + 1 = 1$ $\Leftrightarrow a_0 - 5 = 1 \, \, | +5$ $\Leftrightarrow \underline{\underline{a_0 = 6 }}$

\underline{\underline{f(x) = x^3 - x^2 - 5x + 6}}

Anwendungsbeispiel 8:

$f(x) = a_3x^3 + a_2x^2 + a_1x + a_0$
$P_1(1 | 6) \Rightarrow f(1) = 1a_3 + 1a_2 + 1a_1 + 1a_0 = 6$ $P_2(3 | -4) \Rightarrow f(3) = 27a_3 + 9a_2 + 3a_1 + 1a_0 = -4$ $P_3(- \frac{1}{2} | \frac{45}{8}) \Rightarrow f(-\frac{1}{2} = - \frac{1}{8}a_3 + \frac{1}{4}a_2 - \frac{1}{2} + 1a_0 = \frac{45}{8}$ $P_4(- \frac{3}{2} | -\frac{77}{8}) \Rightarrow f(- \frac{3}{2}) = - \frac{27}{8}a_3 + \frac{9}{4}a_2 - \frac{3}{2}a_1 + 1a_0 = - \frac{77}{8}$

\begin{array}{cccc|ccc}a_0 & a_1 & a_2 & a_3 & & & \\ \hline \\ 1 & 1 & 1 & 1 & 6 & & \\ 1 & 3 & 9 & 27 & -27 & & \\ 1 & - \dfrac{1}{2} & \dfrac{1}{4} & - \dfrac{1}{8} & \dfrac{45}{8} & & | \cdot 8 \\ 1 & - \dfrac{3}{2} & \dfrac{9}{4} & - \dfrac{27}{8} & - \dfrac{77}{8} & & | \cdot 8 \\ \hline \\ 1 & 1 & 1 & 1 & 6 & & \\ 2 & 3 & 9 & 27 & -4 & & II - I \\ 8 & -4 & 2 & -1 & 45 & & III - 8 \cdot I \\ 8 & -12 & 18 & -27 & -77 & & IV - 8 \cdot I \\ \hline \\ 1 & 1 & 1 & 1 & 6 & & \\ 0 & 2 & 8 & 26 & -10 & & \\ 0 & -12 & -6 & -9 & -3 & & III + 6 \cdot II \\ 0 & -20 & 10 & -35 & -125 & & IV + 10 \cdot II \\ \hline \\ 1 & 1 & 1 & 1 & 6 & & \\ 0 & 2 & 8 & 26 & -10 & & \\ 0 & 0 & 42 & 147 & -63 & & | :21 \\ 0 & 0 & 90 & 225 & -225 & & | :45 \\ \hline \\ 1 & 1 & 1 & 1 & 6 & & \\ 0 & 2 & 8 & 26 & -10 & & \\ 0 & 0 & 2 & 7 & -3 & & \\ 0 & 0 & 2 & 5 & -5 & & IV - III \\ \hline \\ 1 & 1 & 1 & 1 & 6 & & \\ 0 & 2 & 8 & 26 & -10 & & \\ 0 & 0 & 2 & 7 & -3 & & \\ 0 & 0 & 0 & -2 & -2 & & \\ \hline \end{array}

-2a_3 = -2 \Leftrightarrow \underline{\underline{a_3 =1}}

$2a_2 - 7a_3 = -3$
$\Leftrightarrow 2a_2 + 7 = -3 \, \, | -7$ $\Leftrightarrow 2a_2 = -10 \, \, | :2$ $\Leftrightarrow \underline{\underline{a_2 = -5}}$

$2a_1 + 8a_2 +26a_3 = -10$
$\Leftrightarrow 2a_1 - 40 + 26 = -10$ $\Leftrightarrow 2a_1 - 14 = -10 \, \, | +14$ $\Leftrightarrow 2a_1 = 4 \, \, | :2$ $\Leftrightarrow \underline{\underline{a_1 = 2}}$

$a_0 + a_1 + a_2 + a_3 = 6$ $\Leftrightarrow a_0 + 2 - 5 + 1 = 6$ $\Leftrightarrow a_0 - 2 = 6 \, \, | +2$
$\Leftrightarrow \underline{\underline{a_0 = 8}}$

\underline{\underline{f(x) = x^3 - 5x^2 + 2x + 8}}

Beispiel 9:

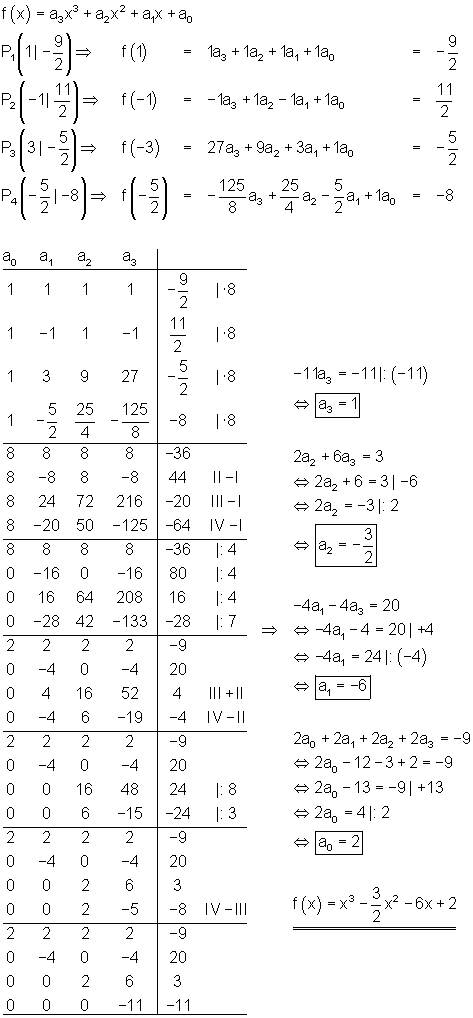
Anwendungsbeispiel 10:

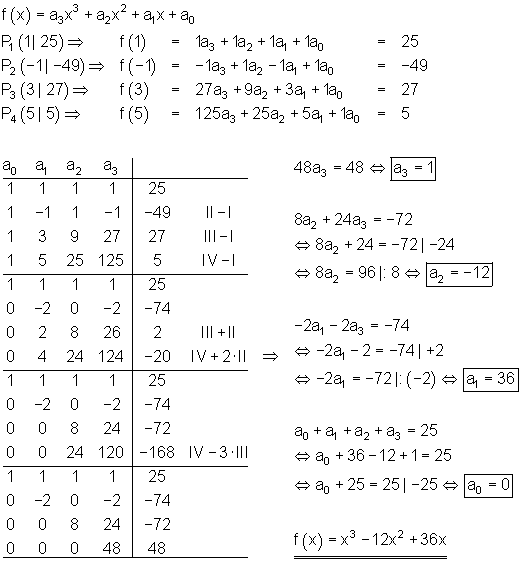
Aufgaben zum Gauß Algorithmus:

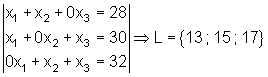
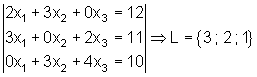
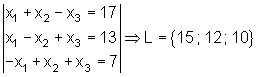
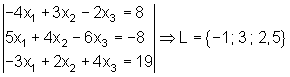
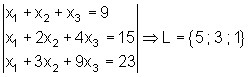
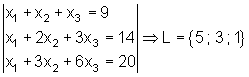
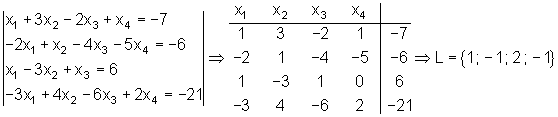
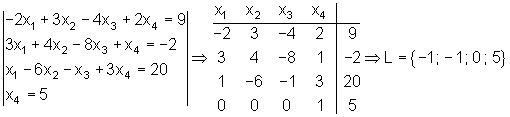
Führe zur Ergebniskontrolle immer die Probe durch!

Den Gauss-Algorithmus kann man auch anwenden, um Aufgaben zu Ganzrationalen Funktionen 3. Grades mittels 4 Punkte zu lösen.
Dazu hier die Theorie: Funktionsgleichung mit bekannten Punkten bestimmen.
Hier findest du eine Übersicht über alle Beiträge zum Thema lineare Gleichungen.
Und hier eine Übersicht über alle Beiträge zu Ganzrationalen Funktionen.

Gauss-Algorithmus leicht verständlich erklärt