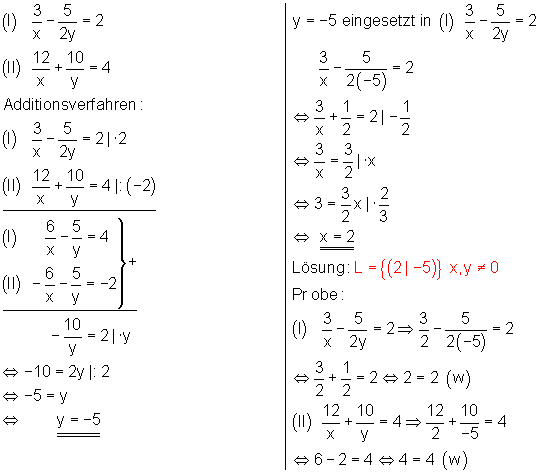In diesem Beitrag erkläre ich anhand vieler Beispiele, wie man Lineare Gleichungen mit zwei Gleichungen und zwei Variablen lösen kann. Dazu gehören das Additionsverfahren, Gleichsetzungsverfahren, zeichnerisches Verfahren und das Einsetzverfahren. Schließlich verlinke ich Aufgaben.
- Lösungsschritte für das Additionsverfahren in 2 Varianten.
- Gleichsetzungsverfahren in 2 Varianten.
- Einsetzverfahren in 2 Varianten
- Zeichnerische Verfahren.
- Beispiele für geeignete Lösungsverfahren
- Gleichungssysteme ohne eindeutige Lösung
- und mit unendlichen Lösungen.
Lineare Gleichungssysteme mit 2 Variablen mit Additionsverfahren lösen Variante 1
Beispiel:
(I) 5x – 2y = 1
(II) 3x + 3y ? 9
1. Beim Additionsverfahren formt man die Gleichungen zuerst äquivalent so um. Dadurch stimmen die Koeffizienten (Vorzahlen) der Variablen y bis auf das Vorzeichen überein.
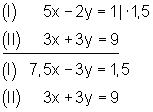
2. Danach addiert man die entstandenen Gleichungen und löst sie nach der Variablen x auf.
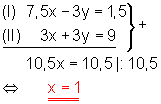
3. Den gefundenen Wert für x setzt man dann in eine der beiden Gleichungen ein und löst nach der Variablen y auf.
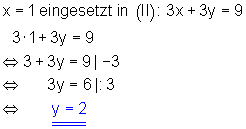
4. Anschließend schreibt man die Lösungsmenge auf.
5. Schließlich führt man die Probe durch Einsetzen durch.
Diese Variante kannst du dir in diesem 
Video: Zwei lineare Gleichungen addieren ansehen.
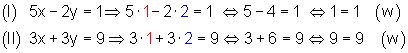
Lineare Gleichungssysteme mit 2 Variablen mit Additionsverfahren lösen Variante 2
Gleichungssystem
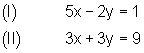
1. Auch beim Additionsverfahren 2 formt man die Gleichungen zuerst äquivalent so um, dass die Koeffizienten (Vorzahlen) der Variablen x bis auf das Vorzeichen übereinstimmen.
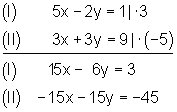
2. Danach addiert man die entstandenen Gleichungen und löst sie nach der Variablen y auf.
3. Den gefundenen Wert für x setzt man dann in eine der beiden Gleichungen ein und löst nach der Variablen x auf.
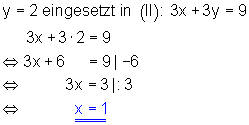
4. Anschließend schreibt man die Lösungsmenge auf.
5. Schließlich führt man die Probe durch Einsetzen durch.
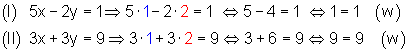
Lineare Gleichungssysteme mit 2 Variablen mit Gleichsetzungsverfahren lösen Variante 1
Gleichungssystem
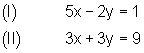
1. Beim Gleichsetzungsverfahren 1 löst man zuerst die beide Gleichungen nach der Variablen x auf.
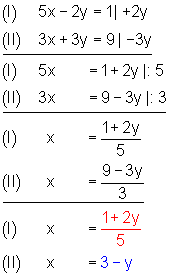
2. Dann setzt man die rechten Seiten beider Gleichungen gleich und löst sie nach der Variablen y auf.
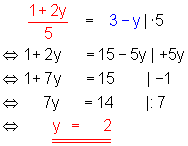
3. Anschließend setzt man den gefundenen Wert für y in eine der beiden Ausgangsgleichungen ein. Dann löst man diese nach der Variablen x auf.
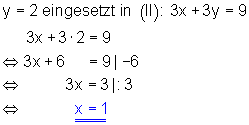
4. Anschließend schreibt man die Lösungsmenge auf.
5. Schließlich führt man die Probe durch Einsetzen durch.
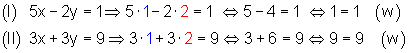
Lineare Gleichungssysteme mit 2 Variablen mit Gleichsetzungsverfahren lösen Variante 2
Gleichungssystem
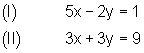
1. Beim Gleichsetzungsverfahren 2 löst man beide Gleichungen zuerst nach der Variablen y auf.
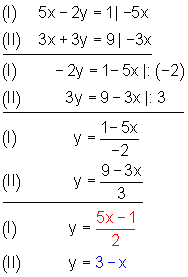
2. Danach setzt man die rechten Seiten beider Gleichungen gleich und und löst sie nach der Variablen x auf.
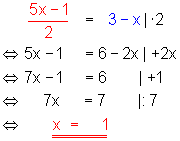
3. Anschließend setzt man den gefundenen Wert für x in eine der beiden Ausgangsgleichungen ein. Danach löst man diese dann nach der Variablen y auf.
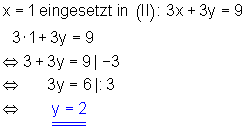
4. Anschließend schreibt man die Lösungsmenge auf.
5. Schließlich führt man die Probe durch Einsetzen durch.
Diese Variante kannst du dir in diesem Video: Zwei lineare Gleichungen gleichsetzen ansehen.
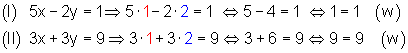
Lineare Gleichungssysteme mit 2 Variablen mit Einsetzverfahren lösen Variante 1
Gleichungssystem
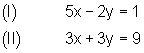
1. Beim Einsetzverfahren löst man die Gleichung (I) zuerst nach der Variablen x auf.
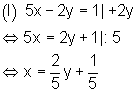
2. Danach setzt man den gefundenen Term der rechten Seite in Gleichung (II) ein und löst nach y auf.
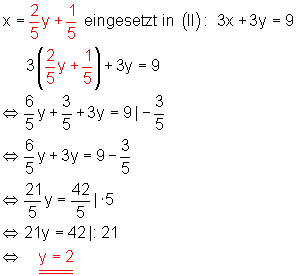
3. Schließlich setzt man den gefundene Wert für y in eine der beiden Ausgangsgleichungen ein. Danach löst man diese nach der Variablen x auf.
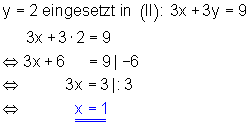
4. Anschließend schreibt man die Lösungsmenge auf.
5. Schließlich führt man die Probe durch Einsetzen durch.
Diese Variante kannst du dir in diesem Video: Zwei lineare Gleichungen mit Einsetzen lösen ansehen.
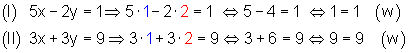
Lineare Gleichungssysteme mit 2 Variablen mit Einsetzverfahren lösen Variante 2
Gleichungssystem
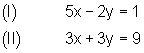
1. Zuerst löst man die Gleichung (II) nach der Variablen y auf.
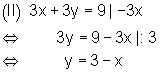
2. Danach setzt man den gefundenen Term der rechten Seite in Gleichung (I) ein und löst nach x auf.
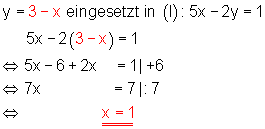
3. Schließlich setzt man den gefundenen Wert für x in eine der beiden Ausgangsgleichungen ein. Danach löst man diese nach der Variablen y auf.
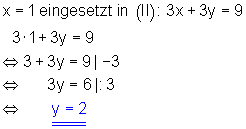
4. Anschließend schreibt man die Lösungsmenge auf.
5. Schließlich führt man die Probe durch Einsetzen durch.
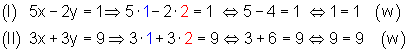
Alle drei Verfahren mit ihren Varianten habe ich auf ein bestimmtes Gleichungssystem angewendet. Man erkennt, dass das Einsetzverfahren in der Variante 2 den geringsten Rechenaufwand erfordert.
Der Rechenaufwand für ein bestimmtes Verfahren hängt von dem zu lösenden Gleichungssystem ab. Deshalb sollte man zuerst überlegen, welches Verfahren sich mit dem geringstem Aufwand durchführen lässt. Dazu bedarf es aber einiger Übungen. Die folgenden Beispiele sollen eine kleine Hilfe dafür sein, das geeignete Lösungsverfahren zu finden.
Beispiele für geeignete Lösungsverfahren
1. Beispiel
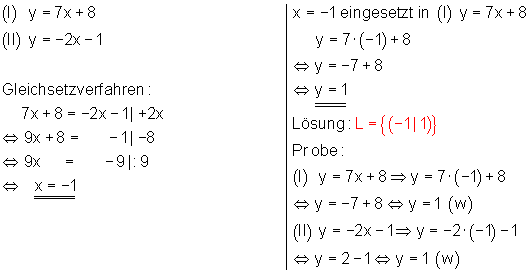
2. Beispiel
(I) \, 2x + 4y = 8
(II) \, 2x - 5y = 35
Additionsverfahren:
(I) \, 2x + 4y = 8
\underline{ (II) \, 2x - 5y = 35 \, \vert \cdot (-1) }
\underline{+ \begin{cases} (I) \, 2x + 4y = 8 \\ (II) \, 2x - 5y = -35 \\\end{cases}}
9y = -27 \, \vert 9
\Leftrightarrow \underline{\underline{y = -3}}
y = -3 eingesetzt in (I) \, 2x + 4y = 8
2x - 12 = 8 \, \vert +12
\Leftrightarrow 2x = 20 \, \vert :2
\Leftrightarrow \underline{\underline{x = 10}}
Lösung: \color{red}{L = \{(10 \vert -3)\}}
Probe:
(I) \, 2x + 4y = 8 \Rightarrow 2 \cdot 10 + 4 \cdot (-3) = 8
\Leftrightarrow 20 - 12 = 8 \Leftrightarrow 8 = 8 (w)
(II) \, 2x - 5y = 35 \Rightarrow 2 \cdot 10 - 5 \cdot (-3) = 35
\Leftrightarrow 20 + 15 = 35 \Leftrightarrow 35 = 35 (w)
Das Additionsverfahren mit anderen Werten kannst du dir in diesem Additionsverfahren: Lineare Gleichungen lösen ansehen.
3. Beispiel
(I) \, x + 2y = 5
(II) \, -x + y = 1
Einsetzverfahren:
(II) \, nach y auflösen
-x + y = 1 \, \vert +x
\Leftrightarrow y = x + 1
eingesetzt in (I) x + 2y = 5
x + 2(x + 1) = 5
\Leftrightarrow x + 2x + 2 = 5 \, \vert -2
\Leftrightarrow 3x = 3 \, \vert :3 \Leftrightarrow \underline{\underline{x = 1}}
x = 1 eingesetzt in (I) \, x + 2y = 5
1 + 2y = 5 \, \vert -1
\Leftrightarrow 2y = 4 \, \vert :2
\Leftrightarrow \underline{\underline{y = 2}}
Lösung: \color{red}{L = \{(1 \vert 2)\}}
Probe:
(I) \, x + 2y = 5 \Rightarrow 1 + 4 = 5
\Leftrightarrow 5 = 5 (w)
(II) \, -x + y = 1 \Rightarrow -1 + 2 = 1 = 35
\Leftrightarrow 1 = 1 (w)
4. Beispiel
Bemerkung:
Das Gleichungssystem besteht aus Bruchtermen. Da der Nenner nicht Null werden darf, muss man die Definitionsmenge angeben. Ein solches Gleichungssystem ist nicht linear.
Zeichnerisches Verfahren
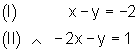
Beide Gleichungen werden nach y aufgelöst.
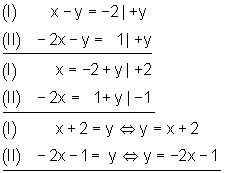
In jede Gleichung werden für x Zahlen eingesetzt. Daraus werden Wertepaare gebildet.
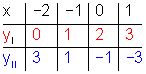
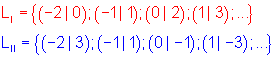
Für jede Gleichung entsprechen die Wertepaare deren Lösungsmenge. Trägt man diese in ein Koordinatensystem ein, so erhält man zwei Geraden. Im Schnittpunkt beider Geraden liegt die gemeinsame Lösung beider Gleichungen. Lösungsmenge: L={(-1|1)}
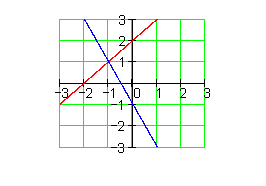
Das zeichnerische Verfahren veranschaulicht den geometrischen Zusammenhang zwischen den Gleichungen und Geraden. Als Lösungsverfahren ist es jedoch meist ungeeignet, da die Koordinaten des gemeinsamen Schnittpunktes oft nur ungenau aus der Grafik abgelesen werden können.
Gleichungssysteme ohne eindeutige Lösung
Die zeichnerische Lösung veranschaulicht den geometrischen Zusammenhang zwischen Gleichungen und Geraden.
Zwei Geraden können unterschiedliche Lagen zueinander haben.
- Sie können sich in einem Punkt schneiden. Dann gibt es, wie obiges Beispiel veranschaulicht, für die beiden linearen Gleichungen genau eine Lösung.
- Sie können parallel zueinander verlaufen. Dann gibt es keinen Punkt, den beide Geraden miteinander haben. Die dazugehörigen Gleichungen dürften demzufolge keine Lösung haben.
- Sie können aufeinander liegen, mit anderen Worten identisch sein. Dann würde jeder Punkt der einen Geraden auch ein Punkt der anderen sein. Die dazugehörigen Gleichungen dürften demzufolge unendlich viele Lösungen haben.
Das Gleichungssystem hat keine Lösung
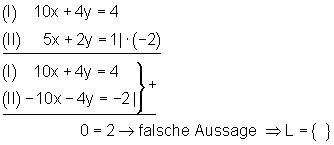
Der Lösungsansatz führt zu einer falschen Aussage. Das bedeutet, es existiert keine Lösung zu dem Gleichungssystem. Anschaulich bedeutet das, die beiden Geraden verlaufen parallel zueinander und haben keinen Punkt gemeinsam.
Das Gleichungssystem hat unendlich viele Lösungen
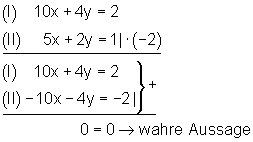
Bei der Addition nach der Äquivalenzumformung heben sich Gleichung (I) und Gleichung (II) gegenseitig auf, das bedeutet sie sind identisch. Jedes Zahlenpaar, das (I) erfüllt, erfüllt folglich auch (II). Anschaulich bedeutet das, die beiden Geraden liegen aufeinander und haben jeden Punkt gemeinsam.
Dazu kannst du auch den Wikipediaartikel zu linearen Gleichungssystemen lesen.
Hier findest du Aufgaben hierzu.
Und hier eine Übersicht über alle Beiträge zum Thema Gleichungen, darin Links zu weiteren Aufgaben.
Außerdem hier die Playlist aller Videos zu linearen Gleichungen.
