Einführung in das Horner-Schema

Ganzrationale Funktionen, Mathematik

In diesem Beitrag erkläre ich zuerst, dass man mit dem Horner-Schema einfacher große Funktionswerte berechnen kann. Dann  stelle ich das allgemeine Schema für das Horner-Schema vor. Danach werde ich anhand eines anschaulichen Beispiels erklären, wie man mithilfe des Horner-Schemas die Wertetabelle für eine ganzrationale Funktion höherer Ordnung anlegt. Denn diese braucht man, um deren Graphen zu zeichnen. Außerdem zeige ich, wie das Horner-Schema die Polynomdivision ersetzen kann.

Mit dem Horner-Schema Funktionswerte berechnen:

Wenn man die Funktionswerte einer ganzrationalen Funktion berechnet, erhält man schnell sehr große Zahlen. Das ist nicht nötig, denn es gibt einen Trick. Man klammert x solange aus, bis man nur noch mehrmal mit x multiplizieren und die entsprechenden Koeffizienten zu addieren braucht. Das Horner-Schema stellt das sehr anschaulich dar.

f_0269

Will man den Wert der Funktion für x = x1 berechnen, so kann man folgendermaßen von innen nach außen vorgehen:
– runde Klammer berechnen
– Zwischenergebnis mit x1 multiplizieren und zu a1 addieren
– Ergebnis mit x1 multiplizieren und zu a0 addieren
Im Folgenden Schema zeige ich diese Rechenoperationen:

Allgemeines Schema für das Horner-Schema:

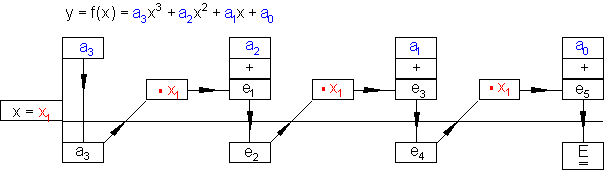
des_036

 

Beispiel Horner-Schema:

y = f (x) = x3 + 3x2 -12x -10
Für x = 2 soll der Wert y = f (2) mit dem Horner – Schema berechnet werden.

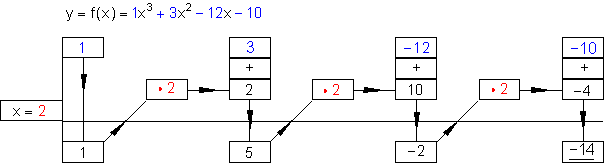
des_037

 

Es gilt also y = f(2) = -14

Dazu kannst du dir das 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.

Beispiel:

Für ein Polynom 3. Grades soll eine Wertetabelle erstellt werden um den Graphen zeichnen zu können.

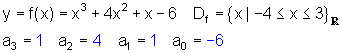
f_0270

 

f_0271

 

Wertetabelle:

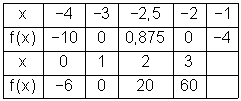
f_0272

 

Mit den Tabellenwerten kann der Graph danach näherungsweise gezeichnet werden.

Sollte sich beim Zeichnen herausstellen, dass noch ein Wert fehlt, so kann man sich diesen trotzdem jederzeit beschaffen.

Der Graph hat bei folgenden x – Werten Nullstellen:
– 3 – 2 und bei 1

Er schneidet die y – Achse bei – 6

mc_048

 

Sollte sich beim Zeichnen herausstellen, dass noch ein Wert fehlt, so kann man sich diesen jederzeit über das Hornerschema beschaffen. z.B. f (0,5)

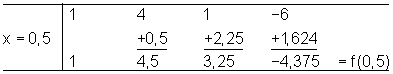
f_0273

 

 

Das Horner-Schema ersetzt Polynomdivision

Dazu kannst du dir auch das Video 📽️ Horner-Schema ersetzt Polynomdivision ansehen.

Wenn es darum geht, Lösungen eines Polynoms zu finden, kann man dazu statt der Polynomdivision auch das Horner-Schema verwenden. Hiermit kann man auf einfache Weise zeigen, dass für das Polynom

x3 – x2 -5x + 6 = 0  x1 = 2 eine Lösung darstelt.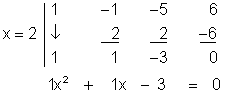
f_1942
Die Zahlen in der dritten Zeile liefern dabei die Koeffizienten des Restpolynoms, wie es auch durch die Polynomdivision erhalten wurde.

Das Horner-Schema liefert also im Schnellverfahren als Abfallprodukt eine Polynomdivision. Ebenfalls lassen sich mit dem Horner-Schema oft auch Lösungen der Polynomgleichung bestimmen. Dazu setzt man in das Schema vorzugsweise Teiler des Absolutgliedes der Polynomgleichung ein.

Beispiel:

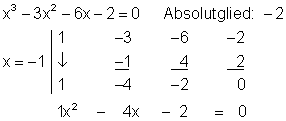
f_1943
Das Restpolynom lässt sich mit der p-q-Formel lösen.

Um weitere Lösungen eines Polynoms zu berechnen, von dem eine Lösung bereits bekannt ist, wird üblicherweise die Polynomdivision verwendet, um das Restpolynom zu erhalten woraus man weitere Lösungen ermitteln kann.

Beispiel:

x3 + x2 – 8x – 8 = 0 sei ein Polynom 3. Grades, von dem die Lösung x1 = -1 bekannt ist.
Folgende Polynomdivision liefert eine quadratische Gleichung als Restpolynom:

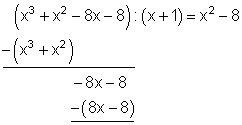
f_1939

 

Restpolynom: x2 – 8 = 0
Die quadratischen Gleichung x2 – 8 = 0 liefert, sofern sie lösbar ist, weitere Lösungen der Polynomgleichung.

Mit dem Horner-Schema lässt sich auf einfache Weise zeigen, das x1 = -1 Lösung der Polynomgleichung ist.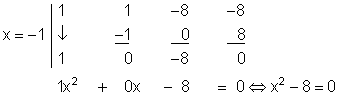
f_1940
Die Zahlen in der dritten Zeile liefern die Koeffizienten des Restpolynoms, wie es auch durch die Polynomdivision erhalten wurde.

Das Horner-Schema liefert also im Schnellverfahren als Abfallprodukt eine Polynomdivision. Ebenfalls lassen sich mit dem Horner-Schema oft auch Lösungen der Polynomgleichung bestimmen. Dazu setzt man in das Schema vorzugsweise Teiler des Absolutgliedes der Polynomgleichung ein.

Fazit:

Hat eine Polynomgleichung eine ganzzahlige Lösung, so lässt diese sich leicht mittels Horner-Schema finden. Das Restpolynom wird dabei gleich mitgeliefert.

Hier findest du Aufgaben für das Horner-Schema: Graphen ganzrationaler Funktionen zeichnen

und Aufgaben ganzrationale Funktionen

und Anwendungsaufgaben Differential und Integralrechnung I.

Hier findest du eine Übersicht über alle Beiträge zum Thema weitere ganzrationale Funktionen, darin auch Links zu weiteren Aufgaben.

Ähnliche Beiträge