In diesem Beitrag führe ich in die Polynomdivision, indem ich sie mit schriftlichen Dividieren vergleiche. Anschließend erkläre ich anhand einiger Beispiele, wie man die Polynomdivision durchführt. Danach zeige, dass man statt der Polynomdivision auch das Horner-Schema einsetzen kann.
Die Polynomdivision funktioniert ähnlich wie das schriftliche Dividieren. Zuerst zeige ich das Prinzip anhand eines
Vergleich zwischen Polynomdivision und schriftlich Dividieren:
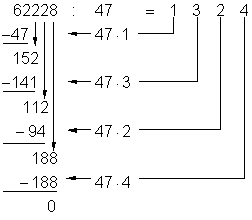
Als erstes dividiert man die Zahl 62, also die ersten zwei Ziffern der zu teilenden Zahl, durch den Teiler (47). Dann multipliziert man das Ergebnis (1) mit dem Teiler 47 und subtrahiert es von der Zahl (62). Mit dem Ergebnis der Subtraktion (152) verfährt man in gleicher Weise. Das führt man so lange durch, bis das Subtraktionsergebnis Null ist. Anschließend kann man eine Probe durchführen.
Bei der Polynomdivision gehen wir ähnlich vor. Deshalb dazu ein
Beispiel für die Polynomdivision
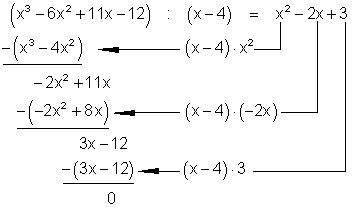
Wieder dividieren wir zuerst den erste Summand des zu teilenden Polynoms ( x3) durch den ersten Summanden des Teilers (x). Dann multipliziert man das Ergebnis (x2) mit dem Teiler (x – 4) und subtrahiert ihn von dem zu teilenden Polynom. Mit dem Ergebnis der Subtraktion ( -2x2 + 11x – 12 ) verfährt man in gleicher Weise. Man führt dieses Verfahren so lange durch, bis das Subtraktionsergebnis Null ist. Als letztes Kann man wieder die Probe durchführen:
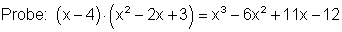
Weil wir unten eine 0 haben, sich also kein Rest ergibt, ist x = 4 eine Nullstelle. Denn wenn wir 4 in (x – 4) einsetzen, ergibt dies 0. Und wenn ein Faktor in einer Multiplikation 0 ist, ist das Ergebnis immer 0.
Mit der Polynomdivieion können wir also Nullstellen berechnen.
Ein ähnliches Beispiel könnt ihr euch in diesem Video ansehen: 📽️Video Polynomdivision
Als nächstes stelle ich ein paar weitere Beispiele vor:
1. Beispiel:
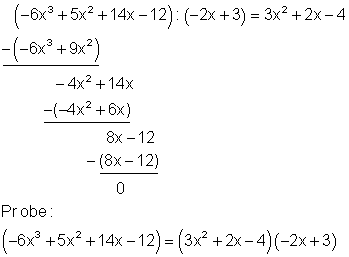
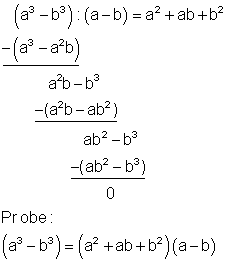
2. Beispiel:
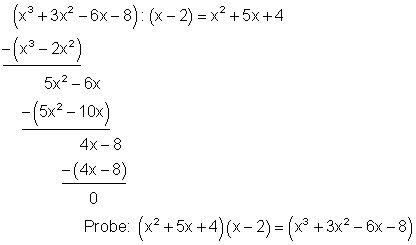
3. Beispiel:
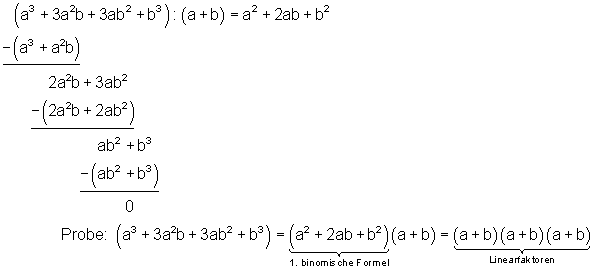
4. Beispiel:
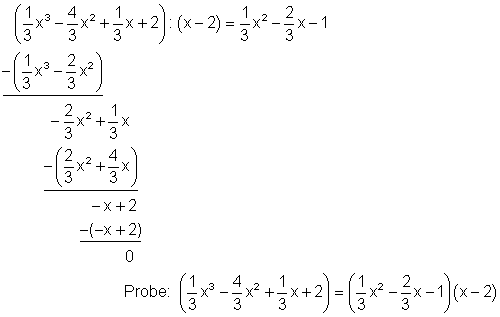
Wie das Beispiel unten zeigt, ist es in manchen Fällen sinnvoll, bei der Schreibweise der Terme eine Lücke zu lassen.
Eine andere Möglichkeit ist, die Lücke mit Null zu füllen.
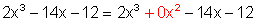
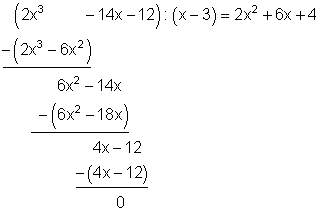
Das folgende Beispiel behandelt die Division mit Rest. Ebenfalls bekannt bei der schriftlichen Division von Zahlen.
5. Beispiel:
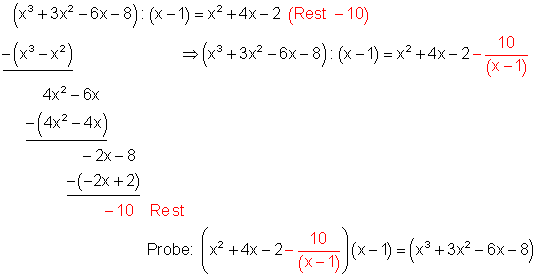
Da gerade Anfänger bei der Durchführung der Polynomdivision immer wieder Fehler machen, ist es wichtig das erhaltene Ergebnis durch eine Proberechnung zu kontrollieren.
Ein Anwendungsbeispiel der Polynomdivision.
Ist von einem Polynom eine Nullstelle bekannt, so kann der Grad des Polynoms um eins reduziert werden.
6. Beispiel:
Rechenregeln zu Potenzen findest du hier
Horner-Schema ersetzt Polynomdivision
Wenn es darum geht, Lösungen eines Polynoms zu finden, kann man dazu statt der Polynomdivision auch das Horner-Schema verwenden.
Dazu könnt ihr euch das Video 📽️ Horner-Schema ersetzt Polynomdivision ansehen.
Hier findest du Aufgaben zur Polynomdivision
Hier findest du eine Übersicht über alle Beiträge zum Thema weitere ganzrationale Funktionen, darin auch Links zu weiteren Aufgaben.
