Hier findest du die Lösungen der Aufgaben zum Funktionsgleichungen bestimmen. Entweder ist ein Punkt und die Steigung gegeben oder zwei Punkte.
Teil 1 : Die Steigung und ein Punkt sind vorgegeben.
Eine Gerade hat jeweils die Steigung a1 und verläuft durch den Punkt P. Bestimmen Sie die Funktionsgleichung f(x), die Achsenschnittpunkte und zeichnen Sie den Graphen.
Im Beitrag mit den Trainingsaufgaben Funktionsgleichungen aufstellen habe ich ausführliche Tipps zum Vorgehen gegeben.
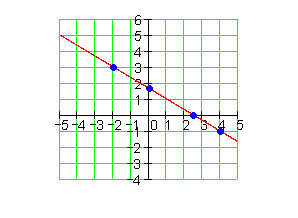
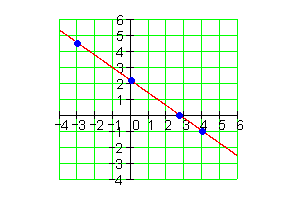
Hier noch einmal in Kurzform: Die Steigung a1 kann man direkt als Multiplikation mit x einfügen. Wenn wir z. B. in der ersten Aufgabe den Punkt (2 | – 2) haben, dann steht die 2 ja für den x-Wert, die -2 für den y-Wert. Deshalb kann man in der Gleichung die 2 für x einsetzen. Die setzt man für y, also für das Ergebnis der Funktionsgleichung ein. Dann kann man a0 ganz einfach ausrechnen.
1.
a_1 = \frac{1}{2} \quad P(2 | -2)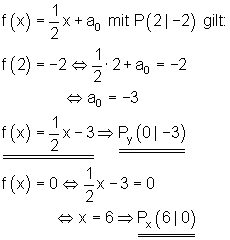
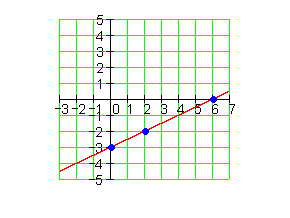
2.
a_1= \frac{3}{4} \quad P (-1 | 3)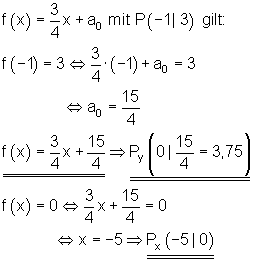
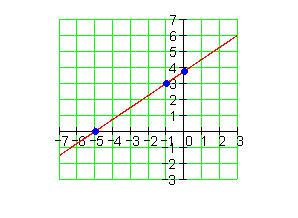
3.
a_1 = 2 \quad P (3 | -1)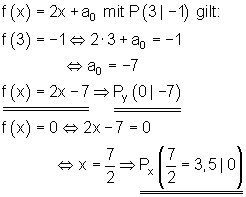
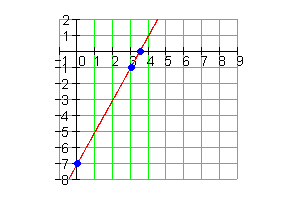
4.
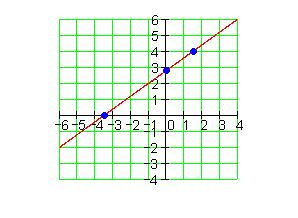
a_1 = \frac{4}{5} \quad P(\frac{3}{2} | 4)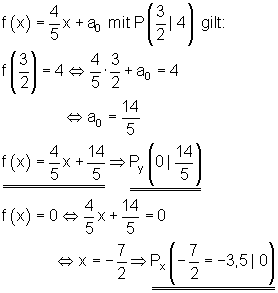
Teil 2 : Die Steigung und ein Punkt sind vorgegeben.
Eine Gerade verläuft durch die Punkte P1 und P2. Bestimmen Sie die Funktionsgleichung f(x), die Achsenschnittpunkte und zeichnen Sie den Graphen.
Im Beitrag mit den Trainingsaufgaben Funktionsgleichungen aufstellen habe ich ausführliche Tipps zum Vorgehen gegeben.
Hier noch einmal in Kurzform: Man subtrahiert die y-Werte der beiden Punkte, z. B. in der 5. Aufgabe 4-1= 3. Und deren x-Werte, z. B. 5 – 2 = 3. Dadurch erhält man die Steigung. Danach kann man wieder vorgehen wie in den vorherigen Aufgaben.
5.
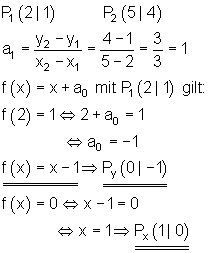
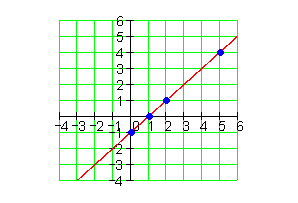
6.
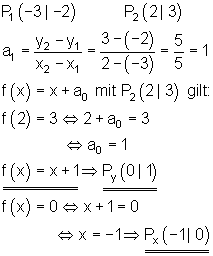
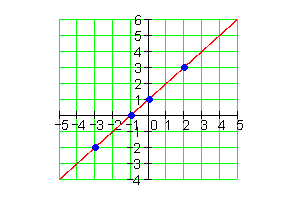
7.
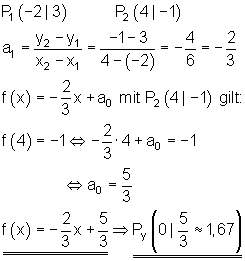
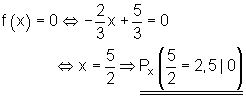
8.
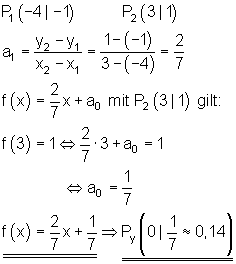
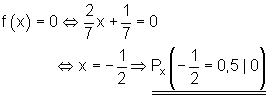
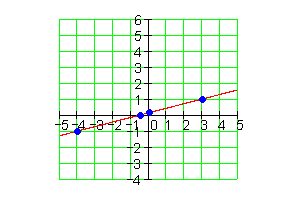
9.
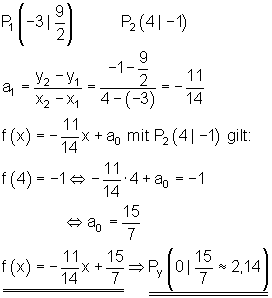
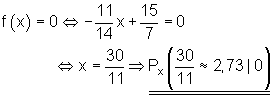
10.
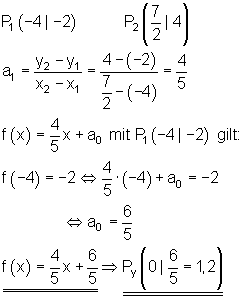
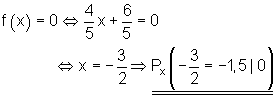
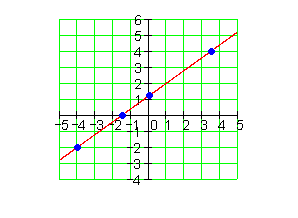
Hier findest du die Trainingsaufgaben Funktionsgleichungen aufstellen.
Und hier habe ich die Vorgehensweise erklärt: Einführung lineare Funktionen.
Hier findest du eine Übersicht über weitere Beiträge zu linearen Funktionen.