In diesem Beitrag zeige ich, wie man lineare Funktionen als Kostenfunktion im Alltag einsetzen kann. Anhand vieler Beispiele und Übungen erkläre ich, wie man lineare Funktionsgleichungen aufstellt, die Achsenschnittpunkte bestimmt und den Funktionsgraphen zeichnet.
- Kostenfunktion
- Beispiele: Aufstellen linearer Funktionsgleichungen
- Definition Ganzrationale Funktion n-ten Grades:
- Beispiele für Funktionsgleichungen linearer Funktionen
- Übung 1:
- Definition: Achsenschnittpunkte linearer Funktionen
- Die Steigung linearer Funktionen
- Funktionsgraphen zeichnen
- Begriffe und Darstellungsarten
- Lösungen der Übungen
Aus der Sekundarstufe I sind dir die Graphen linearer Funktionen als Geraden bekannt und deren Funktionsgleichungen als Geradengleichungen. Proportionale Zusammenhänge lassen sich durch Geraden darstellen.
Beispiel 1 lineare Funktion:
Am Fischstand auf dem Wochenmarkt kosten 100 g Schillerlocken 4,50 €.
Frau Barsch möchte 300 g kaufen.
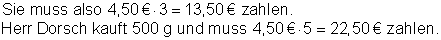
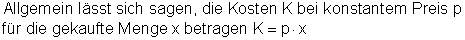
Die Kosten K sind also von der Menge x abhängig und somit eine Funktion von x.
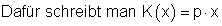
Begriff: Kostenfunktion:
K(x) wird auch Kostenfunktion genannt.
Für den Kauf von Schillerlocken lautet die Kostenfunktion K(x) = 4,50 x, wobei 4,50 der Preis pro Mengeneinheit in € und x die Anzahl der Mengeneinheiten in Vielfachen von 100 g ist.
Ersetzt man K(x) durch y, dann entsteht die bekannte Gleichung y = 4,50 x.
Im Koordinatenystem ist das eine Gerade durch den Nullpunkt.
Beispiel 2 lineare Funktion:
Sven hat einen Handyvertrag mit monatlichen Grundgebühren von 20 €.
Für jede Minute die er telefoniert fallen 0,2 € an.
a) Welche Kosten entstehen monatlich, wenn Sven 30 min, 60 min, 90 min, 120 min telefoniert?
Stelle die Werte in einer Wertetabelle dar.
Lösung: Die Kosten setzen sich additiv aus einem festen (20 €) und einem variablen Anteil (0,2 x) zusammen, wobei x die Anzahl der telefonierten Minuten ist.
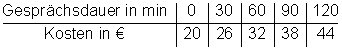
b) Zeichne den Graphen in ein geeignetes Koordinatensystem.
Lösung: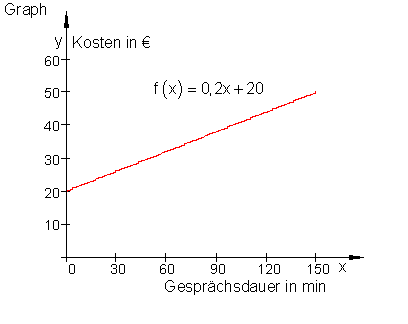
c) Wie lautet die Funktionsgleichung für die Kostenrechnung?
Lösung: x ist die unabhängige Variable für die Gesprächsdauer in Minuten.
y = f(x) ist die abhängige Variable für die monatlichen Gesamtkosten in €.
Bei folgender Rechnung werden die Einheiten min und € weggelassen.Ansatz für die Funktionsgleichung:
Beispiele: Aufstellen linearer Funktionsgleichungen
Ein Abwasserschacht enthält 1000 Liter Wasser. Jeden Tag kommen 100 Liter dazu.

Thorsten verdient jeden Monat 1300 € netto. Funktionsgleichung für den Nettoverdienst in €:![]()
Ein Tank enthält 4000 Liter Diesel. Jede Woche verbraucht ein Motor 500 Liter.![]()
Soll für einen proportionalen Zusammenhang die Funktionsgleichung aufgestellt werden, ist zuerst zu überlegen:
- Gibt es einen Anfangswert a0?
- Wie groß ist die Änderungsrate (z.B. Änderung pro Tag, Minute, Stück oder Gewicht).
- Ist die Änderungsrate positiv oder Negativ (positiv = Zunahme, negativ = Abnahme).
Wir kennen die Funktionsgleichung der Geraden in der Form:![]()
Da Geradengleichungen zur Familie der ganzrationalen Funktionen gehören, die ein zentrales Thema der Oberstufenmathematik sind, soll deren Darstellungsart von Anfang an auf diese übertragen werden.
Wie man aus einer Textaufgabe eine lineare Funktion aufstellt, dazu kannst du dir dieses Video ansehen:
Definition Ganzrationale Funktion n-ten Grades:
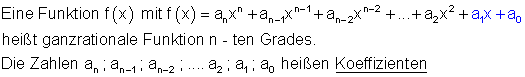
Da die beiden letzten Summanden a1x + a0 zum Funktionsterm der Geradengleichung gehören, folgt die Definition:
Ganzrationale Funktion 1. Grades
![]()
heißt ganzrationale Funktion 1. Grades oder lineare Funktion.
Der Grad der Funktion wird durch den höchsten Exponenten von x
(hier also 1, denn x = x1) bestimmt.
Der Koeffizient a1 steht für m und a0 steht für b oder n.
Die Bezeichnung „lineare Funktion“ rührt daher, dass der Graph einer linearen Funktion im rechtwinkligem Koordinatensystem eine Gerade darstellt.
Merke: Der Graph einer linearen Funktion stellt eine Gerade dar.
Beispiele für Funktionsgleichungen linearer Funktionen:
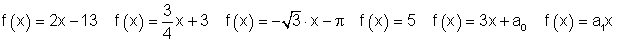
Übung 1 lineare Funktion:
Stelle für die ganzzahligen Werte von D eine Wertetabelle auf und zeichne den Graphen.![]()
Bestimme die Wertemenge W für die Definitionsmenge D.
In welchen Punkten schneidet der Graph die Koordinatenachsen?
Lösung unten
Definition: Achsenschnittpunkte linearer Funktionen
Achsenschnittpunkte sind die Punkte, in denen der Graph die Koordinatenachsen schneidet.
Diese Werte lassen sich mehr oder weniger genau aus dem Graphen ablesen.
Oft besteht auch die Möglichkeit, der Wertetabelle diese Daten zu entnehmen.
Nun soll es darum gehen, diese Werte durch Rechnung, ohne Wertetabelle und Graph zu nutzen zu bestimmen.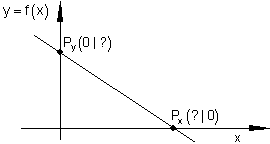
Schnittpunkt mit der y-Achse (Ordinate) Py:

Merke:
Der Schnittpunkt mit der y-Achse kann für alle lineare Funktionen der Form
![]()
Schnittpunkt mit der x-Achse (Abszisse) Px:
Die y-Werte (Funktionswerte) aller Punkte, die auf der x-Achse liegen haben den Wert 0.![]()
Beispiel:
Bestimme von folgender Funktion die Achsenabschnitte und zeichne den Graphen.
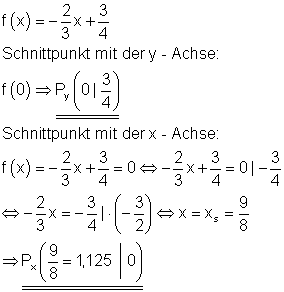
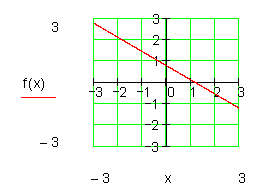
Die x-Koordinate des Schnittpunktes mit der x-Achse wird auch Nullstelle genannt.
Denn für diesen x-Wert (an dieser Stelle x) ist der Funktionswert Null.
Übung 2:
Berechne die Achsenschnittpunkte und zeichne den Graphen für![]()
Kontrolliere die Nullstelle durch Einsetzen in f(x).
Lösung unten
Nullstellenfinder
Interaktiv: Man kann eine Gleichung eingeben und das JavaScript bestimmt Nullstellen von Polynomen bis 9. Grades und zeichnet den Funktionsgraphen.
Die Steigung linearer Funktionen
Die meisten Schienen oder Straßenfahrzeuge können nur geringe Steigungen überwinden. Im Gebirge setzt man daher Zahnradbahnen oder Seilbahnen ein, diese eignen sich auch für steile Strecken.
Das Verkehrsschild „12% Steigung“ bedeutet:Auf 100 m horizontaler Strecke steigt die Straße um 12 m an. Es wird ein Höhenunterschied von 12 m überwunden.
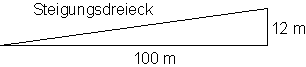
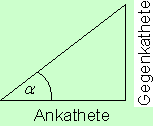
Definition Steigung einer Geraden:
Das Verhältnis zwischen Höhenunterschied und horizontaler Strecke wird Steigung genannt.

Das Steigungsdreieck ist ein rechtwinkliges Dreieck für das gilt:
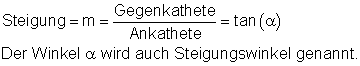
In der Grafik unten ist eine Ursprungsgerade, durch die Punkte P1 und P2 abgebildet.
Die Steigung der Geraden soll mit Hilfe der Koordinaten von P1 und P2 ermittelt werden.
Die Längen von Gegenkathete und Ankathete sind durch die Koordinatendifferenzen der beiden Punkte festgelegt.
Für die Differenzen schreibt man:
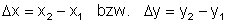
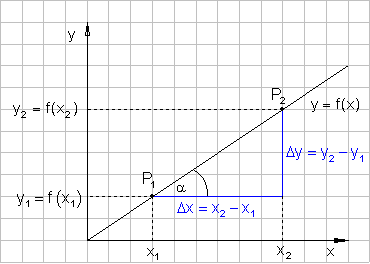
Aus dem Steigungsdreieck lässt sich die Steigung der Geraden ablesen:
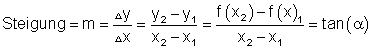
Die Steigung einer Geraden im Koordinatensystem ist das Verhältnis von Gegenkathete zur Ankathete eines beliebigen rechtwinkligen Dreiecks (Steigungsdreieck), dessen Hypotenuse Teil des Funktionsgraphen ist.
Die Vermutung liegt nahe, dass der Koeffizient a1 der Geradengleichung
f(x) = a1x + a0 für die Steigung der Geraden verantwortlich ist.
Das soll nun bewiesen werden.
Beweise:
Behauptung:
Die Steigung m entspricht dem Koeffizienten a1 der Geradengleichung:
f(x) = a1x + a0
Beweis:

Satz:

Sind also zwei Punkte einer Geraden durch ihre Koordinaten gegeben, so kann man:
1. Die Gerade zeichnen indem man die beiden Punkte miteinander verbindet und die so entstandene Gerade über die Punkte hinaus verlängert.
2. Die Steigung der Geraden mit Hilfe des Steigungsdreiecks errechnen.
Beispiel:
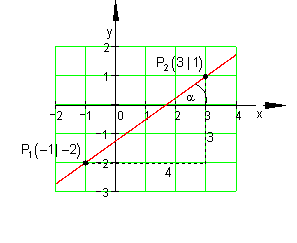
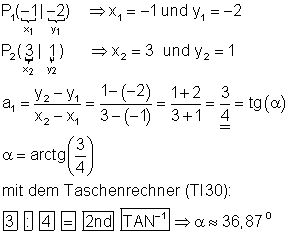
Dazu kannst du dir auch dieses 📽️Video Lineare Funktion aus 2 Punkten erstellen ansehen:
Funktionsgraphen zeichnen
Der Graph einer linearen Funktion ist immer eine Gerade. Um eine Gerade zeichnen zu können, sind zwei Punkte nötig. Ist die Funktionsgleichung bekannt, kennen wir auch den Schnittpunkt mit der y -Achse Py. Den zweiten Punkt erhalten wir durch die Steigung (Steigungsdreieck).
Beispiel:

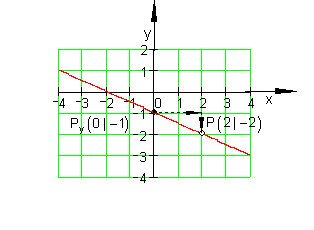
Um von einem bestimmten Punkt der Geraden über das Steigungsdreieck zu einem zweiten Punkt zu gelangen, kann man sich in Kurzform folgendes merken:
Merke:
Nennereinheiten nach rechts, Zählereinheiten in Abhängigkeit vom Vorzeichen nach oben oder nach unten.
Dabei gilt: für + nach oben, für – nach unten.
Liegen die beiden Punkte zu nahe beieinander, dann kann das Verfahren mehrfach angewendet werden. Auch wenn der Steigungsfaktor a1 eine ganze Zahl ist, lässt sich der zweite Punkt auf diese Weise bestimmen, denn jede Zahl lässt sich in einen Bruch verwandeln.
Beispiel:

Geht man in vier Schritten vor, so liegen beide Punkte weit genug auseinander um eine saubere Gerade zeichnen zu können.Von P gehen wir vier mal jeweils einen Schritt nach rechts und einen Schritt nach unten und erhalten den Punkt P1. Vier Schritte nach rechts und 4 Schritte nach unten führt auf das gleiche Ergebnis.
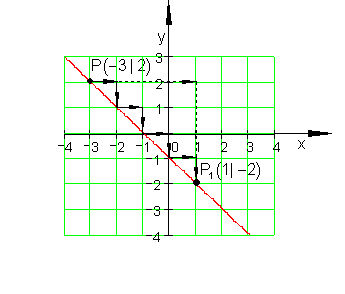
Beispiel:

Dazu gibt es hier Trainingsaufgaben mit Lösungen
Geraden erkennen
Interativ: Finde zu dem angegebenen Graphen die entsprechende Funktionsgleichung. Nach dem Durchlauf von 10 Aufgaben erfolgt eine Benotung
Begriffe und Darstellungsarten
Der Graph einer Funktion f(x) wird auch Schaubild Kf genannt.
Im rechtwinkligen Koordinatensystem hat jeder Punkt P eine x- und eine y-Koordinate P ( x | y ).
Die x-Koordinate entspricht der unabhängigen Variablen x der Funktion f(x).
Die y-Koordinate entspricht dem jeweiligen Funktionswert von f(x).
Deshalb verwendet man oft die Schreibweise y = f(x).
Speziell bei linearen Funktionen sind auch folgende Schreibweisen üblich:
Übung 3:
K_f ist das Schaubild der linearen Funktion f mit f(x) = 1,5x - 2, \qquad x \in \mathbb{R}
Statt Schaubild einer Funktion K_f sagt man auch Graph einer Funktion f .
a) Liegt der Punkt P(2,5 \mid 1,75) auf der Geraden K_f ?
b) Die Punkte A(x_A \mid 4) und B(-2 \mid y_B) liegen auf K_f . Bestimme x_A und y_B .
c) Berechne die Nullstelle von f(x) .
d) Für welche x-Werte gilt f(x) > 0 ?
e) Bestimme den Wertebereich von f(x) , wenn D = \mathbb{R}_+^* gewählt wird.
f) Der Graph g entsteht durch Verschiebung von K_f in y-Richtung und verläuft durch N( 4 \mid 0 )
Lösung unten
Beispiel:
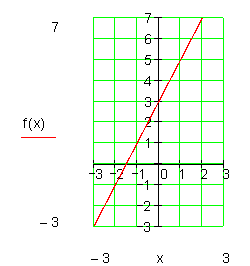
Der Schnellimbiss „MC- Pommes“ benötigt für die Fritteusen täglich 19 kg frisches Fett. Momentan sind noch 250 kg im Lager vorhanden.
a) Stelle die Funktionsgleichung auf und zeichne den Graphen in ein geeignetes Koordinatensystem.
Lösung: Die unabhängige Variable x steht für die Zeit in Tagen.
Die abhängige Variable f(x) steht für die verbleibende Menge Fett in kg.
Der Anfangswert beträgt 250 kg.
Die Änderungsrate ist negativ und beträgt 19kg/Tag.
Da ein linearer Zusammenhang besteht gilt:
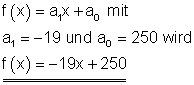
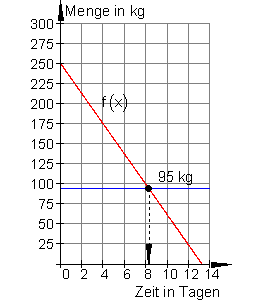
b) Bei einem Lagerbestand von 95 kg soll der Filialleiter nachbestellen. Nach wie viel Tagen muss die Bestellung erfolgen?
Lösung: Da bei 95 kg nachbestellt werden soll, gilt der Ansatz: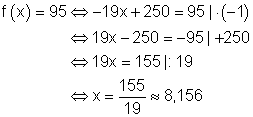
Die Bestellung muss in etwa 8 Tagen erfolgen.
c) Wie lange reicht das Fett, wenn nicht nachbestellt wird?
Lösung: Zu bestimmen ist der Schnittpunkt des Graphen mit der y-Achse:
Das Fett reicht noch etwa 13 Tage.
Lösungen der Übungen zu linearen Funktionen
Übung 1:
Stelle für die ganzzahligen Werte von D eine Wertetabelle auf und zeichne den Graphen.![]()
Bestimme die Wertemenge W für die Definitionsmenge D.
In welchen Punkten schneidet der Graph die Koordinatenachsen?
Lösung: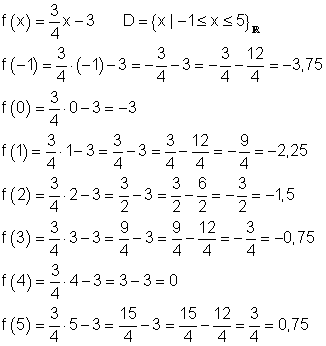
![]()
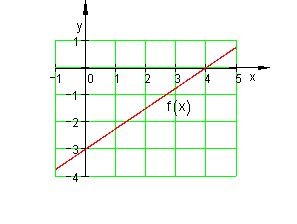
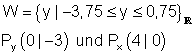
Übung 2 lineare Funktion:
Berechne die Achsenschnittpunkte und zeichne den Graphen für![]()
Kontrolliere die Nullstelle durch Einsetzen in f(x).
Lösung:
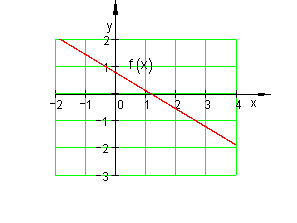
Probe:![]()
Übung 3 lineare Funktion:
K_f ist das Schaubild der linearen Funktion f mit f(x) = 1,5x - 2, \qquad x \in \mathbb{R}
Statt Schaubild einer Funktion K_f sagt man auch Graph einer Funktion f .
a) Liegt der Punkt P(2,5 \mid 1,75) auf der Geraden K_f ?
Lösung: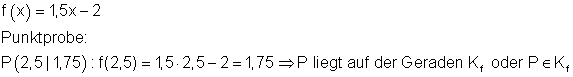
b) Die Punkte A(x_A \mid 4) und B(-2 \mid y_B) liegen auf K_f . Bestimme x_A und y_B .
Lösung:
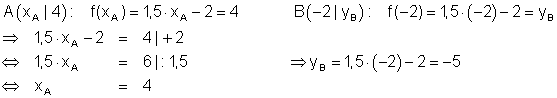
c) Berechne die Nullstelle von f(x).
Lösung: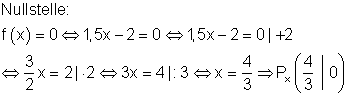
d) Für welche x-Werte gilt f(x) > 0?
Lösung: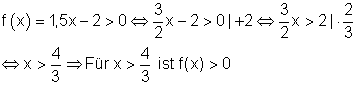
e) Bestimmee den Wertebereich von f(x) , wenn D = \mathbb{R}_+^* gewählt wird.
Lösung:
f) Der Graph g entsteht durch Verschiebung von Kf in y-Richtung und verläuft durch N( 4 | 0 )
Lösung: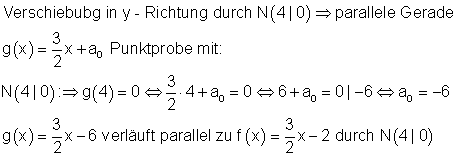
Im nächsten Beitrag erkläre ich anhand von Beispielen aus der Praxis, wie man vorgehen sollte, wenn man eine Funktionsgleichung aufstellen will.
Hier findest du Aufgaben Lineare Funktionen Aufgaben I zu einer Geraden
und Aufgaben Lineare Funktionen Aufgaben II zu einer Geraden
und Aufgaben Lineare Funktionen Aufgaben III zu einer Geraden.
Hier findest du eine Übersicht über alle Beiträge zum Thema Lineare Funktionen, darin auch Links zu weiteren Aufgaben.


