Hier findest du die Lösungen der Aufgaben zu linearen Funktionen und Tipps, wie man sie löst
Die Aufgabenstellung ist bei allen Aufgaben gleich: Zeichne jeweils den Graphen der Geraden mit nebenstehender Funktionsgleichung und berechne danach die Achsenschnittpunkte! Benutze für die Zeichnung das Steigungsdreieck!
1. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
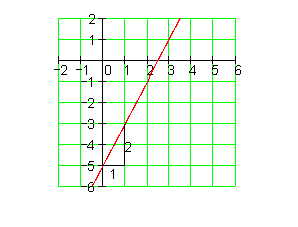
Die Vorgehensweise ist ebenfalls immer gleich:
Lies aus der Funktionsgleichung die y-Koordinate von Py ab und bestimme den Punkt Py. Zeichne danach den Punkt Py ins Koordinatensystem. Lies dann den Steigungsfaktor aus der Funktionsgleichung ab und bilde daraus einen Bruch. Beginnend von Py zeichne nun das Steigungsdreieck ein. Dabei ist der Nenner der x Abschnitt und der Zähler der y-Abschnitt. Durch Verlängerung der Hypotenuse nach beiden Seiten, entsteht dadurch die Gerade im Koordinatensystem. Den Schnittpunkt mit der x-Achse findet man, indem die Funktionsgleichung Null gesetzt und nach x aufgelöst wird. Der so gefundene x-Wert ist die Nullstelle, an der der Graph die x-Achse schneidet. Zur Kontrolle kann man das Ergebnis mit dem Graphen vergleichen.
2. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
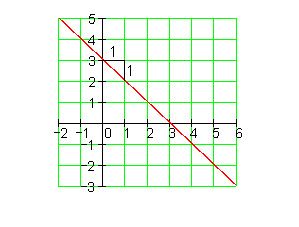
3. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
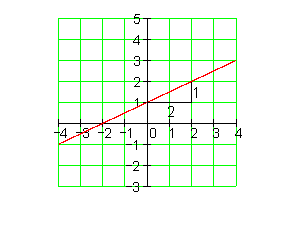
4. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
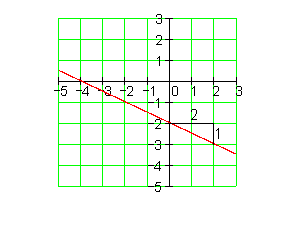
5. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
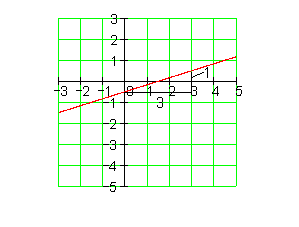
6. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
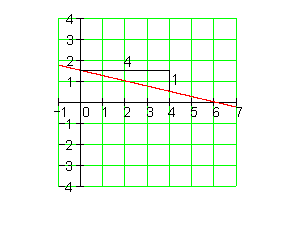
7. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
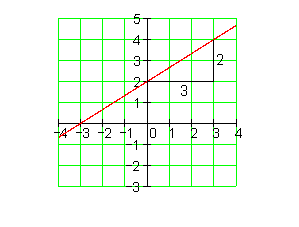
8. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
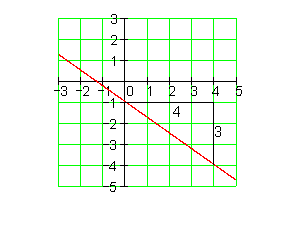
9. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
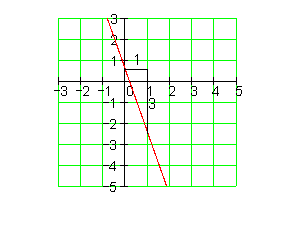
10. Zeichne den Graphen und berechne danach die Achsenschnittpunkte
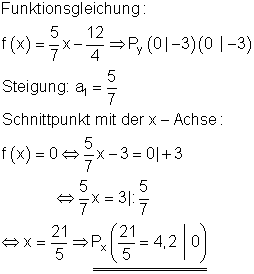
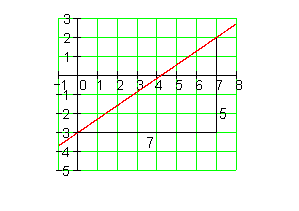
Hier findest du die Aufgaben.
Und hier die Theorie hierzu: Einführung lineare Funktionen.
Hier findest du eine Übersicht über weitere Beiträge zu linearen Funktionen.
