Aufgaben zur Polynomdivision

Bevor ich hier die Aufgaben zur Polynomdivision stelle, zeige ich Hilfestellungen:

Anhand eines Beispiels zeige ich noch einmal die Vorgehensweise:

Tipps zur Vorgehensweise:

Zuerst dividiert man den ersten Summanden des zu teilenden Polynoms ( x³ ) durch den ersten Summanden des Teilers ( x ). Danach multipliziert man das Ergebnis ( x² )  mit dem Teiler ( x + 3 ) und subtrahiert ihn von dem zu teilenden Polynom. Mit dem Ergebnis der Subtraktion ( -x² – 5x – 6 ) verfährt man ebenso. Man führt dieses Verfahren so lange durch, bis das Subtraktionsergebnis Null ist. Danach macht man die Probe durch ausmultiplizieren.

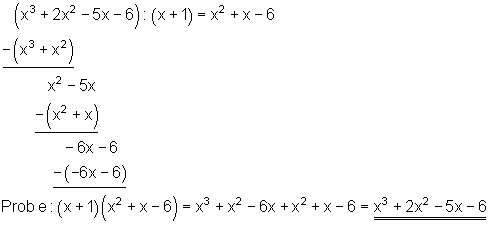
Dazu könnt ihr euch das 📽️Video Polynomdivision ansehen.

1. Führe folgende Polynomdivisionen durch und mache die Probe.

a) (x³ + 2x² – 5x – 6) : (x + 3)
b) (2x³ – 14x – 12) : ( x + 2)
c) (3x³ – 15x² – 51x + 63) : (x + 3)
d) katex is not defined
e) katex is not defined
f) katex is not defined
g) katex is not defined
h)

i)

j)

k)

l)

m)

n)

2. Führe die Polynomdivision durch:

a) (x³ – 3x² – 6x + 8) : (x + 1)
b) (2x³ – x² – 8x + 4) : (x² – 4)
c) (2x³ – 3x + 1) : (2x – 1)
d) (x³ – tx² – 2x + 2t) : (x² – 2)

3. Führe die Polynomdivision durch:

a) (8x⁵ – 6x⁷ + 2x) : 2x²
b) (9a⁵b³ – 12a³b⁵ ) : 3a³b³
c) (6a⁶ + a⁴b + 25b³ ) : (3a² + 5b)
d) (15a⁹ – 8a⁶b + 8b³ ) : (3a³ + 2b)
e) (14a⁴ – a³ + 5a² – 3a + 1) : (7a² – 4a + 1)
f) ( a⁵ + a⁴ – 8a³ + 26a² – 29a + 21) : (a² – 2a + 3)
g) (a³ – 2a²b + 2ab² – b³ ) : (a – b)
h) (a³ + 2a²b + 2ab² + b³ ) : (a + b)

4. Führe die Polynomdivision durch:

a)

b)

c)

d)

Hier findest du die ausführlichen Lösungen mit Tipps als Starthilfe.

Und hier die dazugehörige Theorie: Polynomdivision.

Hier eine Übersicht über weitere ganzrationale Funktionen, darin Links zu weiteren Aufgaben.