Hier findest du die Lösungen der Aufgaben zur Polynomdivision mit komplettem Lösungsweg.
1. Führe die Polynomdivision durch!
a) Ausführliche Lösung
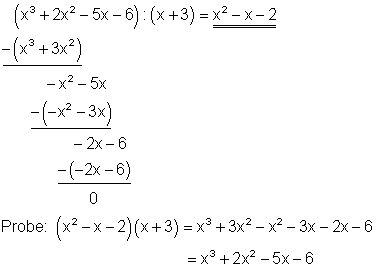
Dazu könnt ihr euch das 📽️Video Polynomdivision ansehen.
1. b) Ausführliche Lösung
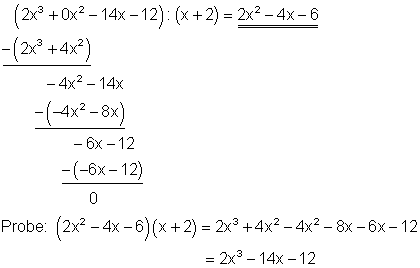
Starthilfe:
Da der Dividend keinen Summanden mit x2 enthält, setzt man zuerst an entsprechender Stelle 0x2 ein. Das macht die Rechnung übersichtlicher. Den ersten Summanden des zu teilenden Polynoms (2x3 ) dividiert man danach durch den ersten Summanden des Teilers ( x ). Das Ergebnis ( 2x2 ) multipliziert man mit dem Teiler ( x + 2 ) und subtrahiert ihn von dem zu teilenden Polynom. Mit dem Ergebnis der Subtraktion ( -4x2 – 14x – 12 ) verfährt man in gleicher Weise. Man führt dieses Verfahren so lange durch, bis das Subtraktionsergebnis Null ist. Danach macht man die Probe durch ausmultiplizieren.
1. c) Ausführliche Lösung
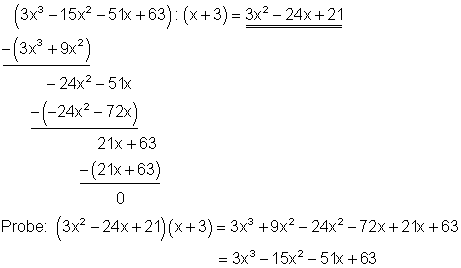
Starthilfe:
Zuerst dividiert man den ersten Summanden des zu teilenden Polynoms (3x3 ) durch den ersten Summanden des Teilers ( x ). Das Ergebnis ( 3x2 ) multipliziert man danach mit dem Teiler ( x + 3) und subtrahiert ihn von dem zu teilenden Polynom. Mit dem Ergebnis der Subtraktion ( -24x2 – 51x + 63 ) verfährt man in gleicher Weise. Man führt dieses Verfahren so lange durch, bis das Subtraktionsergebnis Null ist. Danach macht man die Probe durch ausmultiplizieren.
1. d) Ausführliche Lösung
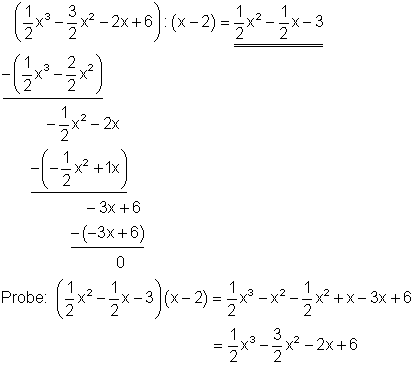
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
1. e) Ausführliche Lösung
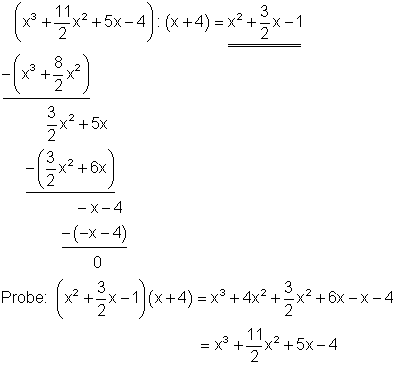
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
1. f) Ausführliche Lösung
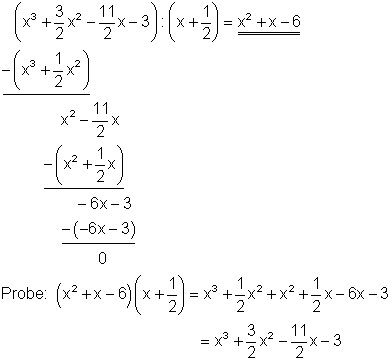
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
1. g) Ausführliche Lösung
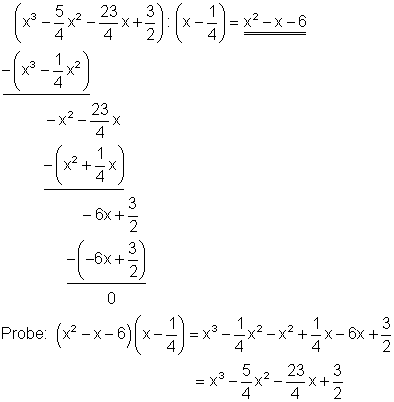
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
1.h) Ausführliche Lösung
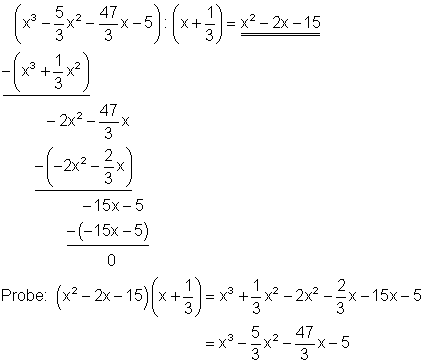
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
1.i) Ausführliche Lösung
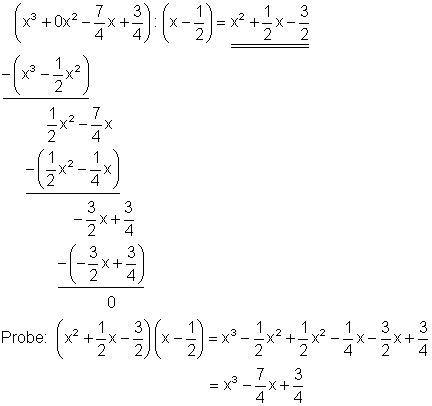
Starthilfe:
Da der Dividend keinen Summanden mit x2 enthält, setzt man zuerst an entsprechender Stelle 0x2 ein. Das macht die Rechnung übersichtlicher. Danach dividiert man den ersten Summanden des zu teilenden Polynoms ( x3 ) durch den ersten Summanden des Teilers ( x ). Das Ergebnis ( x2 ) multipliziert man anschließend mit dem Teiler ( x – 1/2 ) und subtrahiert ihn von dem zu teilenden Polynom. Mit dem Ergebnis der Subtraktion ( 1/2x2 – 7/4x + 3/4 ) verfährt man in gleicher Weise. Man führt dieses Verfahren so lange durch, bis das Subtraktionsergebnis Null ist. Danach macht man die Probe durch ausmultiplizieren.
1. j) Ausführliche Lösung
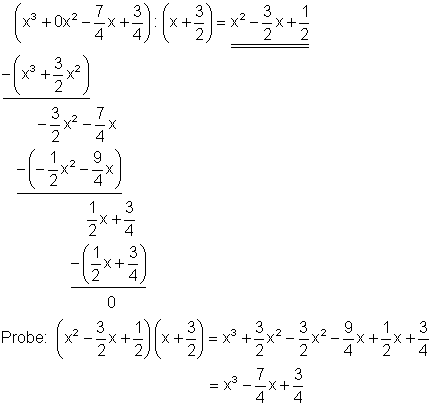
Starthilfe: Man verfährt hier ebenso wie unter 1b und 1i erklärt.
1. k) Ausführliche Lösung
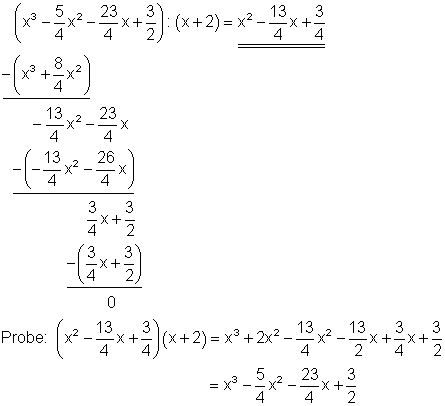
Starthilfe: Man verfährt hier ebenso wie unter 1b und 1i erklärt.
1. l) Ausführliche Lösung
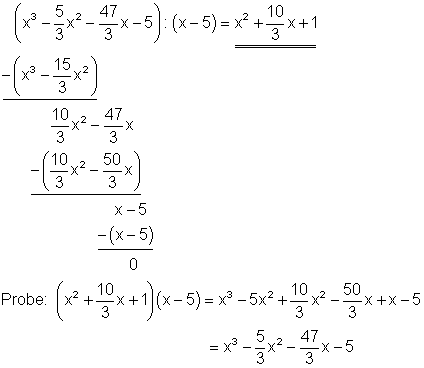
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
1. m) Ausführliche Lösung
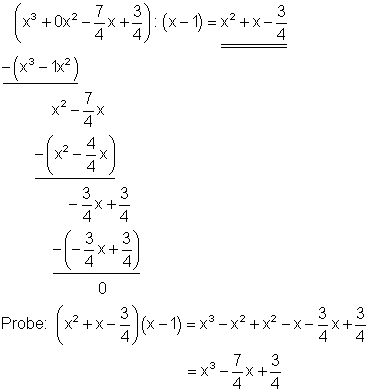
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
1. n) Ausführliche Lösung
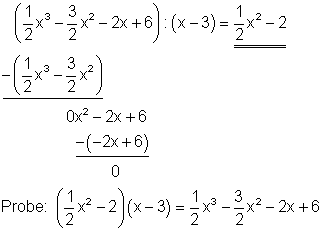
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
2. Führe die Polynomdivision durch!
a) Ausführliche Lösung
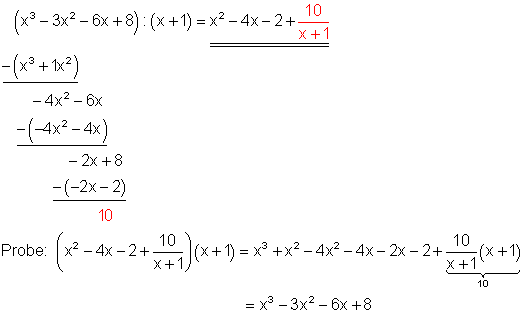
Starthilfe:
Zuerst dividiert man den ersten Summanden des zu teilenden Polynoms ( x3 ) durch den ersten Summanden des Teilers ( x ). Das Ergebnis ( x2 ) multipliziert man danach mit dem Teiler ( x + 1 ) und subtrahiert ihn von dem zu teilenden Polynom. Mit dem Ergebnis der Subtraktion ( -4x2 – 6x + 8 ) verfährt man in gleicher Weise. Die Division geht jedoch nicht glatt auf, es bleibt ein Rest von 10. Man fügt das Restglied 10/( x + 1 ) deshalb dem Divisionsergebnis hinzu. Danach macht man die Probe durch ausmultiplizieren.
2.b) Ausführliche Lösung
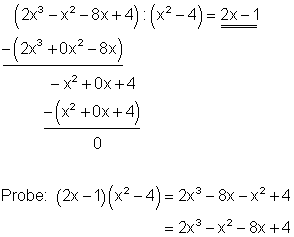
Starthilfe:
Zuerst dividiert man den ersten Summanden des zu teilenden Polynoms ( 2x3 ) durch den ersten Summanden des Teilers ( x2 ). Das Ergebnis ( 2x ) multipliziert man danach mit dem Teiler ( x2 – 4 ) und subtrahiert ihn von dem zu teilenden Polynom. Mit dem Ergebnis der Subtraktion ( -x2 + 0x + 4 ) verfährt anschließend man in gleicher Weise. Man führt dieses Verfahren so lange durch, bis das Subtraktionsergebnis Null ist. Danach macht man die Probe durch ausmultiplizieren. Es ist vorteilhaft, die bei der Rechnung entstehenden Lücken mit 0 aufzufüllen, damit gleiche Potenzen übereinanderstehen.
2.c) Ausführliche Lösung
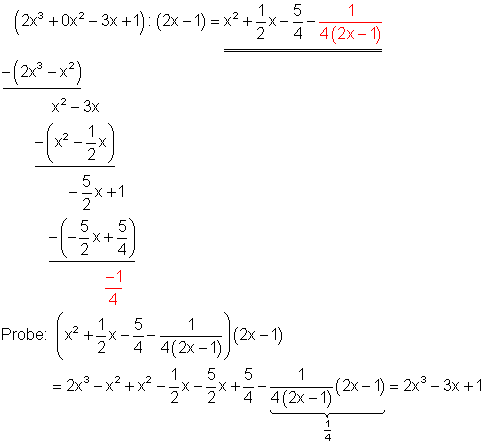
Starthilfe:
Zuerst dividiert man den ersten Summanden des zu teilenden Polynoms ( 2x3 ) durch den ersten Summanden des Teilers ( 2x ) . Das Ergebnis multipliziert man danach ( x2 ) wird mit dem Teiler ( 2x – 1 ) und subtrahiert ihn von dem zu teilenden Polynom. Mit dem Ergebnis der Subtraktion ( x2 – 3x + 1 ) verfährt anschließend man in gleicher Weise. Die Division geht nicht glatt auf, es bleibt ein Rest von -1/4. Das Restglied -1/[4( 2x – 1 )] fügt man deshalb dem Divisionsergebnis hinzu. Danach macht man die Probe durch ausmultiplizieren.
2. d) Ausführliche Lösung
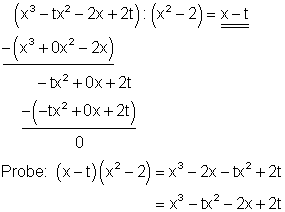
Starthilfe:
Zuerst dividiert man den ersten Summanden des zu teilenden Polynoms ( x3 ) durch den ersten Summanden des Teilers ( x2 ). Das Ergebnis ( x ) multipliziert man danach mit dem Teiler ( x2 – 2 ) und subtrahiert ihn von dem zu teilenden Polynom. Mit dem Ergebnis der Subtraktion ( -tx2 + 0x + 2t ) verfährt man anschließend in gleicher Weise. Man führt dieses Verfahren so lange durch, bis das Subtraktionsergebnis Null ist. Danach macht man die Probe durch ausmultiplizieren. Es ist vorteilhaft, die bei der Rechnung entstehenden Lücken mit 0 aufzufüllen, damit gleiche Potenzen übereinanderstehen. Der Parameter t ist dabei Platzhalter für eine beliebige Zahl ungleich Null.
3. Führe die Polynomdivision durch!
a) Ausführliche Lösung
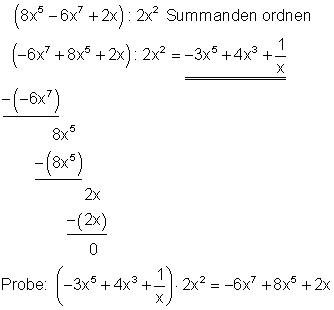
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
3. b) Ausführliche Lösung
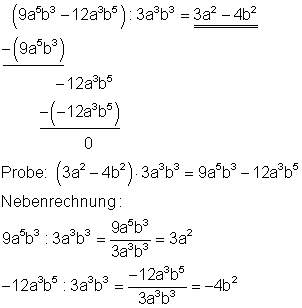
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
3. c) Ausführliche Lösung
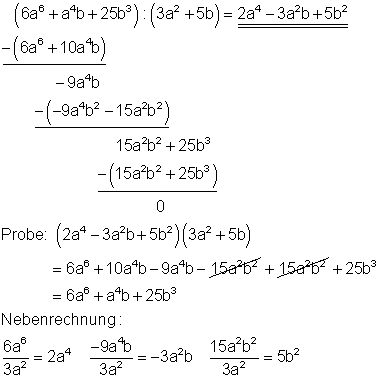
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
3. d) Ausführliche Lösung
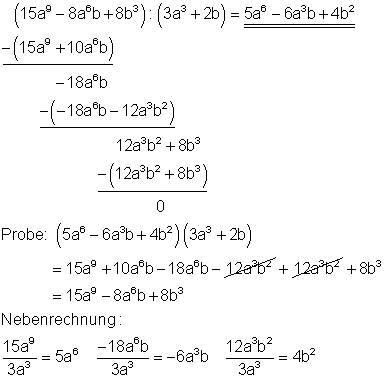
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
3. e) Ausführliche Lösung
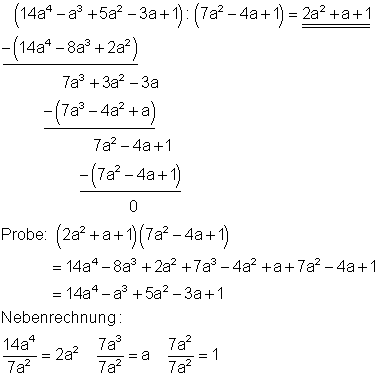
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
3. f) Ausführliche Lösung
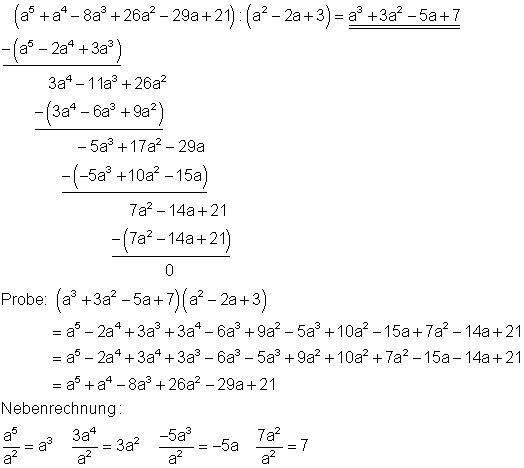
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
3. g) Ausführliche Lösung
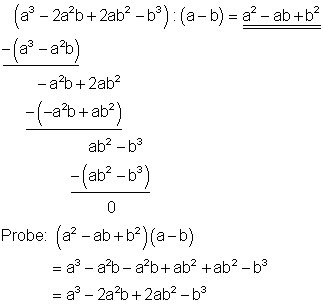
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
3. h) Ausführliche Lösung
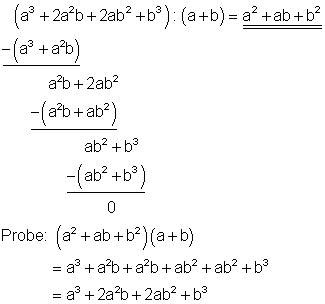
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
4. Führe die Polynomdivision durch!
a) Ausführliche Lösung
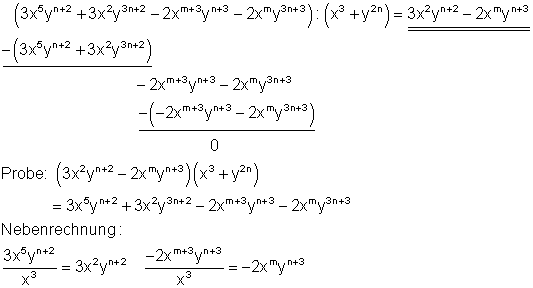
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
4. b) Ausführliche Lösung
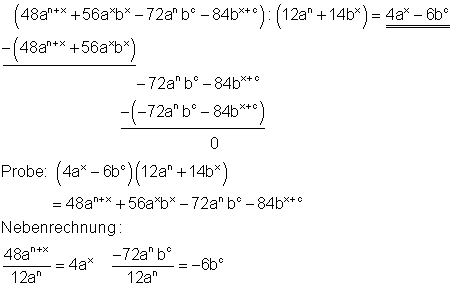
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
4. c) Ausführliche Lösung
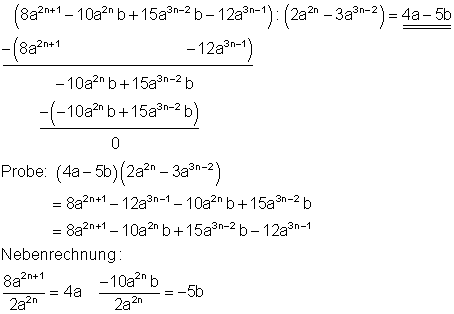
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
4. d) Ausführliche Lösung
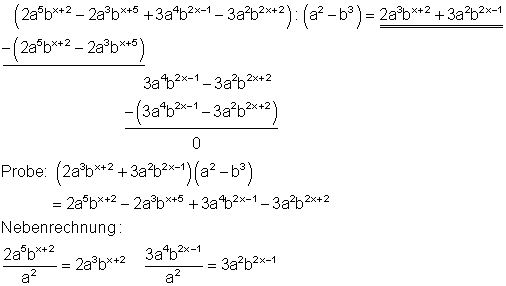
Starthilfe: Man verfährt hier ebenso wie unter 1a und 1c erklärt.
Hier findest du die Aufgaben.
Und hier die dazugehörige Theorie: Polynomdivision.
Hier eine Übersicht über weitere ganzrationale Funktionen, darin Links zu weiteren Aufgaben.


