Um den Graphen einer ganzrationalen Funktion zeichnen zu können, benötigt man eine Wertetabelle und die Achsenschnittpunkte. Deshalb zeige ich, wie man Wertetabelle mithilfe des HORNER-Schemas berechnet. Anschließend erkläre ich, wie man die Nullstelle mithilfe des Koeffizienten a0 finden kann. Zuletzt stelle ich Trainingsaufgaben zum zeichnen des Graphen zur Verfügung.
Wertetabelle mithilfe des HORNER-Schemas berechnen:
Dazu kannst du dir das 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
Wir können die Wertetabelle für eine ganzrationale Funktion berechnen, indem wir alle benötigten Funktionswerte mit dem Taschenrechner ausrechnen. Einfach ist es oft jedoch, wenn wir sie mithilfe des HORNER-Schemas ausrechnen.
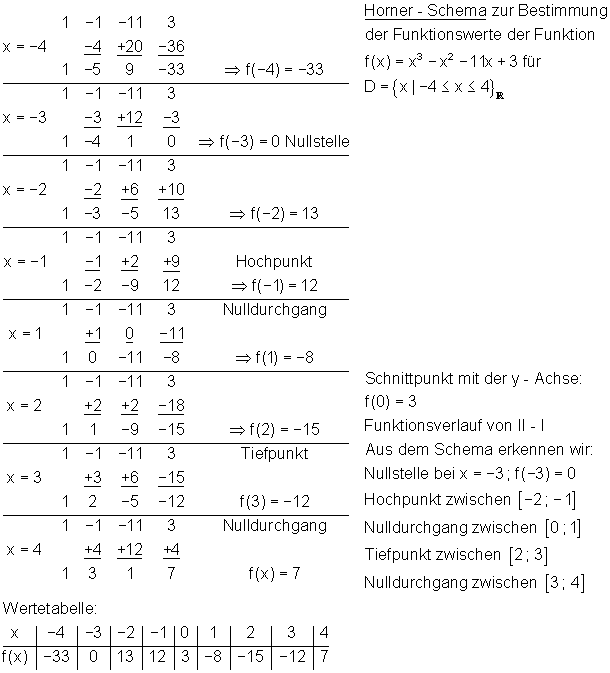
Nachfolgend stelle ich das Prinzip des Horner-Schemas grafisch dar.
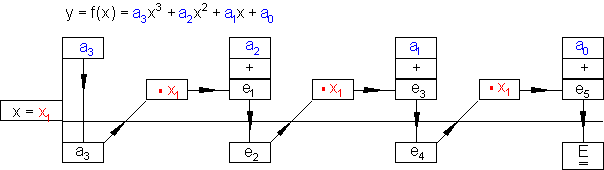
Berechnung der Nullstellen:
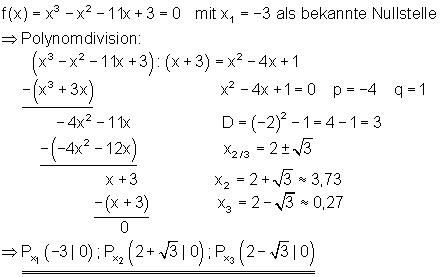
Danach kann man den Funktionsgraph zeichnen.
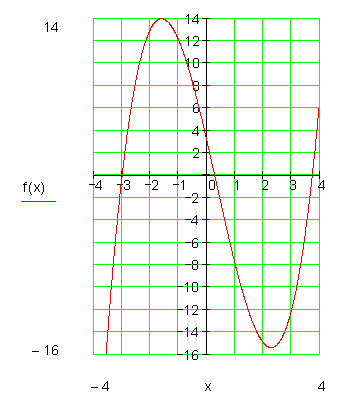
Allerdings können wir noch nicht den Hoch- und Tiefpunkt des Graphen bestimmen. Dazu benötigen wir die Differentialrechnung in einem späteren Kapitel.
Das Problem bei einer ganzrationalen Funktion höheren Grades eine oder mehrere Nullstellen zu finden, lässt sich manchmal durch zielstrebiges Raten lösen. Hierbei kann der Koeffizient a0 hilfreich sein. Teiler von a0 können dabei eventuell weiterhelfen.
Nullstelle mithilfe des Koeffizienten a0 finden:
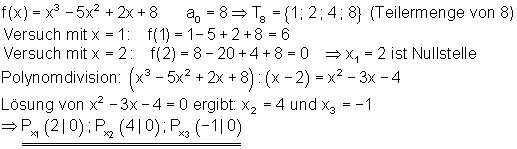
Hierzu nun einige Aufgaben:
Aufgaben I HORNER-Schema, Achsenschnittpunkte, Wertetabelle, Graphen:
Mache eine Aussage über das Symmetrieverhalten. Berechne danach mit dem Horner-Schema die Funktionswerte im angegebenen Intervall, (Schrittweite 0,5). Bestimme anschließend die Achsenschnittpunkte. Stelle außerdem eine Wertetabelle auf und zeichne den Graphen in ein Koordinatensystem. (Maßstab:1 EH/cm)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Aufgaben II Achsenschnittpunkte, Wertetabelle, Graphen:
Mache eine Aussage über das Symmetrieverhalten. Berechne die Funktionswerte im angegebenen Intervall, (Schrittweite 0,5) bestimmen Sie die Achsenschnittpunkte, stelle eine Wertetabelle auf und zeichne den Graphen in ein Koordinatensystem. (Maßstab:1 EH/cm)
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Dazu findest du hier die Lösungen
Interaktiv: Graphen zeichnen: Gob Koeffizienten und die Potenz für x ein, dann zeichnet das Javascript den Graphen.
Und hier eine Übersicht über weitere ganzrationale Funktionen, darin auch Links zu weiteren Aufgaben.
