In diesem Beitrag findet ihr zuerst eine Aufgabe zur Integralrechnung mit einem Werbebanner. Danach gibt es zwei weitere Aufgaben. Die Anforderungen sind dabei: Ableitung, Extremwerte, Fläche zwischen Graphen, e-Funktion, Produktregel, Kettenregel, Nullprodukt, Tangente.
1. Aufgaben Integralrechnung Werbebanner
Eine Werbefläche soll so gestaltet werden, dass das einbeschriebene Rechteck den größtmöglichen Flächeninhalt hat. Dabei wird der Mund mit einem einbeschriebenen Rechteck für Werbesprüche dargestellt. Die Randkurven des Mundes werden dabei durch nebenstehende Funktionsgleichungen dargestellt:
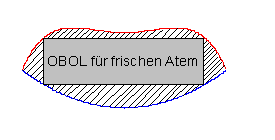
![]()
a) Welche Funktion beschreibt den oberen Teil des Mundes und welche den unteren Teil? Begründe deine Antwort.
b) Der Hersteller des Moduls für die Laufschrift benötigt die genauen Maße des Rechtecks. Bestimme die Seiten a und b des Rechtecks so, dass der Flächeninhalt maximal wird. Wie groß ist die Fläche? Die Längeneinheit ist Meter.
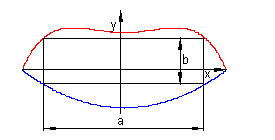
c) Der gesamte Mund soll in eine Hauswand integriert werden, dazu benötigt der Bauingenieur die benötigte Fläche.
d) Die schraffierte Fläche soll mit einer hochwertigen Leuchtfarbe versehen werden. Die Beschichtung von einem Quadratmeter kostet 120 €. Wie teuer wird die gesamte Beschichtung?
Anforderungen: Ableitung, Extremwerte, Fläche zwischen Graphen.
2. Bestimme die Fläche
Bestimme die Fläche zwischen den Graphen von f(x) und t(x), wenn t(x) die Tangente an f(x) im Punkt P( 2 | f(2) ) darstellt.
![]()
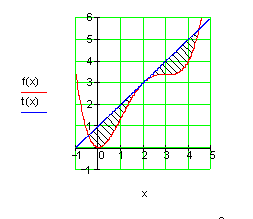
Anforderungen: Tangente, Nullstellen, Horner-Schema, bestimmtes Integral.
3. Nullstellen, Tangente
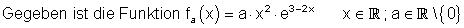
a) Bestimme die Nullstellen von f(x) und kommentiere dein Ergebnis.
b) Finde die Punkte mit waagerechten Tangenten und mach eine Aussage über die Lage dieser Punkte.
Anforderungen: Ableitung, e-Funktion, Produktregel, Kettenregel, Nullprodukt, Tangente.
Dazu findest du hier die Lösungen.
Und hier die Theorie: Differentations- und Integrationsregeln.
Hier eine Übersicht über alle Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

