Ich erkläre was Exponentialfunktionen, die Zahl e und e-Funktionen sind. Dazu erkläre ich wie man e-Funktionen spiegeln, verschieben, strecken und stauchen kann. Außerdem ihre Eigenschaften und die graphische Darstellung.
- Definition Exponentialfunktion
- Beispiele
- Graphen von Exponentialfunktionen mit unterschiedlichen Basen
- Die Zahl e mit Hilfe der Zinseszinsrechnung entwickeln
- Der Wert von e
- Spiegelung, Verschiebung und Streckung der e-Funktion
- Links zu Trainingsaufgaben
Es gibt Funktionen, in denen der Exponenten eine Zahlen ist. z. B. f(x) = 2x3.
Definition Exponentialfunktionen:
Es gibt jedoch auch Funktionen mit positiver Basis, bei denen die unabhängige Variable x als Exponent auftritt. Deshalb nennt man sie Exponentialfunktionen. Z. B. f(x) = 1,5x.
Hierbei bildet die Zahlen 1,5 die Basis und x den Exponenten.
Die Basis e nennt man auch Eulersche Zahl. Sie hat ungefähr den Wert 2,71828.
Im Folgenden wird sie noch eine wichtige Rolle spielen.
Graphen von Exponentialfunktionen mit unterschiedlichen Basen:
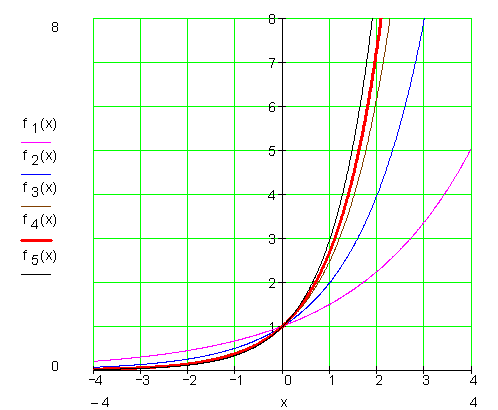
Der rot stark hervorgehobene Graph gehört zu der Exponentialfunktion mit der Basis e. Deshalb wir sie e-Funktion genannt.
Auffälligkeiten der e-Funktion
-
- Alle im Koordinatensystem dargestellten Graphen schneiden die y-Achse im Punkt Py ( 0 | 1 ).
-
- Für große negative x-Werte nähern sich alle Graphen beliebig der x-Achse. Jedoch schneidet sie die x-Achse nicht. In einem solchen Fall wird die negative x-Achse Asymptote genannt. Mit anderen Worten, die Graphen nähern sich für große negative x-Werte asymptotisch der x-Achse.
In mathematischer Schreibweise sieht das folgendermaßen aus:
\lim \limits_{x\to - \infty} a^x =0
Für große positive x-Werte wachsen die Funktionswerte über alle Grenzen. Mit anderen Worten gegen unendlich.
In mathematischer Schreibweise sieht das folgendermaßen aus:
\lim \limits_{x\to\infty} a^x = \infty
- Für große negative x-Werte nähern sich alle Graphen beliebig der x-Achse. Jedoch schneidet sie die x-Achse nicht. In einem solchen Fall wird die negative x-Achse Asymptote genannt. Mit anderen Worten, die Graphen nähern sich für große negative x-Werte asymptotisch der x-Achse.
- Dabei sind alle Funktionswerte der im Koordinatensystem dargestellten Graphen positiv. Denn für Exponentialfunktionen sind nur positive Basen zugelassen. Folglich gibt es in diesem Fall keine Nullstellen.
![]()
Zahl e mit Hilfe der Zinseszinsrechnung entwickeln:
Dabei verwenden wir die in jeder Formelsammlung enthaltene Zinseszinsformel.

Z. B. soll sich das Kapital bei jährlicher Verzinsung verdoppeln. Also müssen wir einen Zinsfuß von p = 100% wählen, so dass p/100 = 1 ist.
Wenn wir mehrere Zinsabschnitten pro Jahr haben, wird das Kapital mit Zinseszins mehrfach verzinst. Dabei muss der Zinsfuß durch die Anzahl der Zinsabschnitte geteilt werden.
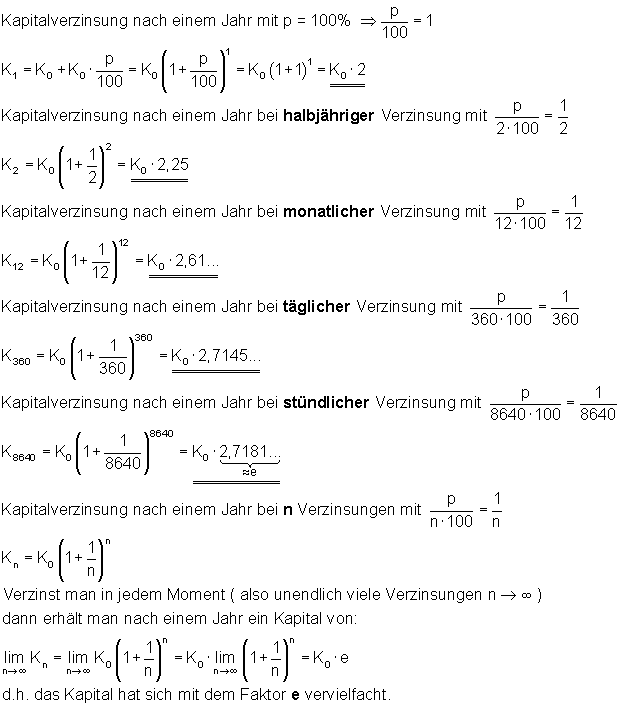
Der Wert von e
Die meisten Taschenrechner haben eine e-Funktionstaste, ähnlich wie die pi-Taste. Damit kann man sich den Wert von e anschauen. Der Zahlenwert der Eulerschen Zahl ist ein unendlich nicht periodischer Dezimalbruch. Dabei bildet die Zahl e die Basis der e-Funktion.
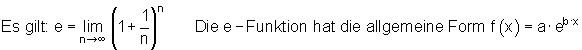
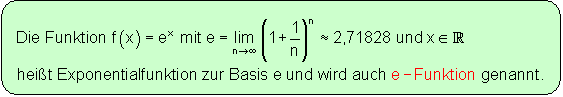
Im Folgenden stelle ich Grundeigenschaften der e-Funktion f(x) = ex vor.
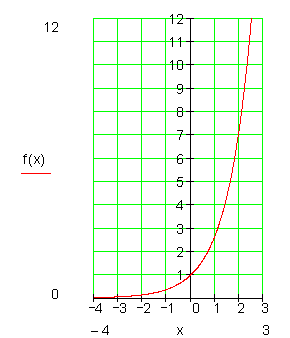
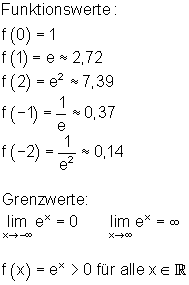
Die e-Funktion besitzt keine Nullstellen, keine Extremwerte und auch keine Wendepunkte.
Spiegelung, Verschiebung und Streckung der e-Funktion
Wenn man Normalparabeln verschiebt, entstehen andere Parabeln. Genauso kann man auch e-Funktion verschieben, strecken oder spiegeln. Daraus entstehen andere Exponentialfunktionen.
Im folgenden zeige ich das an Beispielen:
e-Funktion spiegeln:
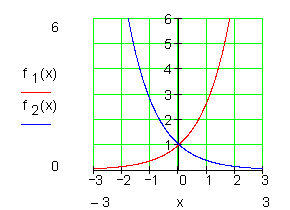

Hierbei entstehen keine Nullstellen, Extremwerte und Wendepunkte.
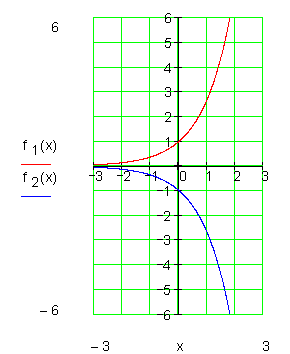

Ebenso keine Nullstellen, Extremwerte und Wendepunkte.
e-Funktion in y-Richtung verschieben


Weiterhin keine Nullstellen, Extremwerte und Wendepunkte.
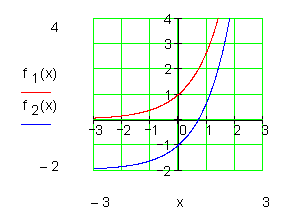

Ebenfalls keine Extremwerte und Wendepunkte.
Aber es gibt eine Nullstelle im Intervall [ 0 ; 1 ]
e-Funktion in x-Richtung verschieben
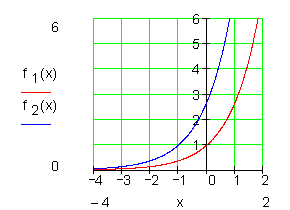

Ebenso keine Nullstellen, Extremwerte und Wendepunkte.
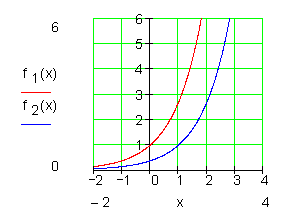

Weiterhin keine Nullstellen, Extremwerte und Wendepunkte.
e-Funktion in y-Richtung strecken und stauchen
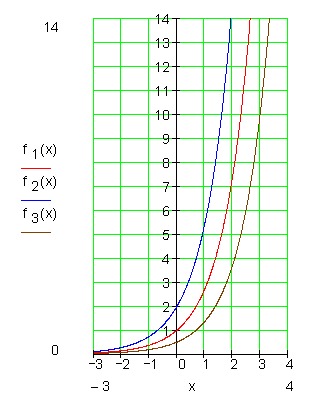

Ebenfalls keine Nullstellen, Extremwerte und Wendepunkte.
e-Funktion in x-Richtung strecken und stauchen
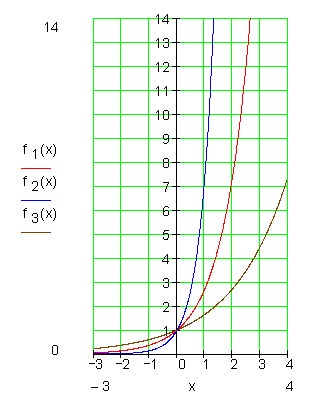
Wenn wir mit mit dem Faktor \color{blue}{k = 2} stauchen:
\color{blue}{f_2(x) = e^{2 \cdot x}} .
Dann ist der Schnittpunkt mit der y-Achse
f_2(0) = e^0 = 1 \Rightarrow P_y(0 | 1) .
Randgrenzwerte
\lim\limits_{x \to - \infty}(e^{2 \cdot x}) = 0 \, \, \, \lim\limits_{x \to \infty}(e^{2 \cdot x}) = \infty .
Wenn wir mit dem Faktor \color{red}{k = \frac{1}{2}} strecken:
\color{red}{f_3 = e^{\frac{1}{2}x}} .
Dann ist der Schnittpunkt mit der y-Achse
f_3(0) = e^0 = 1 \Rightarrow P_y(0 | 1) .
Randgrenzwerte
\lim\limits_{x \to - \infty}(e^{\frac{1}{2}x}) = 0 \, \, \, \lim\limits_{x \to \infty}(e^{\frac{1}{2}x}) = \infty .
Ebenfalls keine Nullstellen, Extremwerte und Wendepunkte.
Spiegelungen, Verschiebungen und Streckungen der e-Funktion lassen sich genauso miteinander kombinieren.
e-Funktion auf der x- und y-Achse verschieben
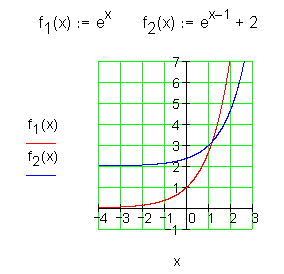
Wenn wir f1 (x) auf der x-Achse um eine Einheit nach rechts und auf der y-Achse um zwei Einheiten nach oben verschieben, entsteht f2 (x).
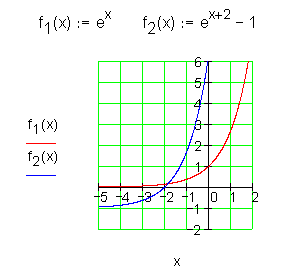
f2 (x) entstanden aus f1 (x) durch:
Verschiebung auf der x-Achse um zwei Einheit nach links.
Verschiebung auf der y-Achse um eine Einheiten nach unten.
Weitere Aufgaben: Potenzen VIII Potenzen mit e-Funktionen
Hier findest du eine Übersicht über alle Beiträge zum Thema Fortgeschrittene Differential- und Integralrechnung, dort auch Links zu weiteren Aufgaben.


