In diesem Beitrag zeige ich anhand vieler Beispiele, wie man Wurzelgleichungen und Exponentialgleichungen löst. Außerdem gehe ich auf die Lösungsmenge ein und zeige Problemlösungen.
- Wurzelgleichungen: Defintion und Lösungsverfahren
- Problem: zu viele Lösungen
- Exponentialgleichungen lösen
- Wann eine Lösung mittels Exponentenvergleich möglich ist
- Was man nicht logarithmieren kann
Wurzelgleichungen lösen Beispiel 1
Gleichungen, in denen Wurzelterme vorkommen, nennt man Wurzelgleichungen. Im folgenden Beispiel erkläre ich das Lösungsverfahren.
Wie bei allen Gleichungen gehören dabei zur Lösungsmenge von Wurzelgleichungen nur Elemente aus der Definitionsmenge D, für die man jede Gleichung bestimmen muss.
Rechnung:
Wenn man den linken Wurzelterm mit T1 und den rechten mit T2 bezeichnet, dann gilt:
Weil die Definitionsmenge von Quadratwurzeln keine negativen Radikanden in IR zulässt, gilt:
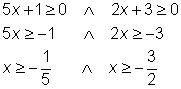
Definitionsmenge von T1:
Definitionsmenge von T2:
Die Definitionsmenge D ist dabei die Schnittmenge der Definitionsmengen, von T1 und T2.
Es gehören also nur solche Elemente zur Definitionsmenge, die größer oder gleich -1/5 sind.
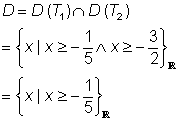
Zur Bestimmung der Lösungsmenge muss man die in der Gleichung vorkommenden Quadratwurzeln beseitigen. Das macht man, indem man beide Seiten der Gleichung quadriert. ausmultipliziert und nach x umformt.
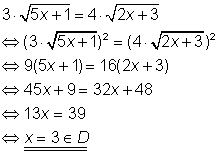
Zur Probe setzt man das Lösungselement in die Wurzelgleichung ein:
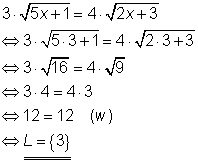
Wenn man x = 3 in die Wurzelgleichung eingibt, dann ergibt sich eine wahre Aussage. Dadurch bestätigt sich die die Richtigkeit der Lösung.
Problem: zu viele Lösungen
Ist das Potenzieren der Quadratwurzeln eine Äquivalenzumformung oder kann durch das Quadrieren noch ein weiteres Element hinzukommen, das gar nicht zu der ursprünglichen Gleichung gehört?
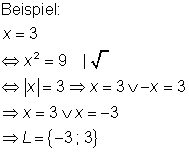
Durch das Quadrieren ist also das Element -3 zusätzlich hinzugekommen. Es ist daher nicht nur wichtig, sondern unbedingt erforderlich, nach einer Umformung durch Potenzieren auf beiden Seiten der Gleichung die Probe zu machen.
Wurzelgleichungen lösen Beispiel 2
Hier ein weiteres Beispiel zum Lösen von Wurzelgleichungen:
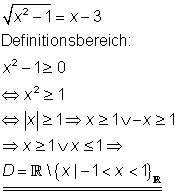
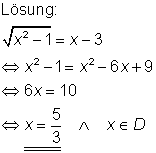
Mit anderen Worten: es gibt keinen Wert für x der obige Gleichung erfüllt.
Wurzelgleichungen lösen Beispiel 3
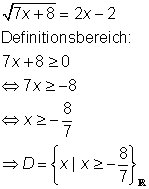
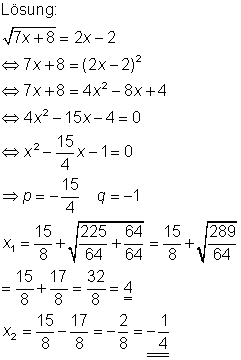
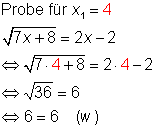
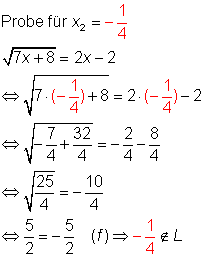
Wurzelgleichungen lösen Beispiel 4
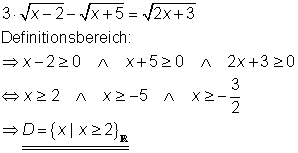
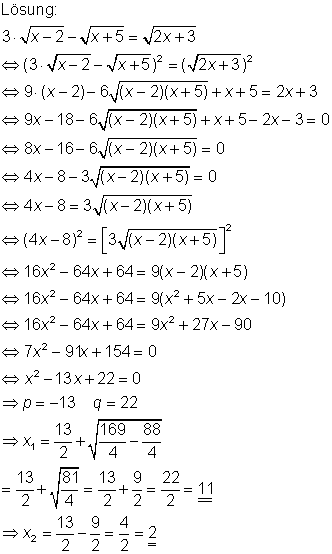
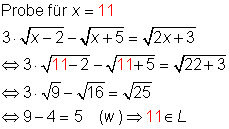
Exponentialgleichungen lösen Beispiel 1:
Aussageformen, bei denen die Lösungsvariable in Exponenten von Wurzeln oder Potenzen vorkommen, heißen Exponentialgleichungen oder – ungleichungen.
Die Lösungsmengen solcher Aussageformen kann man meistens durch Anwendung der Logarithmengesetze ermitteln.
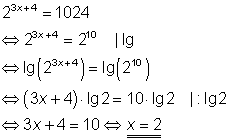
Wann eine Lösung mittels Exponentenvergleich möglich ist
Eine Lösung mittels Exponentenvergleich ist nur dann möglich, wenn es gelingt, die Terme auf beiden Seiten der Aussageform so umzuformen, dass sich Potenzen mit gleichen Basen ergeben.
Exponentialgleichungen lösen Beispiel 2
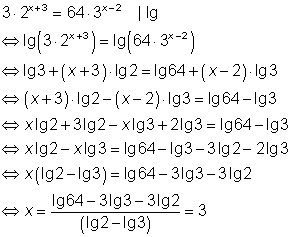
Welche Exponentialgleichungen man nicht logarithmieren kann
Exponentialgleichungen, in denen Summen oder Differenzen vorkommen, kann man nicht logarithmieren. Man kann jedoch versuchen, sie mittels Substitution (Einsetzung einer Ersatzvariablen) zu lösen.
Exponentialgleichungen lösen Beispiel 3
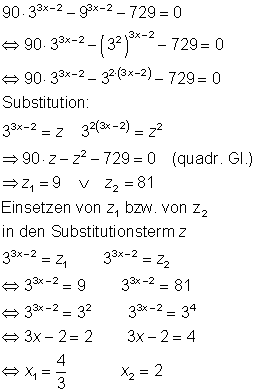
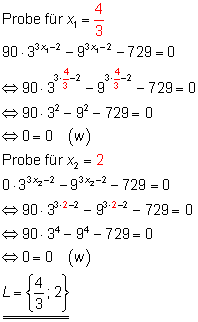
Hilfreich sind ebenfalls die Regeln zum Lösen von Exponentialgleichungen.
Dazu findest du hier Aufgaben Exponentialgleichungen I.
Außerdem Aufgaben Exponentialgleichungen II mit e-hoch-x.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.
