In diesem Beitrag gebe ich eine Zusammenfassung der Regeln zum Lösen von Exponentialgleichungen. Zuerst stelle ich ein Beispiel vor. Danach zeige ich nacheinander den Logarithmus eines Produktes, eines Quotienten, einer Potenz, Logarithmus von der Basis, Logarithmus von der Zahl 1, Die wichtigsten Potenzgesetze, Logarithmus im Exponenten. Zuletzt eine Tabelle zur Umrechnung von einem Logarithmensystem in ein anderes.
Am Anfang fragt man sich oft: Wie gehe ich vor? Deshalb gebe ich hier ein paar praktische Tipps:
Wenn es gelingt, die Terme auf beiden Seiten der Exponentialgleichung so umzuformen, dass sich Potenzen mit gleichen Basen ergeben, dann ist eine Lösung mittels Exponentialvergleich möglich.
In vielen Fällen führt der Ansatz über das Logarithmieren zum Erfolg.
Exponentialgleichungen, in denen Summen oder Differenzen vorkommen, können nicht logarithmiert werden. Dann kann man versuchen, sie mittels Substitution (Einsetzung einer Ersatzvariablen) zu lösen.
Hier ein
Beispiel für die Lösung einer Exponentialgleichung durch Logarithmieren
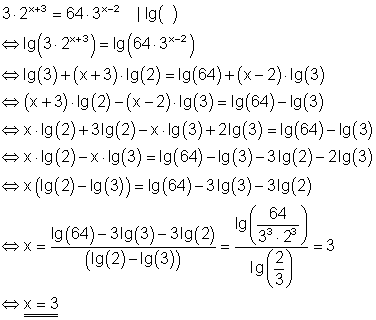
Logarithmus eines Produktes
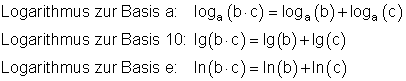 .
.
Merke: Der Logarithmus eines Produktes ist gleich der Summe der Logarithmen der einzelnen Faktoren.
Dazu kannst du dir dieses 📽️ shorts Logarithmen multiplizieren ansehen.
Beispiel zum Logarithmus zur Basis e:
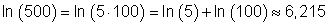
Logarithmus eines Quotienten
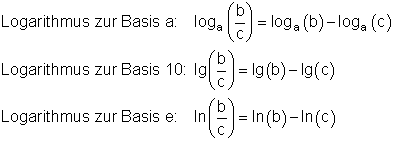
Merke: Der Logarithmus eines Quotienten ist gleich der Differenz der Logarithmen von Dividend (Zähler) und Divisor (Nenner).
Dazu kannst du dir dieses 📽️ shorts Logarithmen dividieren ansehen.
Beispiel zum Logarithmus zur Basis e:
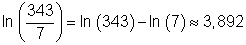
Logarithmus einer Potenz
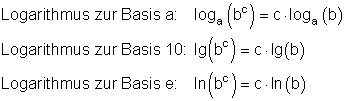
Merke: Der Logarithmus einer Potenz ist gleich dem Logarithmus der Basis multipliziert mit dem Exponenten.
Dazu kannst du dir dieses 📽️ shorts Logarithmus einer Potenz berechnen ansehen.
Beispiel zum Logarithmus zur Basis e:
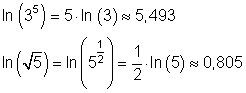
Logarithmus von der Basis
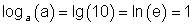
Merke: Der Logarithmus zur Basis a von der Basis a ist 1.
Beispiel zum Logarithmus zur Basis e:
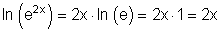
Logarithmus von der Zahl 1
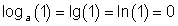
Merke: Der Logarithmus der Zahl 1 ist in jedem Logarithmensystem gleich Null.
Die wichtigsten Potenzgesetze
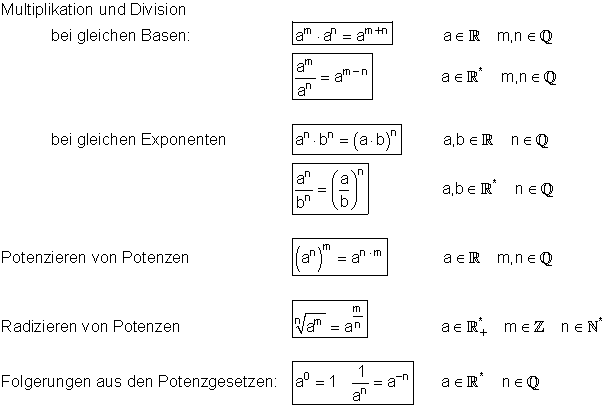
Logarithmus im Exponenten
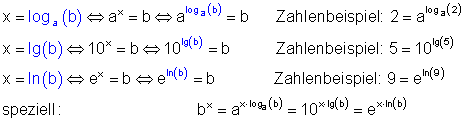
Die obigen Beziehungen sind für die Umformung von Termen oft nützlich.
Umrechnung von einem Logarithmensystem in ein anderes
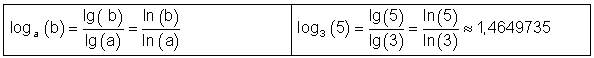
Hier findest du die Theorie: Exponentialgleichungen.
Hier kannst du nochmal alles zu Logarithmen nachlesen.
Und hier die Playlist aller Videos dazu: 📽️ Videos zu Logarithmen.
Und hier die Aufgaben hierzu Exponentialgleichungen I.
Hier eine Übersicht über weitere Beiträge zu Gleichungen, darin auch Links zu weiteren Aufgaben.


