Hier findest du die Lösungen Exponentialgleichungen Brüche.
1. Löse die Gleichungen!
Ausführliche Lösungen:
a)
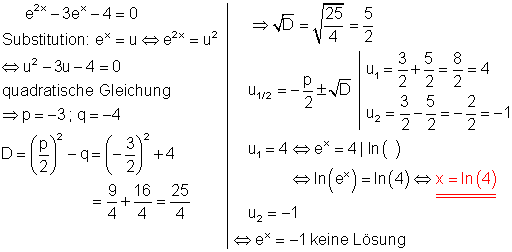
b)
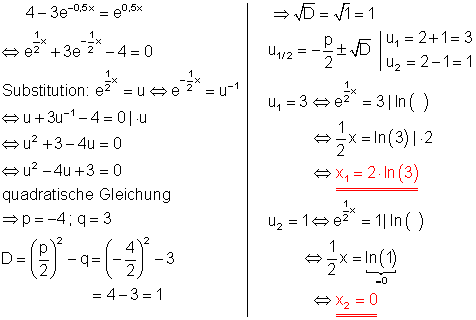
2. Löse die Gleichungen!
Ausführliche Lösungen:
a)
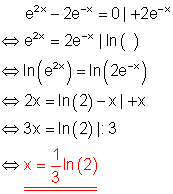
b)
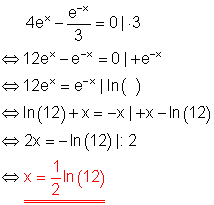
c)
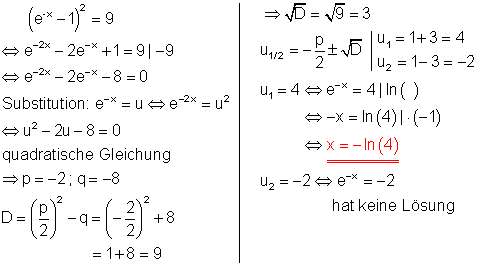
d)
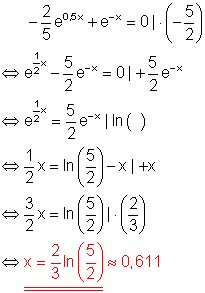
Lösungsweg:
Nach einfacher algebraischen Umformung (Multiplikation mit -5/2) werden die beiden Summanden getrennt, so dass auf jeder Seite der Gleichung logarithmiert werden kann. Durch Logarithmieren mit dem Logarithmus zur Basis e (auch Logarithmus naturalis genannt), entsteht eine Gleichung mit der Variablen x, bei der x nicht mehr im Exponenten vorhanden ist. Die Lösung erhält man, indem die Gleichung nach der Variablen x umgeformt wird.
3. Löse die Gleichungen!
Ausführliche Lösungen:
a)
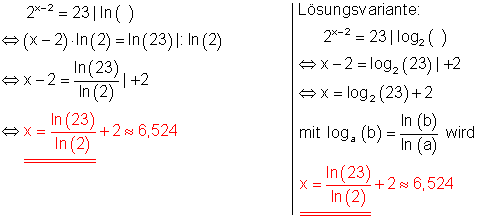
b)
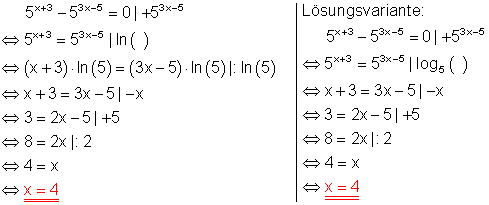
c)
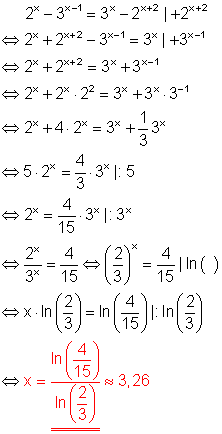
Lösungsweg:
Die Gleichung wird so umgeformt, dass auf jeder Seite nur Potenzen mit gleichen Basen stehen.
Potenzgesetz:
Potenzen mit gleichen Basen werden multipliziert, indem man die Exponenten addiert. Anwendung des Gesetzes führt dazu, dass es nur noch die Basen 2 und 3 mit dem Exponenten x gibt.
Potenzgesetz:
Potenzen mit ungleichen Basen aber gleichen Exponenten werden dividiert, indem man die Basen dividiert und den Exponenten beibehält.
Logarithmieren beider Seiten führt zum Ergebnis.
d)
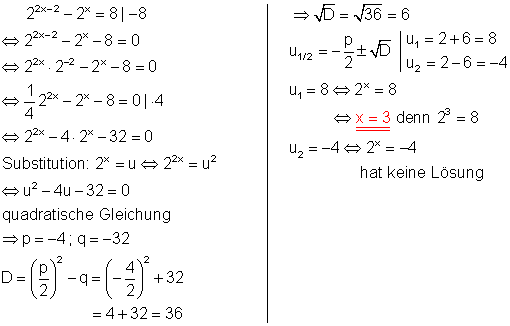
e)
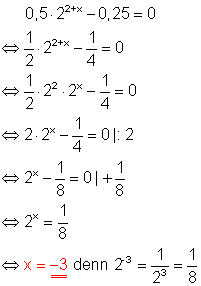
Lösungsweg:
Dezimalzahlen werden in Brüche verwandelt.
Potenzgesetz:
Potenzen mit gleichen Basen werden multipliziert, indem man die Exponenten addiert. Anwendung des Gesetzes führt dazu, dass die Potenz zur Basis 2 nur noch die Variable x im Exponenten hat.
Anwendung der Regel für negative Exponenten.
f)

4. Für welche Werte von k hat die Gleichung eine Lösung?
Ausführliche Lösungen:
a)
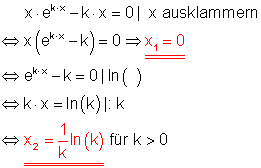
b)
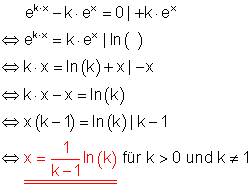
c)
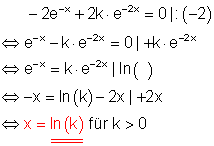
Lösungsweg:
Die Potenzen zur Basis e werden auf unterschiedliche Seiten der Gleichung gebracht, damit die Gleichung logarithmierbar wird. Anwendung der Logarithmengesetze führt zu einer Gleichung in x.
5. Löse die Gleichungen!
Ausführliche Lösungen:
a)
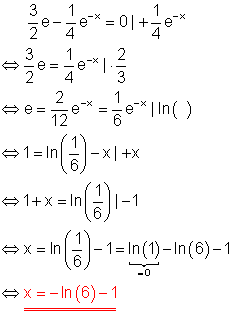
b)
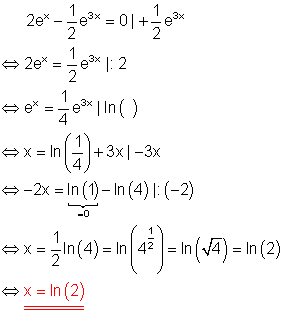
c)
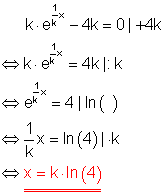
d)
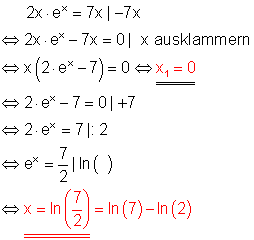
e)
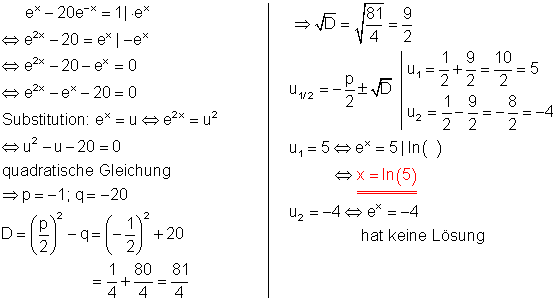
f)
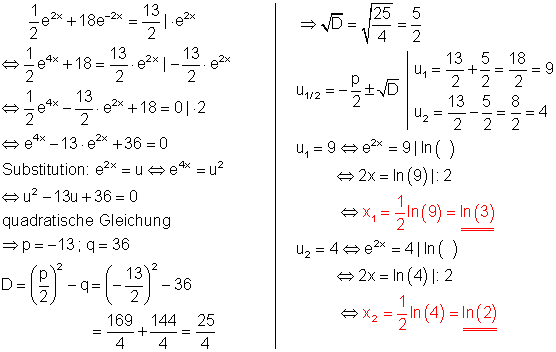
6. Löse die Gleichungen!
Ausführliche Lösungen:
a)
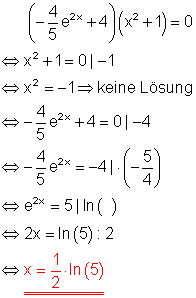
b)
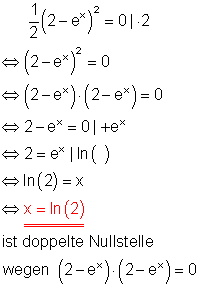
c)
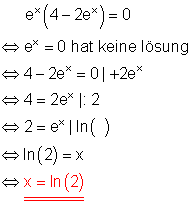
d)
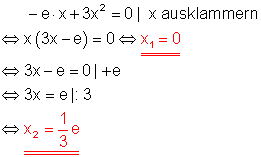
e)
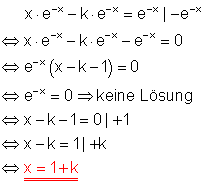
f)
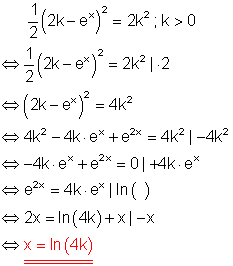
7. Löse die Gleichungen!
Ausführliche Lösungen:
a)
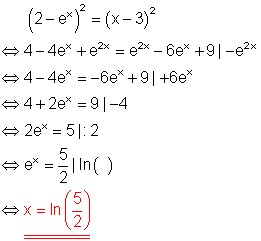
b)
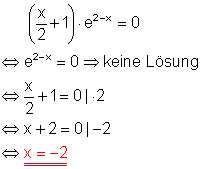
c)
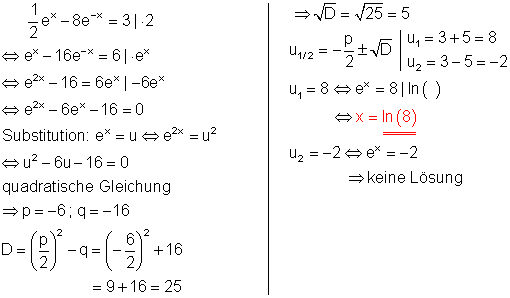
d)
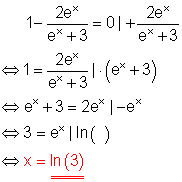
Lösungsweg:
Die Summanden werden getrennt. Die Bruchgleichung wird mit dem Nenner der rechten Seite multipliziert. So entsteht eine Gleichung ohne Brüche. Umformen und Logarithmieren führt zum Ergebnis.
e)
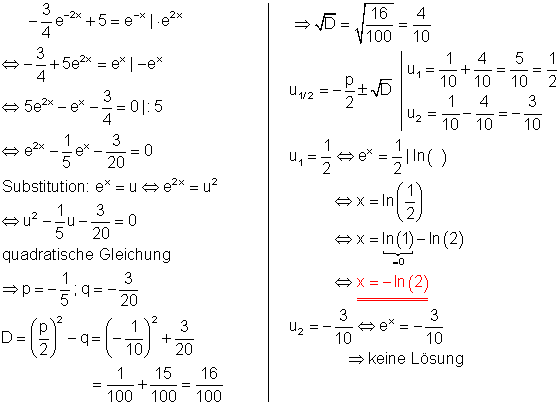
f)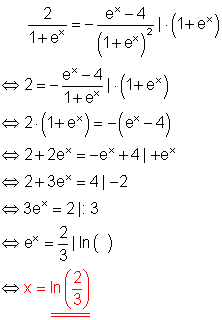
Lösungsweg:
Zweifache Multiplikation mit dem Nenner der linken Seite lässt den Bruchterm verschwinden. Bei der algebraischen Umformung ist darauf zu achten, dass der Bruchstrich die Klammer ersetzt.
Ausmultiplizieren und weitere algebraische Umformungen führen zu einer Gleichung, die sich leicht logarithmieren lässt.
8. Löse die Gleichungen!
Ausführliche Lösungen:
a)
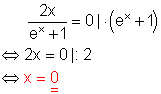
Lösungsweg:
Multiplikation mit dem Nenner der linken Seite lässt den Bruchterm verschwinden.
b)
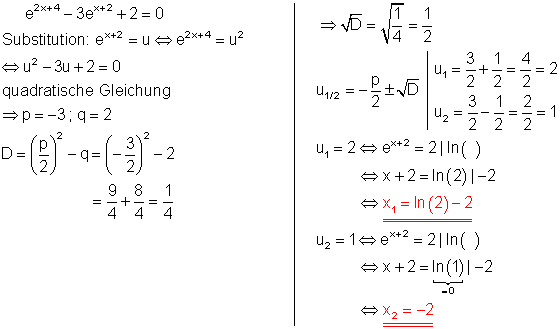
c)
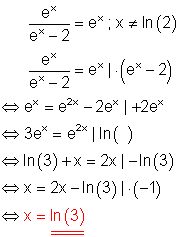
Lösungsweg:
Die Definitionsmenge ist eingeschränkt, da der Nenner der linken Seite nicht Null werden darf.
Multiplikation mit dem Nenner der linken Seite lässt den Bruchterm verschwinden.
Algebraische Umformungen ermöglichen das Logarithmieren.
d)
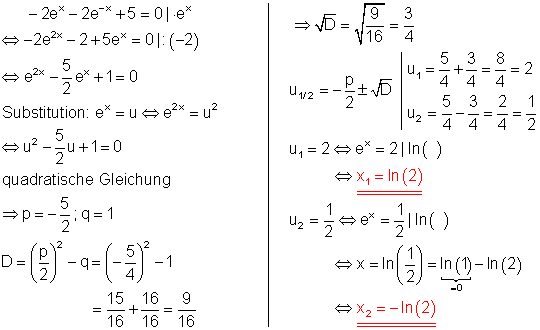
e)
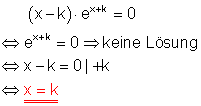
f)
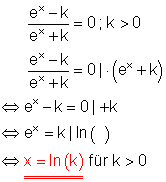
Hier finden Sie die Aufgaben hierzu.
Und hier die Theorie: Exponentialgleichungen
und Exponentialfunktionen und die e-Funktion.
Hier eine Übersicht über weitere Beiträge zu Gleichungen, darin auch Links zu weiteren Aufgaben.

