Wie wir bereits in dem Beitrag Steigung und Tangente gesehen haben, ist die Steigung eines Funktionsgraphen in einem Punkt P ( x0 | f (x0) ) gleichbedeutend mit der Tangentensteigung in diesem Punkt. Deshalb werde ich in diesem Beitrag zeigen, wie wir Tangente und Normale berechnen, mit anderen Worten: Wie man eine Tangentengleichung bestimmt. Als erstes werde ich anschauliche Beispiele vorstellen, danach die allgemeine Herleitung der Tangenten- und Normalengleichung.
- Tangentensteigerung berechnen
- Die Graphen
- Zusammenhang von Steigung, Ableitung, Tangente
- Normalengleichung berechnen
- Tangente durch Einsetzen des Punktes berechnen
- Tangente durch die Ableitung berechnen
- Anwendungsbeispiel Tangentengleichung
- Zusammenfassung der Vorgehensweise
- Links zu Trainingsaufgaben und weiteren Beiträgen
Tangentensteigung berechnen
Dazu betrachten wir die Funktion f(x) und deren Ableitungsfunktion etwas genauer.

Hierzu stellen wir sowohl für die Funktion, wie auch für deren Ableitungsfunktion eine Wertetabelle auf:

Aus der Wertetabelle können wir dann den Scheitelpunkt der quadratischen Funktion f(x) ablesen:

Mit anderen Worten: im Scheitelpunkt S ist die Steigung von f(x) Null.
Die Tangente in S hat ebenfalls die Steigung Null, sie verläuft dort waagerecht.
Hier die Graphen:
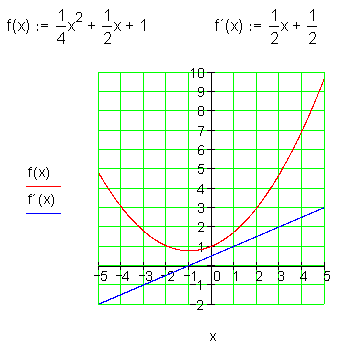

Zusammenhang von Steigung, Ableitung, Tangente:
Einsetzen eines x-Wertes in f(x) ergibt die y-Koordinate von P ( x | y ).
Einsetzen eines x-Wertes in f'(x) ergibt die Steigung des Graphen oder die Steigung der Tangente von f(x) im Punkt P ( x | y ).
Die Steigung des Graphen einer Funktion f(x) in einem Punkt P(x0|y0), ist gleich der Steigung mt der Tangente t(x) in diesem Punkt. Außerdem ist diese Steigung gleich der ersten Ableitung in diesem Punkt f'(x0).
Also: Steigung von f(x) in P(x0|y0)
= Steigung mt der Tangente t(x) in P(x0|y0)
= f'(x0) also Ableitung im Punkt P(x0|y0).
Tangentengleichung und Normalengleichung berechnen
Die Normale ist eine Gerade, die senkrecht zur Tangente an einen Graphen durch deren Berührungspunkt verläuft.
Gegeben ist die Funktion
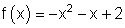
Als nächstes bestimmen wir die Gleichung für Tangente und Normale an der Stelle x0 = 2, anders ausgedrückt für den Punkt P ( 2 | f(2) ).
Vorüberlegung zum Tangente, Normale berechnen:
Die Tangente ist eine Gerade mit der Gleichung:![]()
Die Normale ist eine dazu senkrechte Gerade:![]() . Das nennt man auch den negativ reziproken Wert, also negativ und umgedrehter Bruch.
. Das nennt man auch den negativ reziproken Wert, also negativ und umgedrehter Bruch.
Die Steigung der Tangente entspricht der Steigung des Graphen von f(x) im Punkt P.
Vorgehensweise beim Tangente, Normale berechnen:
Wir setzen den Wert für x0 in den Funktionsterm von f(x) ein. Damit erhalten wir die fehlende Koordinate von P.
Dann leiten wir die Funktion f(x) ab.
Danach setzen wir den Wert für x0 in den Ableitungsterm f'(x) ein. Da f'(x) die Steigungsfunktion von f(x) ist, erhalten wir somit die Steigung mt der Tangente in P.
Für die Tangentengleichung t(x) = mtx + bt brauchen wir noch bt. Dazu gibt es zwei Möglichkeiten:
Tangente durch Einsetzen des Punktes berechnen
Die Steigung mt und die Koordinaten des Punktes P setzen wir als nächstes in die Tangentengleichung ein. Damit erhalten wir den Ordinatenabschnitt bt der Tangente und die Tangentengleichung ist fertig.
Um die Gleichung der Normalen zu erhalten, verfahren wir analog, verwenden für deren Steigung jedoch den negativ reziproken Tangentensteigungswert.
Nachfolgende Rechnung das verdeutlicht dies:
Rechnung Tangente, Normale berechnen:

Die Methode zur Berechnung der Tangente ist vergleichbar mit der, eine Geradengleichung aufzustellen, von der man die Steigung und den Punkt P kennt, durch den sie verläuft.
Siehe auch Berechnung der Funktionsgleichung einer Geraden Fall I.
Hier die Graphen:
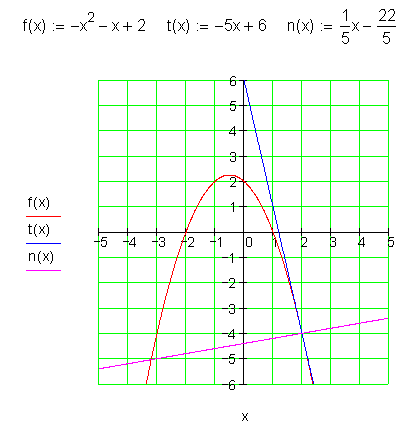
Dazu kannst du dir das 📽️ Video Tangente im Punkt P berechnen ansehen.
Allgemeine Herleitung der Tangenten- und Normalengleichung
Hier die zweite Möglichkeit, um die Tangentengleichung zu bestimmen:
Damit man nicht in jedem einzelnen Fall obige Rechnung erneut durchführen muss, leiten wir nun eine allgemeine Formel her.
Die Tangente soll den Graphen von f(x) im Punkt P (x0 | f(x0) ) berühren.
Die Normale soll den Graphen von f(x) im Punkt P (x0 | f(x0) ) senkrecht schneiden.
Herleitung:

Auch das kannst du dir in dem 📽️ Video Tangente im Punkt P berechnen ansehen.
Anwendungsbeispiel Tangentengleichung:
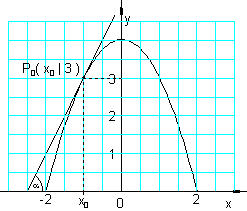
Eine Leiter soll so an einen Heuhaufen gelehnt werden, dass sie den Haufen in einer Höhe von 3 m vom Boden aus berührt.
Der Heuhaufen hat die Form einer umgestülpten Parabel, ist 4 m hoch und hat an der Basis einen Durchmesser von ebenfalls 4 m.
Unter welchem Winkel muss die Leiter angelegt werden?
Wie weit vom Fuß des Heuhaufens muss die Leiter auf dem Boden aufgesetzt werden?
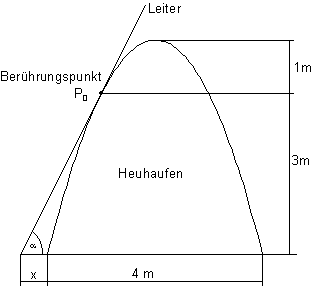
Wir legen die y – Achse durch den Scheitelpunkt des Graphen.
Die Parabel hat die Funktionsgleichung:

Tangente berechnen:

Der Abstand vom Heuhaufen, wo die Leiter aufgesetzt werden muss, ist der Abstand zwischen der Nullstelle von f(x) und der Nullstelle von t(x).
Nullstellen:
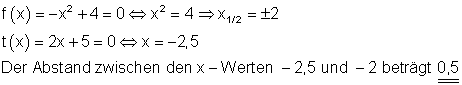
Die Leiter muss also 0,5 m vom Fuß des Heuhaufens entfernt auf den Boden aufgesetzt werden.
Aus dieser Aufgabenstellung haben wir gelernt, wie man die Gleichung einer Tangente bestimmt, die den Graphen in einem definierten Punkt berührt.
Beispiel:
Wir ermitteln die Gleichung der Tangente, die den Graphen von f(x) im Punkt P berührt.
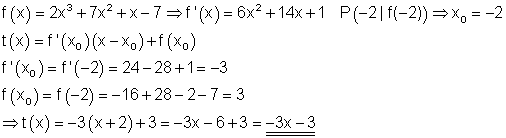
ZusammenfassungTangente, Normale berechnen:
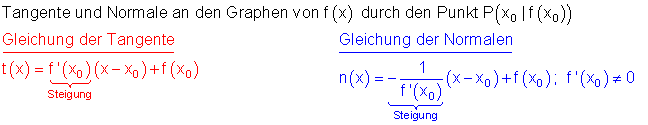
Wie geht man vor, wenn wir die Formel anwenden?
Wenn die Koordinate x0 bekannt ist.
Die 2. Koordinate von P erhält man durch Einsetzen von x0 in den Term von f(x).
Dann bilden wir die Ableitung von f(x), also f'(x).
Die Steigung der Tangente erhält man durch Einsetzen von x0 in den Term von f'(x).
Danach setzt man die berechneten Werte in die Gleichung für Tangente bzw. Normale ein und vereinfacht diese durch Umformen.


