Hier findet ihr eine Übersicht über Differentationsregeln und Integrationsregeln.
- Ableitung und Aufleitung elementarer Funktionen
- Gegenüberstellung von Differentationsregeln und Integrationsregeln
- Weitere Regeln für die Differentialrechnung
- Aufgaben zu Integrationsregeln
- Weitere Regeln für die Integralrechnung
- Aufgaben: Ableiten und integrieren mit e-Funktionen
- Links zu weiteren Aufgaben
Ableitung und Aufleitung elementarer Funktionen
Funktion |
Ableitung |
Stammfunktion |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Gegenüberstellung von Differentationsregeln und Integrationsregeln
Konstantenregel
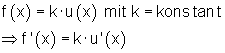
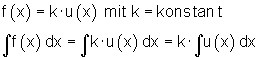
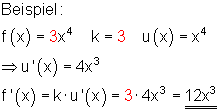
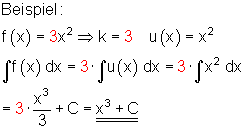
Summenregel
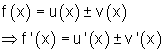
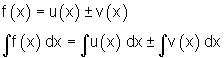
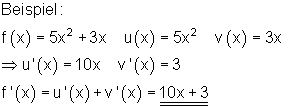
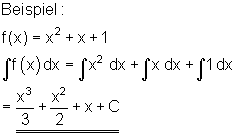
Weitere Regeln für die Differentialrechnung
| Produktregel: |  |
| Beispiel: |  |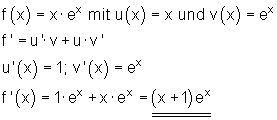
| Quotientenregel: |  |
| Beispiel: |  |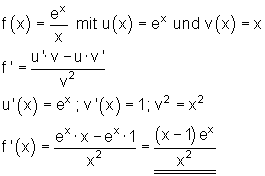
| Kettenregel: |  |
| Beispiel: |  |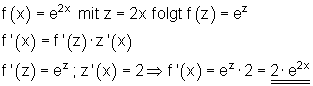
Aufgaben zu Integrationsregeln:
Produktregel, Quotientenregel, Kettenregel
Differenziere folgende Funktionen mit den bekannten Regeln.
- f(x) = (x + a)^2 - e^{2x-3}
2. f(x) = (1 - e^{ax})^2
3. f(x) = (e^{2x} + e^{-x})^2
4. f(x) = (x + 1) e^x
5. f(x) = (3 - 2x) e^{-\frac{1}{2}x}
6. f(x) = a(x - 3)e^{4x-3}
7. f(x) = \dfrac{x^2 + 1}{e^x}
8. f(x) = \dfrac{e^x - 1}{e^x + 1}
9. f(x) = \frac{x}{x - 1}
10. f(x) = \frac{1}{x} (x^2 -4)
Hier findest du die Lösungen dazu.
Weitere Regeln für die Integralrechnung
Vertauschen der Integrationsgrenzen
Durch Vertauschen der Integrationsgrenzen ändert sich das Vorzeichen des Integrals.
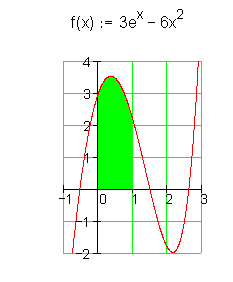
Die gekennzeichnete Fläche soll berechnet werden.
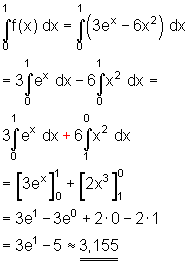
Das Nullintegral:
Sind obere und untere Grenze beim bestimmten Integral gleich, so ist der Wert des bestimmten Integrals Null.
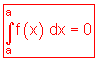
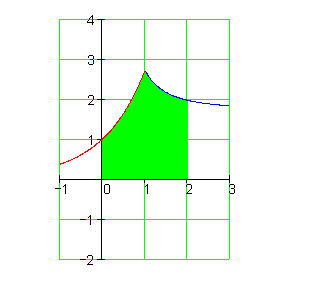
Intervalladdition
Der Wert des gesamten Integrals ergibt sich durch Summierung der Integrale über alle Teilbereiche.
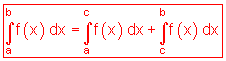
Aufgaben: Ableiten und integrieren mit e-Funktionen:
Differenziere folgende Funktionen:
1. f(x) = e^{-4x} - e^{4x}
2. f(x) = \frac{3}{2} e^{-5x^2-3x}
3. f(x) = -4e^x (e^{-x} + 3)
4. f(x) = -e^{t-x} - 2t \cdot e^{-tx}
5. f(x) = t \cdot e^{2-3x} - 6e^{x^2+3}
6. f(x) = t (e^{-x} - 3x^2)
Integriere folgende Funktionen und kontrolliere die Ergebnisse durch Ableiten!
7. f(x) = \frac{1}{16} (x^2 - 3e^x)
8. f(x) = x^3 - 2x^2 + 4x + \frac{3}{x}
9. f(x) = t \cdot x - \frac{3}{2} e^x + t^2 + 2e
10. f(x) = t^2x (x^2 - 8x)
Integration der e-Funktion, Flächenberechnungen.
Und hier eine Übersicht über alle Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.
