Hier findet ihr Aufgaben zur Differential- und Integralrechnung, die Anforderungen an die Aufgaben sind: Ableitung, Tangente, Normale, Nullstellen, Dreiecksfläche, Achsenschnittpunkte, Wendepunkt, Wendetangente, Geradenschnittpunkt, e-Funktionen, Ableitung, Extremwerte, Fläche, Integration, uneigentliche Integrale.
1. Berechne die Fläche des Dreiecks,
welches durch die Tangente t(x) und der Normalen n(x) mit der x-Achse gebildet wird.
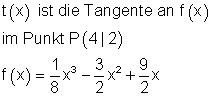
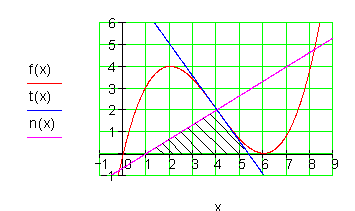
Anforderungen: Ableitung, Tangente, Normale, Nullstellen, Dreiecksfläche
2. Berechne die Fläche des gekennzeichneten Dreiecks, wenn
![]()
g(x) ist die Gerade durch die Achsenschnittpunkte von f(x).
t(x) ist die Wendetangente von f(x).
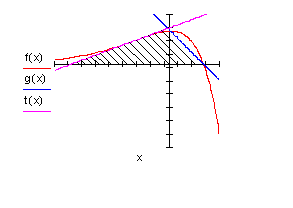
Anforderungen: Achsenschnittpunkte, Wendepunkt, Wendetangente, Geradenschnittpunkt.
3. Schnittpunkt
![]()
a) Berechne den Schnittpunkt von f(x) mit der y-Achse.
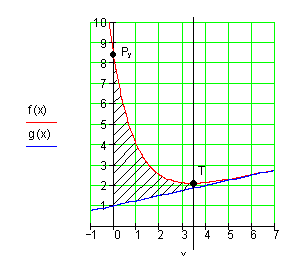
b) Bestimme die Gleichung der Geraden g(x). Welche Bedeutung hat diese Gerade?
c) Berechne den Tiefpunkt T ( xe | f(xe) )
d) Berechne die gekennzeichnete Fläche.
e) Auf welchen Wert ändert sich die Fläche, wenn die rechte Grenze gegen unendlich geht?
Anforderungen: e-Funktionen, Achsenschnittpunkte, Ableitung, Extrempunkte, Fläche, Integration, uneigentliches Integral.
Dazu findest du hier die Lösungen.
Und hier die Theorie: Differentations- und Integrationsregeln.
Hier eine Übersicht über alle Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.
