Im letzten Beitrag hatten wir uns mit Extrempunkten in der Differentialrechnung beschäftigt. Diese brauchen wir um Wendepunkt, Sattelpunkt und Wendetangente zu berechnen. Zuerst erkläre ich anhand von Beispielen aus der Praxis diese Begriffe. Damit es leicht verständlich ist, stelle ich zuerst Wendepunkte beim Radfahren vor, danach Wendepunkte in der Mathematik. Danach zeige ich die Berechnung eines Wendepunkts anhand eines Beispiels mit Kommentar. Dann zeige ich die Berechnung des Sattelpunkts und die Ermittlung der Wendetangente. Schließlich stelle ich ein Beispiel aus der Kostenrechnung vor.
- Beispiele für Wendepunkte beim Radfahren.
- Wendepunkte in der Mathematik
- Berechnung der Wendepunkte, Beispiel mit Kommentar, Links zu Aufgaben und Video
- Berechnung des Sattelpunktes mit Video
- Berechnung der Wendetangente
- Beispiel aus der Kostenrechnung
- Links zu Aufgaben
Beispiele 1 Wendepunkt beim Radfahren:
Du startest mit dem Fahrrad bei A, durchfährst eine S-Kurve und fährst dann weiter bis B.
Betrachte dazu bitte mal die jeweilige Lenkerstellung auf der Fahrstrecke.
Nachdem du durch die Linkskurve (Lenkerstellung nach links) fährst, fährst du durch die Rechtskurve (Lenkerstellung nach rechts).

Irgendwo zwischen der Linkskurve und der Rechtskurve muss der Lenker einmal gerade gestanden haben.
Mit anderen Worten: Wir hatten einen Wendepunkt.
Beispiel 2 beim Radfahren auf einem Berg:
Du fährst mit dem Fahrrad durch hügeliges Gelände.
Nachdem du die Talsohle durchfahren hast, beginnt die Straße anzusteigen.
Zuerst sanft, dann immer stärker.
Dann nimmt die Steigung wieder ab, um oben auf dem Berg den Wert Null zu erreichen.
Irgendwo auf der Strecke war der Anstieg am größten.
Mit anderen Worten: Dort befindet sich der Wendepunkt.

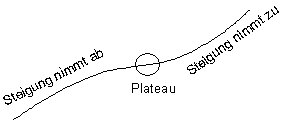
Beispiel 3 Radfahren, Steigung nimmt zu:
Eine andere Situation des Radfahrers ist Grafik unten zu entnehmen:
Bei einer Bergfahrt nimmt die Steigung zunächst ab, um dann erneut wieder anzusteigen.
Dazwischen befindet sich ein Gebiet mit geringer Steigung (Plateau).
Im Bereich des Plateaus ist der Anstieg der Strecke am geringsten.
Dort befindet sich der Wendepunkt.
Wendepunkte in der Mathematik
Wir wissen, das die erste Ableitung einer Funktion die Steigungsfunktion ist, aus deren Graphen man die Steigung ablesen kann.
Da der Wendepunkt der Punkt mit der größten oder auch kleinsten Steigung sein soll, findet man ihn, indem man die Extremwerte der Ableitungsfunktion bestimmt. Dieses Verfahren ist das gleiche, wie bei der Bestimmung der Ursprungsfunktion f(x), bezieht sich aber jetzt auf die Ableitungsfunktion f'(x).
Fassen wir die Bedingungen für Wendepunkte zusammen:

Berechnung der Wendepunkte Beispiel mit Kommentar:

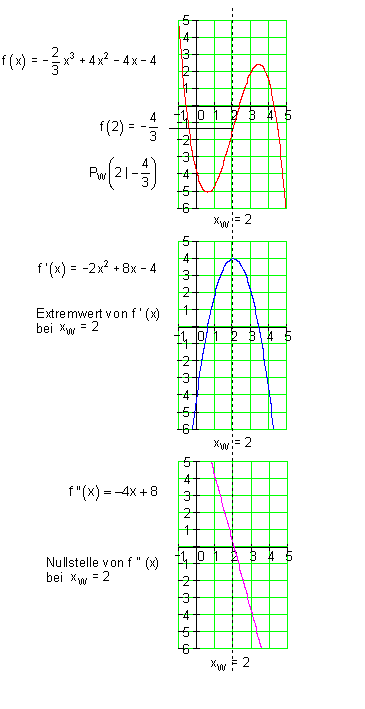
Merke:

Dazu kannst du dir das 📽️Video Wendepunkte ansehen.
Hier findest du Aufgaben hierzu.
Berechnung des Sattelpunkts
Eine besondere Form des Wendepunktes ist der Sattelpunkt.
Das ist ein Wendepunkt mit der Steigung Null.
Nähert man sich von links, so glaubt man es käme ein relatives Maximum.
Nähert man sich von rechts, so glaubt man es käme ein relatives Minimum.
Es gibt jedoch keine Extremwerte. Wir untersuchen diesen Fall nun mathematisch:
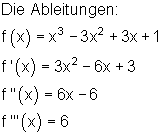
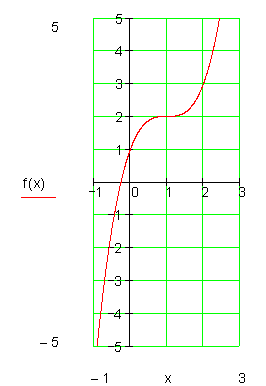

Ermittlung der Wendetangente
Die Tangente an den Funktionsgraphen im Wendepunkt heißt Wendetangente.
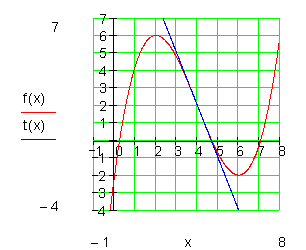
Die Gleichung der Wendetangente wird ebenso bestimmt wie die Tangentengleichung in einem beliebigen Punkt des Graphen. Wir berechnen also f“(x) =0 für den Wendepunkt. f“'(x) muss außerdem ungleich Null sein. Wir den gefundenen x-Wert in f(x) ein und haben dadurch die Koordinaten des Wendepunktes. Die Steigung der Wendetangente berechnen wir schließlich genauso mithilfe der bekannten Gleichung.
Beispiel:
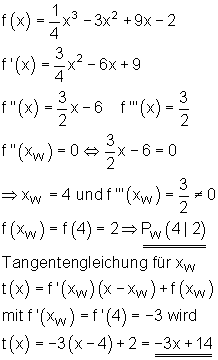

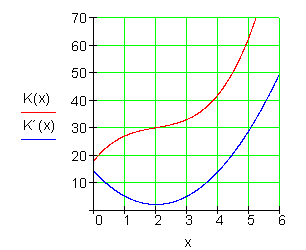
Beispiel aus der Kostenrechnung
Für welche Ausbringungsmenge x wird bei gegebener Kostenfunktion der Kostenzuwachs am geringsten?
Dazu gibt es unter Kostenrechnung als Anwendung der Differentialrechnung ein ausführliches Beispiel.
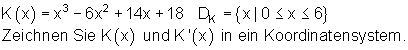

Dazu findest du hier Aufgaben zur Differentialrechnung IX.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.


