Bei diesen Aufgaben geht es darum, ganzrationale Funktionen auf Wendestellen zu untersuchen und gegebenenfalls die Wendepunkte zu bestimmen.
Die Lösungen findest du weiter unten.
Aufgaben: Untersuche auf Wendestellen und bestimme gegebenenfalls die Wendepunkte
Dazu kannst du dir das 📽️Video Wendepunkte ansehen.
1.
f(x) = \dfrac{1}{4}x^3 - \dfrac{3}{2}x^2 + 5 Lösung
2.
f(x) = \dfrac{1}{2}x^3 - 4x^2 + 8x Lösung
3.
f(x) = \dfrac{1}{4}x^3 - \dfrac{3}{2}x^2 + 3x - 1 Lösung
4.
f(x) = -\dfrac{1}{4}x^3 + \dfrac{3}{2}x^2 + 1 Lösung
5.
f(x) = \dfrac{1}{3}x^3 + x^2 - 2x - 1 Lösung
6.
f(x) = \dfrac{1}{2}x^4 - 3x^2 +\dfrac{3}{2} Lösung
7.
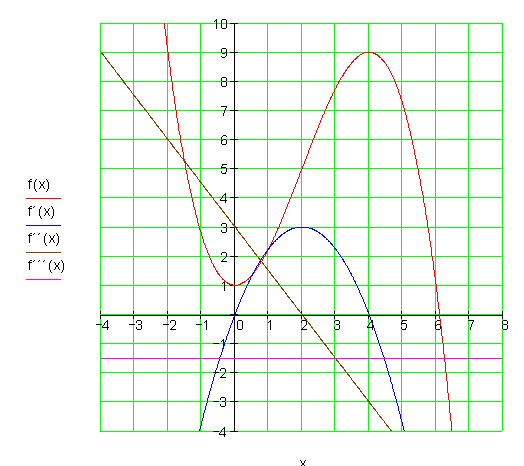
f(x) = -\dfrac{1}{2}x^4 + 3x^2 - 1 Lösung
8.
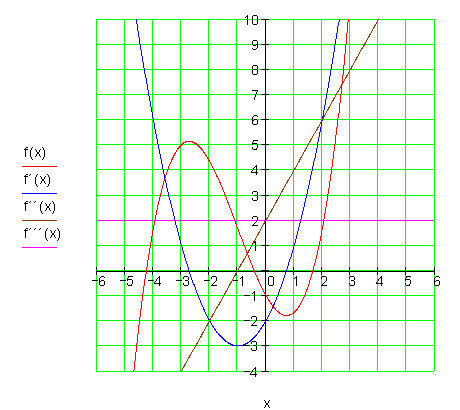
f(x) = \dfrac{1}{4}x^4 - x^3 + \dfrac{3}{2}x^2 - x + \dfrac{1}{2} Lösung
9.
f(x) = -\dfrac{1}{4}x^4 + x^3 + 1 Lösung
10.
f(x) = \dfrac{1}{12}x^4 - \dfrac{3}{2}x^2 - 1 Lösung
Lösungen
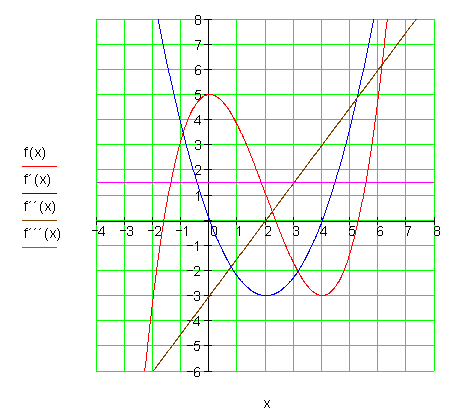
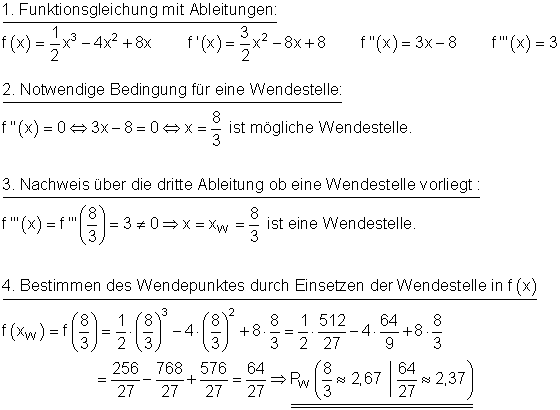
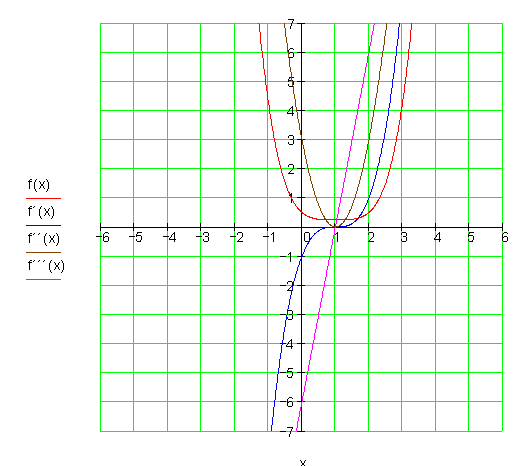
Die Graphen:![]()
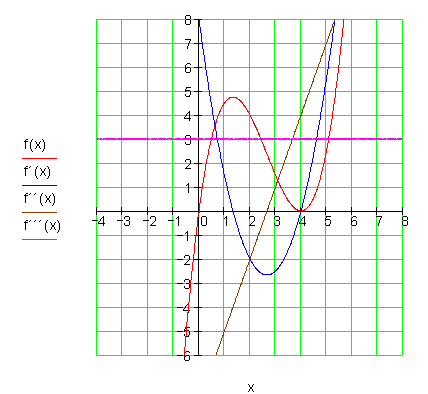

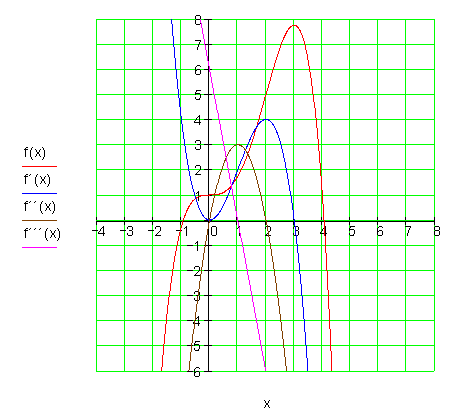
Die Graphen:![]()
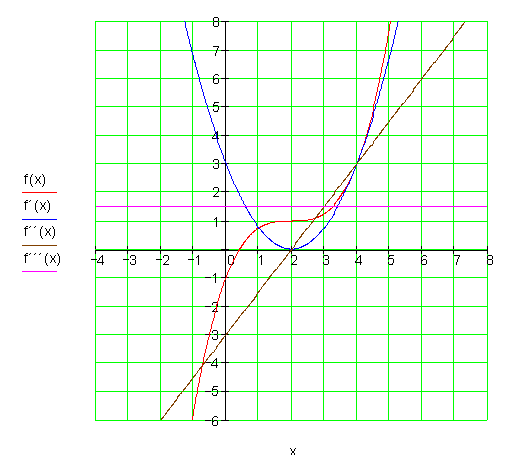

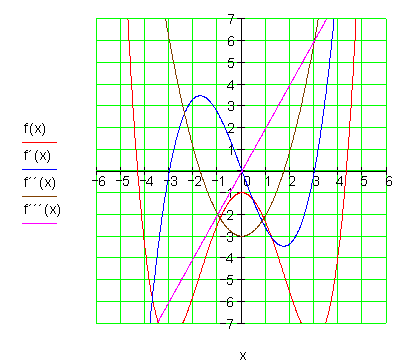
Die Graphen:![]()



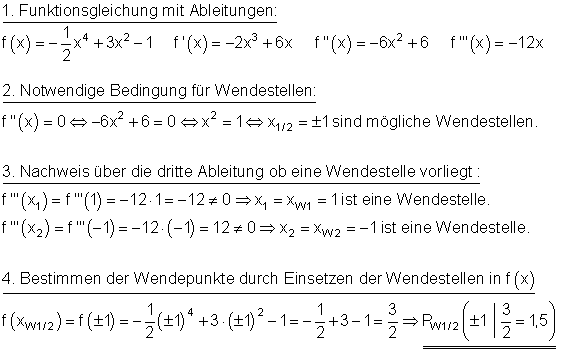


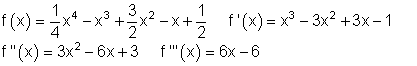

Die
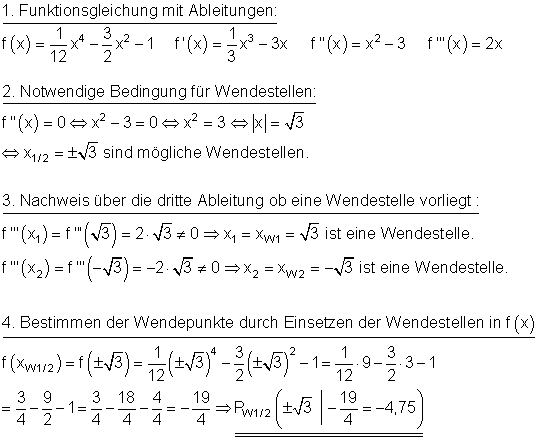
Dazu findest du hier die Theorie: Wendepunkt Sattelpunkt und Wendetangente.
Und hier eine Übersicht über alle Beiträge zum Thema Differentialrechnung.

