In diesem Beitrag werde ich zuerst erklären, was wir in der Differentialrechnung unter Monotonie verstehen. Danach stelle ich den Monotoniesatz vor und zeige anhand von anschaulichen Beispielen, wie man den Monotoniebereich bestimmt.
Monotonie, Monotoniesatz
Die lineare Funktion f(x) = a1x + a0 ist die einfachste Funktion, deren Graph keinerlei Krümmung aufweist. Verantwortlich dafür ist der konstante Anstieg a1 = tan(α). Wobei α der Winkel zwischen der Geraden und der positiv gerichteten x-Achse ist.

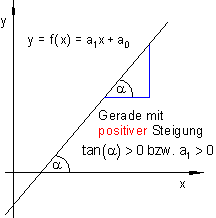

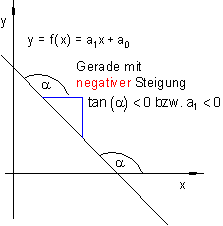

In beiden Fällen spricht man von einer monotonen Funktion, und zwar von einer monoton wachsenden Funktion, wenn a1 > 0 ist,
und von einer monoton fallenden Funktion, wenn a1 < 0 ist.
Der Begriff Monotonie lässt sich auch auf Funktionen übertragen, deren Kurvenverlauf gekrümmt ist, wenn man bedenkt, dass man im Allgemeinen in jedem Kurvenpunkt eine Tangente an den Graphen legen kann.
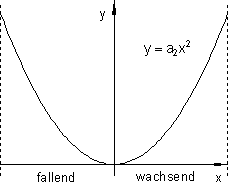

Der Anstieg des Graphen ist jetzt zwar nicht mehr konstant, wie dies bei der Geraden der Fall war, sondern er ändert sich von Kurvenpunkt zu Kurvenpunkt. Aber der Zusammenhang:
Wenn der Anstieg der Tangente > 0, dann ist die Kurve monoton wachsend.
Wenn der Anstieg der Tangente < 0, dann ist die Kurve monoton fallend.
Bekanntlich liefert die erste Ableitung der Funktion f(x) die Steigungsfunktion f'(x). Damit lässt sich der Monotoniesatz wie folgt formulieren:
Monotoniesatz:

Bestimmung der Monotoniebereiche
Beispiel:
Aus dem Funktionsgraphen lassen sich häufig die Monotoniebereiche mehr oder weniger genau ablesen.
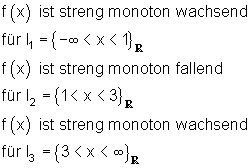
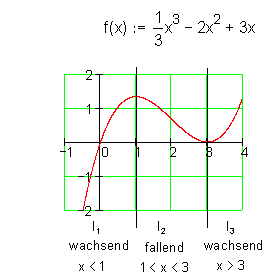
Beispiel:
Folgende Monotoniebereiche lassen sich aus dem Graphen ablesen:
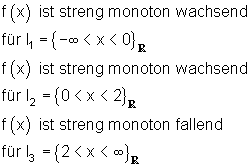

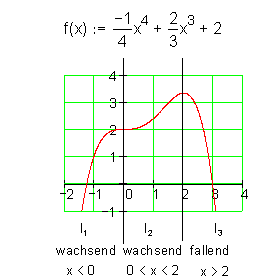

Mit der Monotonie werden wir uns bei der Kurvendiskussion befassen. Dort gibt es dann auch Aufgaben dazu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.


