Bevor ich erkläre, wie man Extrempunkte in der Differentialrechnung berechnen kann, muss ich einige Begriffe definieren: Hochpunkt, relatives (lokales) Maximum , Tiefpunkt und relatives (lokales) Minimum. Danach zeige ich, wie man die Extrempunkte des Graphen einer Funktion findet. Dann zeige ich den Nachweis für Extrempunkte über Vorzeichenwechsel von f'(x) und mit Hilfe der zweiten Ableitung von f(x). Danach erkläre ich anhand eines anschaulichen Beispiels, was notwendige und hinreichende Bedingungen sind. Schließlich zeige ich, was Relative und absolute Extrema sind.
- Wofür man Extrempunkte in der Differentialrechnung braucht
- Definitionen Hochpunkt, Maximum, Tiefpunkt
- Relatives Minimum und Maximum
- Nachweis für Extrempunkte über Vorzeichenwechsel von f'(x)
- Nachweis für Extrempunkte mit Hilfe der zweiten Ableitung von f(x)
- Zusammenfassung Extrempunkte
- kommentierte Beispiele
- notwendige und hinreichende Bedingungen
- Relative und absolute Extrema
- Links zu Aufgaben
Wofür man Extrempunkte in der Differentialrechnung braucht
Beim Zeichnen eines Funktionsgraphen war es bislang unbefriedigend, den Hochpunkt und den Tiefpunkt nicht zu kennen. Mit Hilfe der Differentialrechnung wollen wir nun versuchen, dieses Problem zu lösen.
Definitionen Hochpunkt, relatives (lokales) Maximum , Tiefpunkt und relatives (lokales) Minimum:
Ein Punkt H(x0 | f(x0) auf dem Graphen von f(x) heißt Hochpunkt, wenn f(x0) der größte Funktionswert für alle x aus der Umgebung von x0 ist.
Dieser grüßte Funktionswert f(x0) heißt relative (lokales) Maximum an der Stelle x0.
Ein Punkt T(x1 | f(x1)) auf dem Graphen von f(x) heißt Tiefpunkt, wenn f(x1) der kleinste Funktionswert für alle x aus einer Umgebung von x1 ist.
Dieser kleinste Funktionswert f(x1) heißt relatives (lokales) Minimum an der Stelle x1.
Hochpunkte bzw. Tiefpunkte nennt man also Extrempunkte des Graphen von f(x).
Der x-Wert eines Extrempunktes heißt folglich Extremstelle,
der Funktionswert einer Extremstelle heißt Extremwert.
Relatives Minimum und Maximum:
Statt relatives Maximum schreiben wir rel. Max.
Statt relatives Minimum schreiben wir rel. Min.
Statt H ( x0 | f(x0) ) schreiben wir PMax ( x0 | f(x0) ).
Statt T ( x0 | f(x0) ) schreiben wir PMin ( x0 | f(x0) ).
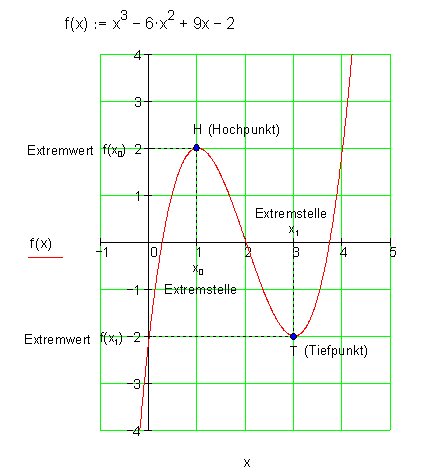
Wie findet man nun die Extrempunkte des Graphen einer Funktion f(x) ?
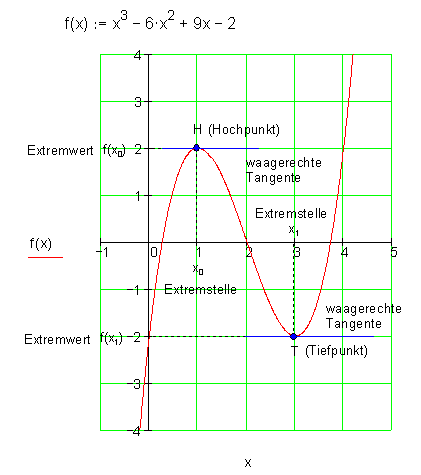
Eine Tangente, die an einem Extrempunkt einer dort differenzierbaren Funktion angelegt wird, ist immer waagerecht, sie hat die Steigung Null.
Da die Tangentensteigung in einem bestimmten Punkt auch immer die Steigung des Funktionsgraphen in diesem Punkt beschreibt, ist die Steigung des Funktionsgraphen in einem Extrempunkt auch immer gleich Null ist.
Die Ableitung einer Funktion erhält die Ableitungsfunktion. Diese beschreibt die Steigung der Funktion an jedem Punkt. Eine notwendige Bedingung für einen Extremwert ist also, dass die erste Ableitung an diesem Punkt Null ist.
Notwendige Bedingung für (lokale) Estremstellen: f'(x)=0.
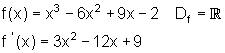
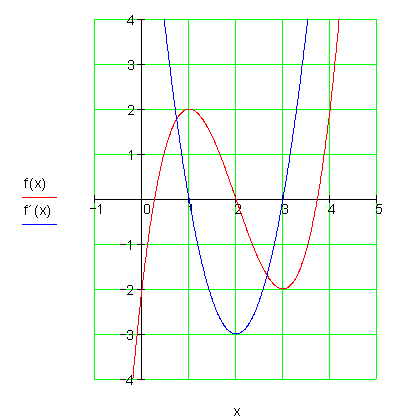
An der Grafik sehen wir, dass an den Extremstellen das Vorzeichen der Steigung wechselt.
Links vom Hochpunkt (relatives Maximum) ist die Steigung positiv und rechts vom relativen Maximum (rel. Max.) ist die Steigung negativ.
Links vom Tiefpunkt (rel. Min.) ist die Steigung negativ und rechts vom rel. Min ist die Steigung positiv.
In einer Umgebung vom rel. Max. bedeutet das also für die Ableitungsfunktion, dass deren Steigung negativ sein muss.
In einer Umgebung vom rel. Min. bedeutet das folglich für die Ableitungsfunktion, dass deren Steigung positiv sein muss.
Der Nachweis ob ein Extrempunkt Hochpunkt oder Tiefpunkt ist, lässt sich auf zwei Arten führen. Diese beiden werde ich im folgenden erklären.
1. Nachweis für Extrempunkte über Vorzeichenwechsel von f'(x)
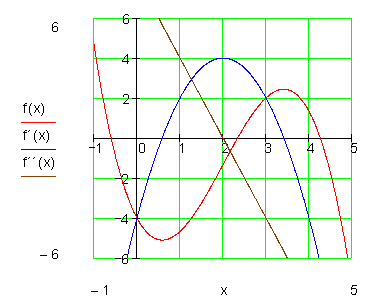
f(x) = x^3 - 6x^2 + 9x - 2
f'(x) = 3x^2 - 12x + 9
Notwendige Bedingung für Extrempunkte ist:
f'(x) = 0 \Leftrightarrow 3x^2 - 12x + 9 = 0
Denn dann ist die Tangente der ersten Ableitung waagerecht.
Um die Nullstellen zu finden, klammern wir die 3 aus:
3(x^2 - 4x + 3) = 0
Nullstellen sind oft Teiler des absoluten Gliedes, dadurch kommen wir auf:
f'(x) = 3(x-1)(x-3)
Die Extrempunkte sind also x1 = 1 und x2 = 3.
In dieser Tabelle können wir dann prüfen, ob an Extrempunkte ein Vorzeichenwechsel von f'(x) auftritt:

Wenn x < 1, dann ist (x-1) negativ und x-3 auch. Da beides multipliziert wird, ist f'(x) in dem Bereich positiv.
Bei x zwischen 1 und 3 ist, dann ist x-1 positiv, x-3 jedoch negativ. Die Multiplikation ist negativ, an der Stelle befindet sich also ein Vorzeichenwechsel von + nach -. An der Stelle x = 1 ist also ein relatives Maximum.
Wenn x > 3 ist, sind beide Faktoren positiv, f'(x) also auch. Also ist hier ein Vorzeichenwechsel von – nach +. An der Stelle x = 3 ist also ein relatives Minimum.
Zuletzt setzen wir die x-Werte der Extremwerte in f(x) ein:
f(1) = 2 Das relative Maximum ist also H(1|2)
f(3)= -2 Das relative Minimum ist also T (3|-2)
Hier die Graphen dazu:
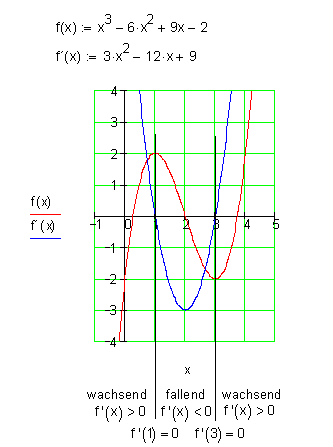
Dazu kannst du die das 📽️ Video Extrempunkte in der Differentialrechnug ansehen.
Bedingungen um Extrempunkte zu berechnen
Die Bedingung für eine waagerechte Tangente f'(x) = 0 ist eine notwendige Bedingung für das Vorhandensein eines Extrempunktes. Aber das ist dafür nicht hinreichend.
Denn erst der Nachweis über einen Vorzeichenwechsel liefert eine hinreichende Bedingung und kennzeichnet den Extrempunkt als rel. Min. oder als rel. Max.
Beispiel:

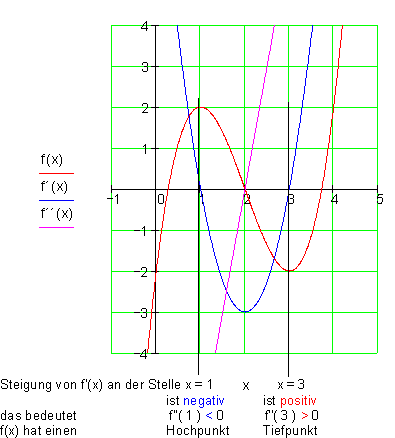
2. Nachweis für Extrempunkte mit Hilfe der zweiten Ableitung von f(x)
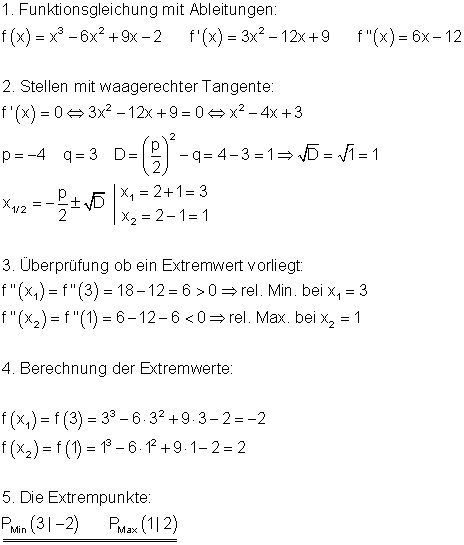
Dazu könnt ihr euch das 📽️ Video Extrempunkte hinreichende Bedingung ansehen.
Zusammenfassung: Extrempunkte berechnen

2. Nachweis auf Hochpunkt (rel. Max.) bzw. Tiefpunkt (rel. Min.)

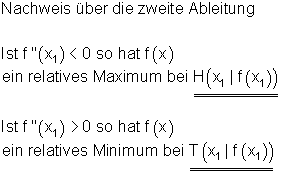
3. Einsetzen der x – Werte in f(x) liefert die Funktionswerte (y – Werte) der Extrempunkte.
Nachweis über die zweite Ableitung
Der Nachweis über die zweite Ableitung ist in den meisten Fällen der einfachste Weg zum Auffinden der Extrempunkte.
Fassen wir die Bedingungen für Extrempunkte zusammen:
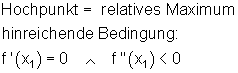

Extremwerte berechnen kommentierte Beispiele
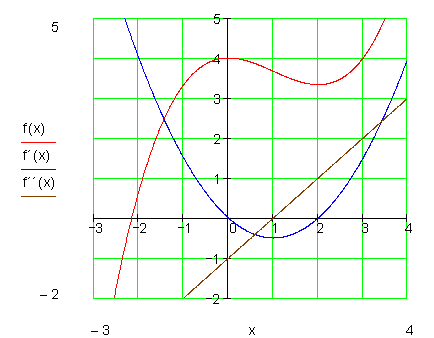
Beispiel 1 Extremwerte berechnen:
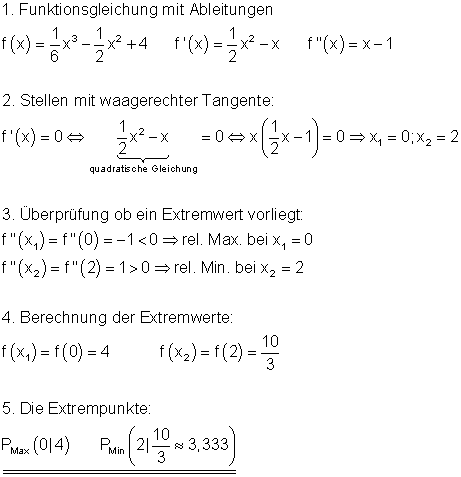
Beispiel 2 Extremwerte berechnen:
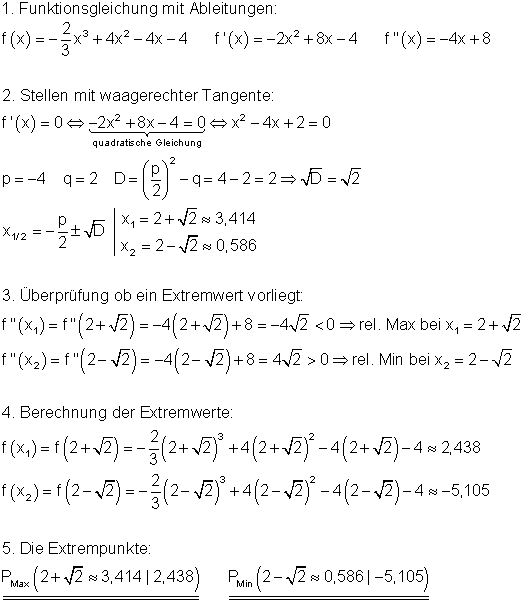
Genauigkeit beim Extremwerte berechnen:
Zur Bestimmung der Extremwerte sind die Werte der Extremstellen möglichst genau in die Funktionsgleichung einzusetzen.
Um Punkte in ein Koordinatensystem zu zeichnen, reicht jedoch eine Genauigkeit von 2 Stellen hinter dem Komma aus.
Notwendige Bedingung, hinreichende Bedingung
Svenja möchte selbst mit dem Auto zur Schule fahren.
Eine notwendige Bedingung ist, dass sie eine gültige Fahrerlaubnis hat.
Das allein reicht aber nicht aus, sie benötigt auch ein Auto.
Herr Meier hat einen gültigen Führerschein.
In seiner Garage stehen zwei betankte und zugelassene Autos, die ihm gehören.
Dieser Sachverhalt ist hinreichend dafür, dass Herr Meier als Fahrer agiert.
Aber zwei eigene Autos müssen nicht sein.
Petra hat auch einen Führerschein, ihr steht ein fahrbereites, zugelassenes Auto zur Verfügung.
Diese Bedingung ist notwendig und hinreichend, Petra darf also unbesorgt fahren.
Hier findest du Trainingsaufgaben dazu.
Relative und absolute Extrema
Bislang sprachen wir nur von einem relativen Minimum, bzw. von einem relativen Maximum. Diese Extrema sind lokal.
Wir betrachten nun eine Funktion auf ihrem maximalen Definitionsbereich D = IR.
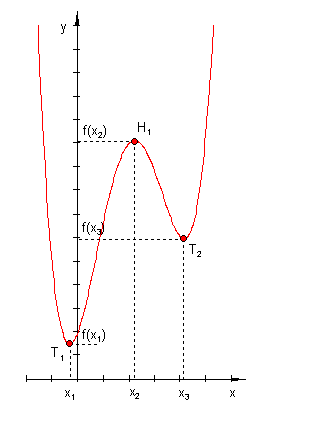

Das Verhalten der Funktionswerte für immer kleiner werdende x-Werte, bzw. für immer größer werdende x-Werte soll nun betrachtet werden.
Für immer kleiner werdende x-Werte werden die Funktionswerte immer größer, gleiches gilt auch für immer größer werdende x-Werte. Wir schreiben:![]()
Ist die gleiche Funktion auf einem Intervall D = [ a ; b ] definiert, dann gilt:
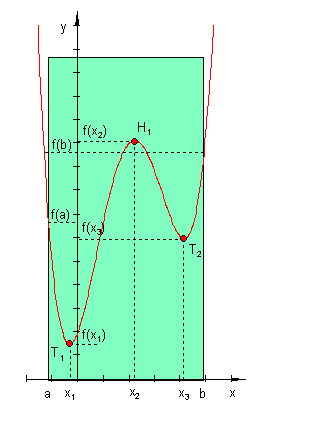

Liegt als Definitionsmenge ein Intervall vor, so sind die Funktionswerte auch an den Randstellen zu untersuchen.
Definitionen relatives und absolutes Extremum:
Ist f ( x0 ) der größte oder kleinste Funktionswert in einer Umgebung von x0 , so ist f ( x0 ) ein relatives Extremum.
Ist f ( x0 ) der größte oder der kleinste Funktionswert innerhalb des Definitionsbereichs, so ist f ( x0 ) ein absolutes Extremum.


